線性電路分析——網孔法詳析
一. 定義
由人們主觀設想的在網孔中流動的電流稱為網孔電流,如圖3-3-1中的iⅠ,iⅡ,iⅢ所示,它們的大小和參考方向均是任意設定的。以網孔電流為待求變量,根據KVL對各網孔列寫出KVL約束方程而對電路進行分析的方法稱為網孔電流法,簡稱網孔法。
二. 網孔電流變量的完備性與獨立性
網孔電流變量的完備性是指電路中所有的支路電流都可由網孔電流求得。設各支路電流的大小和參考方向如圖3-3-1中所示。若認為各網孔電流已被求出,則可得各支路電流為:


網孔電流變量的獨立性是指各網孔電流之間不受KCL約束,彼此獨立,不能互求。例如對于節點a,我們可列出方程:
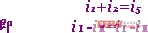
此式為一恒等式,即不管網孔電流iⅠ,iⅡ為何值都恒成立。對于其他節點也能得到類似結果,所以網孔電流變量具有獨立性。
由于網孔電流變量具有完備性與獨立性,所以可作為電路分析的變量。
三. 網孔KVL約束方程的列寫與求解
在列寫網孔的KVL約束方程時,應首先設定網孔電流的大小和參考方向。為了使所列方程有規律和容易寫出,一般設定網孔電流的參考方向都是均為順時針或均為逆時針,而且回路的循行方向就取為與網孔電流的參考方向一致。顯然,網孔電流的個數以及所列KVL約束方程的個數,都一定是等于網孔數。例如對于圖3-3-1所示電路可列出如下方程:
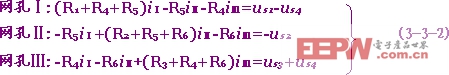
此方程稱為網孔電壓方程,簡稱網孔方程。解之即得各網孔電流iⅠ,iⅡ,iⅢ.
在上式中,令R11=R1+R4+R5,R22=R2+R5+R6,R33=R3+R4+R6,它們分別為網孔Ⅰ,網孔Ⅱ,網孔Ⅲ的自電阻,恒為正值;令R12=R21=-R5,R13=R31=-R4,R23=R32=-R6;R12,R21均稱為網孔Ⅱ與網孔Ⅲ的互電阻。若設定網孔電流的參考方向均為同一方向(同為順時針方向或同為逆時針方向),則互電阻均為負值,式(3-3-2)中即屬此種情況;若設定網孔電流的參考方向不是均為同一方向(即有順時針方向,有的為反時針方向),則互電阻中有的為正值,有的則為負值(若流過負電阻的相鄰兩個網孔電流的方向相同,則互電阻前取+號,否則取-號)。令us11= us1-us4,us22=-us2,us33= us3+us4,它們分別為網孔Ⅰ,網孔Ⅱ,網孔Ⅲ的所有電源電壓升高的代數和。這樣式(3-3-2)即可寫為

可見網孔方程的列寫是很有規律的。將上式寫成矩陣形式即為
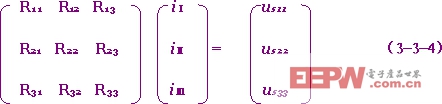
或 RiM=uM (3-3-5)

稱為網孔電阻矩陣,為一對稱陣:
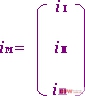
稱為網孔電流列向亮:
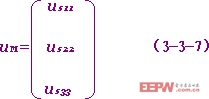
稱為網孔電壓源電壓列向量。式(3-3-4)或(3-3-5)即為矩陣形式的網孔方程。求解式(3-3-5)即得:iM= R‾¹uM (3-3-8)
四.支路電流與支路電壓的求解
將所求得的iⅠ,iⅡ,iⅢ代入式(3-3-1),即可求得各支路電流,進一步又可根據支路的伏安關系求得各支路電壓為

(1).畫出電路圖。
(2).設定各網孔電流的大小和參考方向,其參考方向一般都取為同一方向,即同為順時針方向或同為逆時針方向。
(3).對各網孔KVL約束方程,方程個數與網孔個數相等。
(4).聯立求解KVL約束方程組,即可得各網孔電流。
(5).設定各支路電流的大小和參考方向,根據所求得的網孔電流,即可求出各支路電流和各支路電壓,并進一步求出支路功率。至此,求解工作即告完畢。
例3-3-1 求圖3-3-2所示電路的各支路電流和支路電壓。
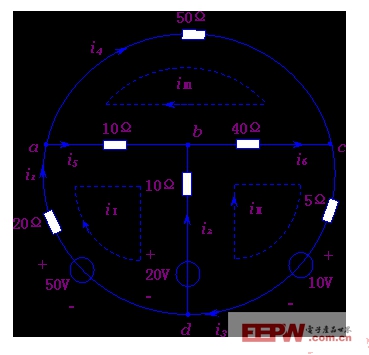
圖3-3-2 例3-3-1的電路
解:該電路的支路數b=6,網孔數l=3。設各網孔電流的大小和參考方向如圖中所示。于是可列出網孔的KVL方程為:

寫成矩陣形式為

解之得:iⅠ=0.99A,iⅡ=0.61A,iⅢ=0.34A
設各支路電流的大小和參考方向如圖中所示,故得:
i1=iⅠ=0.99A
i2=iⅡ-iⅠ=-0.38A
i3=iⅡ=0.61A
i4=iⅢ=0.34A
i5=iⅠ-iⅢ=0.65A
i6=iⅡ-iⅢ=0.27A
進一步可求得各支路電壓為:
uab=10i5=6.5V
uad=-20i1+50=30.2V
uac=50i4=17V
ubd=-10i2+20=23.8V
ucd=5i3+10=13.05V
ubc=40i6=10.8V
當支路電流與支路電壓求得后,即可很容易地求得各支路的功率。例如支路bd吸收的功率為Pbd=ubd(-i2)=23.8×0.38=9.04W,支路ad發出的功率為:Pad=uadi1=30.2×0.99=29.9W.



評論