線性電路分析——節點法詳析

一． 定義
以獨立節點電位為待求變量，根據KCL對各獨立節點KCL約束方程，而對電路進行分析的方法稱為節點電位法，簡稱節點法。獨立方程的個數等于獨立節點的個數，即(n-1)個。非獨立節點的電位取零，稱為參考節點，也稱接地，并用符號┴ 。節點法對平面網絡與立體網絡均適用。 二． 獨立節點電位變量的完備性與獨立性
獨立節點電位變量的完備性是指電路中所有的支路電壓，都可由獨立節點電位求得。例如圖3-5-1所示電路，它有四個節點，五個支路電流。對四個節點進行編號如圖中所示，并取節點(1)(2)(3)(4)為參考節點，即取節點(4)的電位φ4=0，則節點(1),(2),(3)即為獨立節點。設它們的電位分別為φ1，φ2，φ3。今若φ1，φ2，φ3已知，則各支路電壓即均可求得為：

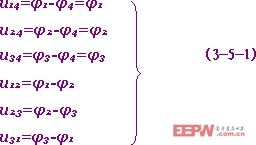
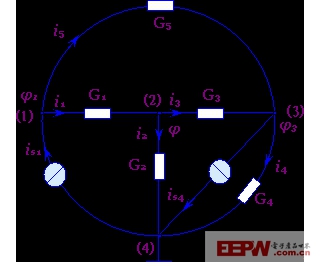
圖3-5-1 節點法 可見獨立節點電位變量具有完備性。
獨立節點電位變量的獨立性是指各獨立節點電位之間不受KVL約束，彼此獨立，不能互求。例如對外網孔回路，我們可KVL方程
即 　　　　　φ1-φ3+φ3-φ4+φ4-φ1=0
即　　　　　　0=0
此式恒為一等式，即不管φ2, φ3, φ4為何值都恒成立。對其它回路也能得到同樣結果。所以，獨立節點電位變量具有獨立性。
由于獨立節點電位變量具有完備性與獨立性，所以可作為電路分析的變量。
三． 獨立節點KCL約束方程的列寫與求解
在圖3-5-1所示電路中，設各支路電流的大小和參考方向如圖中所示。于是對三個獨立節點可列出方程：
此方程組稱為獨立節點電流約束方程，簡稱節點方程。解此方程組即可得各獨立節點電位φ1，φ2，φ3。
在式（3-5-4）中，令G11=G1+G5，G22=G1+G2+G3，G33=G3+G4+G5，它們分別為節點(1)，(2)，(3)的自電導，為正值；令G12=G21=-G1，G13=G31=-G5，G23=G32=-G3;G12，G21均稱為節點(1)與節點(2) 互電導，G13，G31均稱為節點(1)與節點(3)的互電導，G23，G32均稱為節點(2)與節點(3)的互電導。互電導為負值。令is11= is1，is22=0，is33=- is4，它們分別為流入各該節點的電流源電流的代數和，流入節點者取+號，流出節點者取-號。這樣式（3-5-4）即可寫為

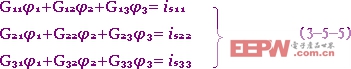
可見節點方程的列寫也是很有規律的。
將上式寫成矩陣形式即為：

即 GΦ=in （3-5-7）

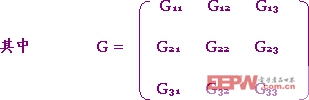
稱為節點電導矩陣，為一對稱陣：

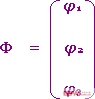
為獨立節點電位列向量；

為節點電流源電流列向量。式（3-5-6）或（3-5-7）即為矩陣形式的節點方程。 求解式（3-5-7）得： Φ=G‾¹in （3-5-8）

四． 支路電壓與支路電流的求解
將所求得的φ1，φ2，φ3代入式（3-5-1）即可求得各支路電壓。在求支路電流時，同樣應先設定它們的大小和參考方向橫。若設定4各支路電流的大小和參考方向如圖3-5-1中所示，則即可根據式（3-5-3）求得各支路電流。
五． 節點法的一般步驟
（1）.畫出電路圖。
（2）.選取參考節點，并設定各獨立節點電位的大小和正負性，一般都是取各獨立節點為+極端，參考接點為-極端。
（3）.對各獨立節點列寫KCL約束方程，方程個數與獨立節點個數相等。
（4）.聯立求解KCL約束方程組，即可得各獨立節點電位。
（5）.設定各支路電流的大小和參考方向，根據所求得的獨立節點電位，即可求得各支路電壓和支路電流。至此，求解工作即告完畢。
最后要指出的是，節點法的應用極為廣泛。這是因為：（1）它既適用與平面網絡，也適用與非平面網絡；（2）在實際電路中，其獨立節點數往往要比網孔數少。
例3-5-1 列出圖3-5-3（a）所示電路的節點方程并求解

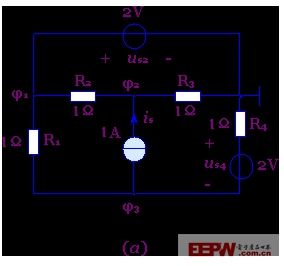
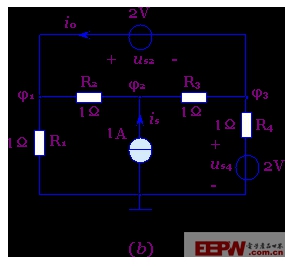
圖3-5-3 例3-5-1的電路

解：該電路的特點是在其中的兩個節點之間有一2V的理想電流源，無法將它等效變換為電流源。對與此種電路，若選電壓源的一端（例如負端）作為參考接點，則電壓源另一端的電位即為已知，即φ1=2V
這樣，該電路就只有兩個未知的節點電位φ2和φ3。對應的節點方程為

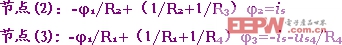
代入數據，聯立求解以上三式即得 φ1 =2V，φ2=1.5V, φ3=0.5V.
但若選參考節點如圖3-5-3(b)所示，則由于三個獨立節點電位φ1，φ2，φ3均為未知，故必須對三個對立節點列出方程，且應設定流過電壓源中的電流大小為i0與參考方向，如圖3-5-3（b）中所示。于是可列出方程為

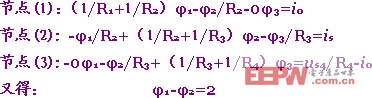
聯解得 1=2.5V,φ2=2V, φ3=0.5V, i0=3A.