大型超精密平面度在線測量與誤差補償技術
加入技術交流群
對于平面度在線測量，可以采用四測頭電容式組合傳感器裝置安裝在加工機床的z軸上，按一定的測量走點路徑對工件表面進行測量，測量結果中迭加了兩項誤差：基準誤差(即導軌運動副誤差)和工件表面誤差。因此，要精確測量工件平面度，必須采用誤差分離技術。
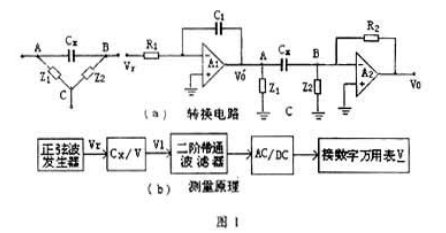
對平面度在線測量可以采用三或四傳感器進行。其中三傳感器布置方式如圖1所示。傳感器邊距為L，這樣以 L長為間隔可將被測平面分為M行N列網格，處于網格上的點即為被測量點，三傳感器分別標記為(k，l)(k，l＝1，2)，對應第i行j列上的測量點標記為(i，j)。以傳感器(l，l)的零點作為基準點。則傳感器(1，2)、(2，1)的初始位置偏差分別記為）Δ12、Δ21。
對于平面度形狀誤差的誤差分離方法，可以采用遞推逐次兩點(TSTP)法和最小二乘逐次兩點(LSSTP)法。對于大型精密、超精密平面度在線測量，則應采用混合逐次兩點(HSTP)法，對于精密小平面工件，采用二維最小二乘插值逐次兩點(LSISTP)法進行誤差分離，
2．1測量誤差源分析
逐次兩點誤差分離方法是以采樣公式(1)為分析處理基礎的，但在實際系統中，由于各種因素的影響，采樣獲得的傳感器信息中不僅包含運動副誤差和測量平面形狀誤差，而且還帶有各種噪聲信號。理論分析和實驗研究情況表明，影響采樣數據的誤差源很多，如漂移誤差、隨機噪聲誤差、采樣量化誤差、擺角誤差、各種低頻振動、導軌運動不平穩等。對于大型 CNC超精密平面磨床而言，影響在線測量系統精度的因素主要有以下，幾項：漂移誤差、隨機噪聲誤差、傳感器電源及導軌氣源波動、機床振動。
由于環境條件等的緩慢變化引起傳感器中頻漂移，尤其對于大工件測量時所需時間較長，漂移誤差的影響更大。但理論研究及分析表明：若傳感器漂移曲線相同，則漂移誤差影響可以通過分離處理消除，這樣在設計制作傳感器時盡量保證傳感器的特性相近，則環境變化對傳感器的影響基本相同，漂移誤差的影響得到抑制。
在線測量的環境不能算太好，采樣測量中不可避免存在各種各樣的干擾，‘如振動、電磁干擾、導軌運動的不平穩、傳感器電路不穩定等等，都會使得采樣值中存在隨機噪聲誤差。通過幾種算法處理過程可以發現：采用最小二乘處理進行誤差分離的辦法可以減少隨機噪聲的影響。
傳感器電源紋波、導軌氣源波動和機床振動都會對傳感器采樣值產生影響，因此需要分別采取措施減少影響。另一方面，由于其作用對幾個傳感器是相同的，因此誤差分離處理時，它們只影響導軌分離精度，而對工件表面分離結果沒有影響。
2.2 實用誤差分離方法的討論
對于平面度形狀誤差在線測量，可以采用TSTP法、LSSTP法、HSTP法、ILSSTP法等。其中TSTP法具有處理過程簡單、速度快的特點，但該方法的分離結果容易積累測量噪聲誤差，特別是大型工件在線測量的場合，分離精度較低：LSSTP法則可以抑制隨機噪聲的影響，得到更高精度的測量結果，該方法將多項誤差通過一次處理得到，這樣可能因為誤差均化而導致分離結果不準確。對于大型平面測量，由于處理矩陣太大而使得算法實現非常困難且可能導致浮點運算誤差。HSTP法實現了單項誤差分離處理，它以TSTP方法得到的結果作為初始值通過共軛梯度法迭代逼近可以實現大型平面快速精確的誤差分離。該方法避免了LSSTP方法可能產生的誤差均化及浮點運算誤差p大型超精密平面度測量采用該方法最為合適。這三種方法的測量間隔等于測頭間距而不能變更，這樣對于中小型平面測量會導致測量結果不夠精確。ILSSTP法可以實現以小于測頭間距的間隔進行測量并抑制隨機噪聲的影響，當測量點較多時也可以采用共軛梯度迭代逼近的辦法得到精確的分離結果。作為ILSSTP法的特例，對于直線度在線測量同樣可以通過最小二乘處理得到高精度分離結果。
3 平面度評價方法
目前對平面度的評估主要有四種方法：方格法、對角線法、最小二乘法和最小包容區域法。前兩種方法處理比較簡單，在工程現場上應用較多，但其結果存在偏差。最小二乘法也是一種簡單快捷的近似評估方法，易于計算機編程實現，其評估結果誤差相對較小。最小區域法符合國標規定的最小條件原則，其評估結果唯一且比前幾種方法都精確，故而最受重視，其實現相對較為復雜，很多學者采用了各種不同算法來實現該方法。在進行最小區域法實現時，各種文獻提供了數十種求解算法，常用的有基面旋轉法、坐標變換法、優化法、特征點法和作圖法等，這些算法都有各自的優點。但對于大型超精平面測量處理而言，數據點太多。對如此多的數據點進行反復處理，前面提供的算法效率都太低，處理時間太長。針對這種情況，我們提出了一種對數據預處理的計算機算法，大大提高了處理效率。
算法的主要思路是通過優化搜索序列、通過置換法尋找特征點、用判別準則進行驗證、再循環搜索、直到得到滿足條件的特征點為止。為提高搜索速度，綜合幾種方法的優點，采取了最小二乘預處理、分組設定優先順序、選定搜索方向等多條優化措施。 電容傳感器相關文章:電容傳感器原理
評論