綜合布線中的兩個概念問題

三、實際應用

通信系統的帶寬表示了其傳輸這些不同頻率組件的能力。在結構化布線系統中帶寬的單位通常以MHz 表示。超五類布線的帶寬名義上有1 0 0MHz。假設應用一個簡單的二進制傳輸“碼”，那么在理論上，可以由Nyquist(奈奎斯特)等式來計算最大的信息傳輸率：C= 2 W Log 2 M
其中，W 為帶寬（單位：H z ），M 為信令單元的數量,當M=2時, C= 2 W。

這就得出理論信息容量為每秒2x108 比特,即200Mbps。實際上，由于串擾和衰減的影響這個值會有所減少。

那么，超五類信息道支持數據傳輸達到千兆位以太網（1 0 0 0Mbps），如何讓帶寬適合于它呢？那就得增加數據傳輸率，增加數據吞吐量的關鍵，是對每個信令單元引入多于1 比特。商業運用中大部分公共協議都在某種程度上用到了這種技術，我們稱之為數據編碼。

大部分數據編碼類型都利用mBnL編碼來實現，也就是由L個電平每個電平n個脈沖來表示m比特的序列。使用實例如ISDN 和快速以太網。以100Base-T4 為例。100 Mbps信號分成三線對進行傳輸。每線對的比特率為33.33 Mbps。為了減少該比特流的頻率容量以及布線系統的帶寬需求，就要運用三重代碼。在傳輸各組8 比特數據之前，轉換為6 個三重符號（見圖3 ）。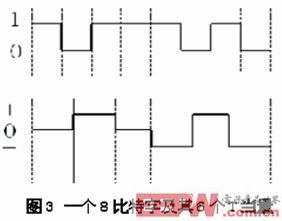

這就把發送信號系統的有效時鐘速率減少至2 5 M H z，這樣（在我們所述的第一個例子中）基頻減少至12.5 MHz。這允許三類布線系統中提供的帶寬內傳輸率為100 Mbps。

千兆位以太網采用了一種不同的方案，它把各組8 比特（8 B）數據轉換為穿過四根雙絞線的四個五重符號（1 Q 4）的傳輸, 每個符號代表兩個二進制比特或零。即使用PAM-5編碼,它使用-2,-1,0,1,2五種電平,其中四個電平用戶信號編碼,一個電平用于向前糾錯編碼。五級PAM編碼相對于二進制編碼將信道利用率提高了一倍,這樣每線對的信號波特率下降為125MB/s,則基帶將為62.5MHz,再一次降低了信號所占用的帶寬.這樣確保超五類系統滿足帶寬需求。

四、結論

各個應用的比特率與其基頻有關。最高的頻率容量是基頻的諧波。不應把它與時鐘頻率相混淆（比特流以時鐘頻率取樣）。例如，10Base-T 的比特率為10Mbps，采樣時鐘為10MHz，但是基頻僅為5 MHz。通過以MHz 表示系統性能需求，標準提供了一個藍圖，有源網絡組件設計人員都可以根據它來設計他們的設備。提供的布線系統和有源設備都滿足相關標準的性能需求，那么所有的一切都正常運轉起來！作為用戶，最感興趣的是通信速率。速率是從應用層次對通信作出描述的。為提高通信速率，有兩個途徑可以考慮：一個是提 高線纜系統的傳輸性能，由此決定了帶寬；另一個是選擇合適的編碼系統，從而決定了轉換因子。 盡管帶寬在物理上受到限制，但是通過合適的編碼系統可以獲得更高的通信速率。尤其需要指出的是，編碼系統是依賴于應用的，這意味著一個具有相同位流速率但采用不同編碼方式的新應用，并不一定能得到原系統的支持，所以在設計的時候，如果僅僅考慮那些支持目前已有應用系統的布線組件，并且選擇位流速率MHz來描述的話，那么這將導致嚴重錯誤的決策。從這個角度來說，任何一個開放系統都應該獨立于應用。而且只有使用MHz來描述通信速率，我們才能從當前以及未來廣闊應用領域之中作出充分的選擇。對于綜合布線系統的性能定級問題，我們只能用帶寬而不能用速率進行衡量

附：

奈氏準則與香農公式

奈氏準則

1924年，奈奎斯特（Nyquist）就推導出在理想低通信道下的最高碼元傳輸速率的公式：

理想低通信道下的最高碼元傳輸速率＝2W Baud

其中W是理想低通信道的帶寬，單位為赫茲；Baud是波特，即碼元傳輸速率的單位，1波特為每秒傳送1個碼元。奈氏準則的另一種表達方法是：每赫茲帶寬的理想低通信道的最高碼元傳輸速率是每秒2個碼元。若碼元的傳輸速率超過了奈氏準則所給出的數值，則將出現碼元之間的互相干擾，以致在接收端就無法正確判定碼元是1還是0。

對于具有理想帶通矩形特性的信道（帶寬為W），奈氏準則就變為：理想帶通信道的最高碼元傳輸速率＝1W Baud，即每赫寬帶的帶通信道的最高碼元傳輸速率為每秒1個碼元。

奈氏準則是在理想條件下推導出的。在實際條件下，最高碼元傳輸速率要比理想條件下得出的數值還要小些。電信技術人員的任務就是要在實際條件下，尋找出較好的傳輸碼元波形，將比特轉換為較為合適的傳輸信號。需要注意的是，奈氏準則并沒有對信息傳輸速率（b/s）給出限制。要提高信息傳輸速率就必須使每一個傳輸的碼元能夠代表許多個比特的信息。這就需要有很好的編碼技術。

香農公式

1948年，香農（Shannon）用信息論的理論推導出了帶寬受限且有噪聲干擾的信道的極限信息傳輸速率。當用次速率進行傳輸時，可以做到不出差錯。用公式表示，則信道的極限信息傳輸速率C可表達為C＝B log2（1+S/N） 信噪比SNR = S(信號功率) / N (噪聲功率)

其中B為信道的寬度，S為信道內所傳信號的平均功率，N為信道內部的噪聲功率。

香農公式表明，信道的帶寬或信道中的信噪比越大，則信息的極限傳輸速率就越高。它給出了信息傳輸速率的極限，即對于一定的傳輸帶寬（以赫茲為單位）和一定的信噪比，信息傳輸速率的上限就確定了。這個極限是不能夠突破的。要想提高信息的傳輸速率，或者必須設法提高傳輸線路的帶寬，或者必須設法提高所傳信號的信噪比，此外沒有其他任何辦法。至少到現在為止，還沒有聽說有誰能夠突破香農公式給出的信息傳輸速率的極限。香農公式告訴我們，若要得到無限大的信息傳輸速率，只有兩個辦法：要么使用無限大的傳輸帶寬（這顯然不可能），要么使信號的信噪比為無限大，即采用沒有噪聲的傳輸信道或使用無限大的發送功率。