基于DSP與FPGA的光柵地震檢波器的信號處理系統

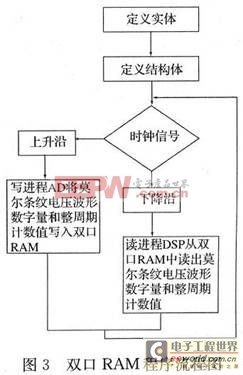
2．3 雙口RAM的仿真結果

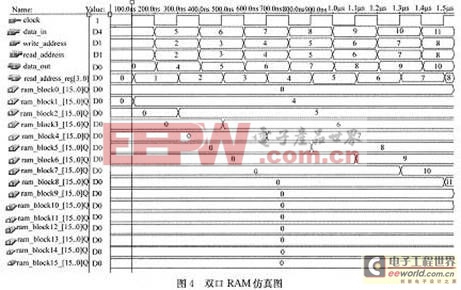
圖4為該進程的仿真時序圖，由圖可見第一個時鐘的上升沿數據輸入端口data_in的值為4，這時寫選通端口write_address選通地址1，然后對應著地址1的存儲器模塊ram_block1的內的值在此刻刷新為4，這說明寫進程正確。同時應注意到讀地址選通信號read_address的值被傳遞到讀地址寄存器read_address_reg中，read_address_reg中的值被刷新為1。當第一個時鐘的下降沿到來時，信號輸出端口data_out根據讀地址寄存器read_address_reg中的地址值1選通ram_block1，此時data_out的值刷新為4，這說明讀進程也正確。

3 DSP的軟件細分

采用大數可逆計數與小數細分計數的軟件細分技術。其中大數計數是對莫爾條紋整周期數進行可逆的加減計數，這部分功能有采集模塊中的FPGA來完成，小數計數是對莫爾條紋不到一個周期信號細分結果進行計數，其功能由DSP來完成。運算的結果為大數計數結果乘以光柵柵距與小數計數結果乘以細分當量之和，其中細分當量為光柵柵距除以細分倍數。該模塊的硬件原理圖如圖5所示。

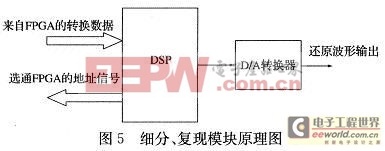
通過DSP的地址選通線依次選通讀取FPGA中三個數據緩存區中的數據，緩存區分別存放兩路模擬信號的數字量與加減計數器的累加計數值，然后利用公式R=N*w+K*L求出任意一點諧振子的幅值并輸出。式中N為整周期的累加計數值，W為光柵柵距，K為細分計數，L=W／M，M為細分倍數。該細分模塊主要是完成對細分計數K值、和幅值R值的求取，并完成對幅值的數字量轉換并輸出。

其中細分方法也就是對K值的求取采用了八卦限幅值分割法，根據上述方法設計了細分倍數可變的細分算法，利用DSP C語言的專用庫函數實現了純計算的算法。細分算法流程如圖6所示。

由幅值細分法可知，軟件細分算法設計的關鍵問題是根據兩路信號的比值對該點的相位角的正確定位。該點的位置有兩種情況，一種是落在各象限的邊界上，另一種是落在各象限之中。根據細分邊界條件判斷該點的采樣數據是否發生在四個象限的分界線上，如果判斷此次換向發生在象限的分界線上，則細分數為固定值，并且通過象限的正負關系就可以確定具體細分數值，不需要進行復雜的計算。如果該點不是發生在象限分界線上，則需根據象限正負關系判斷換向發生的具體象限，不同象限對應不同計算公式。細分算法程序如下：

根據標志字判斷相位點的位置，根據相應位置不同公式求取細分值

然后利用公式R=N×ω+d×L求出任意一點諧振子的幅值并輸出。式中N為整周期的累加計數值，W為光柵柵距，d為細分計數，L=ω／m，m為細分倍數。

4 結束語

設計的光柵地震檢波器充分結合了FPGA的強大控制功能和DSP高速運算處理功能，實現了信號的同步采集、高倍細分和實時復現。減少了單一處理器的負荷，提高了系統的速度和穩定性，為光柵震動信號處理提出了一個新思路。由于硬件雙口RAM接口時序復雜，成本高也會給系統帶來不穩定性，因此本文在FPGA中設計了一軟RAM。對于振動信號幅值的計算則是在對整周期的莫爾條紋進行計數的同時，利用軟件細分法實時地計算出非整周期的莫爾條紋信號所代表的小數值，并實時將二者相加后乘以莫爾條紋當量(每個莫爾條紋所代表的位移量)，即可得到信號的實時振動幅值。