DC-DC變換器非線性混沌現象研究
1 引言
DC-DC變換器是開關電源的核心技術,實際運行中常常會出現一些奇異或不規則現象,諸如臨界運行的突然崩潰、不明的電磁噪聲、控制系統的間歇振蕩、系統運行的不穩定和系統無法按設計要求工作等等。這些現象由來已久,然而長期以來人們都把它們歸納為系統故障和外界隨機干擾,影響了DC-DC變換器的研究、設計和開發,使得DC-DC變換器性能的提高受到極大的限制。
眾所周知,DC-DC變換器是一個固有開關非線性系統,因此變換器運行必然遵循非線性運行規律。現有的研究表明已被觀察到DC-DC變換器的奇異或不規則現象是一些典型的混沌現象 [1]。顯然當DC-DC變換器工作在混沌狀態時,混沌運動的貌似隨機性將導致系統的運行狀態無法預測,使DC-DC功率變換器的控制性能受到極大的影響,甚至完全不能工作。因而突破現有在線性范圍內或穩定運行區域內研究DC-DC變換器的局限性,從非線性系統混沌理論的高度探索DC-DC變換器的運行規律,對有效地提高DC-DC變換器運行性能,具有重大的理論和實際意義。
通過對各種DC-DC變換器的混沌現象探索和研究,可以達到如下重要的目的:(1)在變換器設計中優化參數設計,避免有害混沌現象的出現,消除奇異或不規則現象,使DC-DC變換器穩定運行;(2)由于混沌運動中存在很多不穩定的周期軌道,可以采用混沌控制技術,控制DC-DC變換器工作在預期的周期軌道上,從而實現周期軌道的快速變換,使DC-DC變換器的工作性能超常規的提高;(3)利用DC-DC變換器的混沌特性實現常規控制難以實現的技術,如利用混沌功率譜特性降低DC-DC變換器中的電磁干擾、利用混沌同步特性實現DC-DC變換器的均流技術、利用混沌運動的初值敏感性提高DC-DC變換器的動態響應特性等。
為此本文將在簡要介紹非線性混沌理論基礎上,歸納DC-DC變換器混沌運動的基本類型,總結現有DC-DC變換器混沌運動的研究方法,綜合DC-DC變換器混沌現象的抑制或控制技術,提出非線性混沌運動在DC-DC變換器應用的研究思路。
2 DC-DC變換器中的混沌現象
長期以來,對客觀事物運動規律的描述,一直采用確定論和概率論兩種體系,確定論的基礎是牛頓力學,用以描述事物的確定性運動;而概率論的基礎是統計學,用以描述事物的隨機運動,代表性的成果是量子力學。確定性運動和隨機運動被認為是涇渭分明、毫無關系的兩種類型的運動,確定性運動可以用確定性方程所描述,隨機運動只能用統計學規律所描述,沒有人懷疑它們之間存在由此及彼的關系。直到上世紀60年代初,美國氣象學家Lorenz在對大氣對流模型作數值計算時,首先發現了耗散系統中的混沌運動,即發現確定性系統可以產生類似隨機的運動,從而使人們有理由認為許多以往被視為隨機的運動可能是由確定性系統所產生,確定性運動與隨機運動可能存在某種必然的聯系,存在由此及彼的關系。因而混沌運動也被視為上一世紀自相對論和量子力學的第三大重大發現,Lorenz也成為第一個針對現實物理系統進行混沌研究的科學家。
混沌運動的發現,使人們開始重新審視以往許多已被定論的研究成果,幾乎涉及各個科學研究領域,都在證實確定性運動與隨機運動的關系,取得了許多重大的研究成果,澄清了許多重大現象的實際產生原因,并應用混沌特性實現了許多常規定律無法取得工作特性。然而令人遺憾的是對電力電子系統混沌現象的研究,直到上個世紀90年代初才開始引起少數學者的關注,但至今還主要停留在對DC-DC變換器混沌運動的研究上。究其原因,一是電力電子系統本身的非線性復雜性,建立其分析模型十分困難;二是電力電子系統自身還處在一個發展時期,由于其強的應用性,許多基本的問題未得到有效的關注,從而未被解決;三是電力電子系統研究思路,大多還局限于拓撲結構的研究上,以及實際應用上,研究思路尚未轉變;四是電力電子系統研究方法上,仍采用傳統的電路分析理論,對其它新科學理論不夠敏感;五是非線性混沌理論自身仍處在一個完善和發展時期。因而使得對電力電子系統混沌運動的研究處于起步階段,也沒有引起人們廣泛的關注和興趣。
盡管如此,對DC-DC變換器混沌運動的研究也以取得重要的成果,其中對DC-DC變換器混沌運動的基本類型已有深入的了解,歸納起來,DC-DC變換器混沌運動有以下基本類型:
1、 倍周期分岔混沌運動
倍周期分岔是DC-DC變換器最常見和基本的一種現象,其特性表現為隨著變換器參數的變化,系統運動規律從周期運動轉變為倍周期運動,然后進入混沌運動。Buck變換器以及電流模式控制下的Boost變換器都會出現倍周期分岔的混沌運動。
2、 Hopf分岔混沌運動
Hopf分岔混沌運動是指DC-DC變換器隨參數變化,由穩定不動點轉換為周期振蕩直至混沌的DC-DC變換器混沌現象。電壓模式控制下的Boost變換器、電流模式控制下的Cuk變換器都可以產生Hopf分岔混沌運動。
3、 準周期分岔混沌運動
準周期分岔混沌運動是指DC-DC變換器隨參數變化,出現以某個頻率為基生成的一系列周期運動的疊加運動,并由此使DC-DC變換器進入混沌狀態的現象。PWM電壓模式控制下的Boost變換器以及DC-DC變換器開環控制在外施正弦擾動激發下、閉環DC-DC變換器在反饋參數的變化下可以產生準周期分岔混沌運動。
4、 邊界碰撞分岔混沌運動
邊界碰撞分岔混沌運動是指DC-DC變換器,從某個周期狀態突然跳躍混沌狀態。Buck變換器以及電流模式控制下的Boost變換器以及積分電流反饋控制的Buck變換器,在一定參數條件下都可以發生邊界碰撞分岔混沌運動。
[next]3 DC-DC變換器混沌現象的研究方法
3.1建模方法
DC-DC變換器有六種基本形式,其中進行混沌現象研究較多的是buck、boost變換器和 變換器。由于以往的發展起來的大信號模型和小信號模型不適合于非線性現象的研究,因而不同階數DC-DC變換器混沌建模就成為它們混沌現象研究最重要的內容。
3.1 .1一階系統
當Buck和Boost變換器的負載是恒壓源;或者當與負載并聯的電容C足夠大時;或者當Buck和Boost變換器處于不連續工作模態時,Buck和Boost變換器的數學模型就可以用一階狀態方程表示。
Hamill和Jeffries首先對DC-DC變換器的混沌現象進行了理論分析。文中的研究對象是電流型PWM Buck變換器,它以恒壓源為負載,電路工作于連續模態。由系統的一階狀態方程推導出續流電感L上的電流迭代式 :
: 。其中D是功率開關管的占空比,
。其中D是功率開關管的占空比,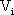 和
和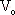 分別是變換器的輸入電壓和輸出電壓。根據上述迭代式,用計算機仿真得出系統主要變量的相圖,顯示了系統由倍周期分岔通向混沌的道路。
分別是變換器的輸入電壓和輸出電壓。根據上述迭代式,用計算機仿真得出系統主要變量的相圖,顯示了系統由倍周期分岔通向混沌的道路。
隨后Deane和Hamill研究了電壓型PWM Buck變換器負載并聯電容足夠大情況下的混沌現象[2]。通過解析的方法得到以下迭代式:
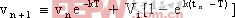 (1)
(1)
其中 可根據方程:
可根據方程: 確定。該方程是超越方程,無法求解。系統是否穩定要根據相圖的梯度確定的。結論是為了使該系統穩定運行,必須保證
確定。該方程是超越方程,無法求解。系統是否穩定要根據相圖的梯度確定的。結論是為了使該系統穩定運行,必須保證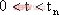 時,
時,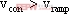 ;
;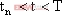 時,
時,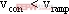 ,其中
,其中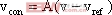 ,
,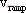 是三角波電壓,v是輸出電壓,
是三角波電壓,v是輸出電壓, 是參考電壓,A是反饋系數。據此條件可以確定系統穩定運行的輸入電壓
是參考電壓,A是反饋系數。據此條件可以確定系統穩定運行的輸入電壓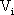 的范圍,若超出參數范圍,系統運行中會出現多脈沖現象。
的范圍,若超出參數范圍,系統運行中會出現多脈沖現象。
以上對一階DC-DC變換器混沌模型的研究,都是在某些假定條件下進行的,因而與實際情況尚有一定差異。
3.1.2 二階系統
當Buck和Boost變換器工作于連續模態,同時電容C不可忽略時,DC-DC變換器數學模型就要用二階狀態方程表示,所以稱之為二階DC-DC變換器系統。此時該數學模型更接近實際的DC-DC變換器,但是系統的分析比一階系統困難,一般無法用解析的方法,只能用數值方法進行分析。Fossas和Oliver給出了電壓型buck變換器周期1和周期2軌道的數學分析,描述了變換器運行中存在的次諧波、分岔和奇怪吸引子,并對其進行了數值分析。其它一些文獻則采用頻閃映射的方法進行研究。頻閃映射是最常用的一種相圖法,除此之外還有同步切換映射、異步切換映射和成對切換映射。使用相圖法可以很直觀的定性說明變換器運行的特性,是Buck和Boost變換器二階系統研究可以采用的方法,但目前尚沒有廣泛的應用,為進一步推廣這些相圖分析方法,以下將分別加以介紹。
(1) 頻閃映射
頻閃映射是通過在每個鋸齒波周期開始時刻對系統軌跡取樣,得到一系列離散的點而獲得的。其主要思想是確定一個初值,以此初值為變量求解下一周期的解,如此不斷反復,最終得到所需精度的解f (n+1)。因此只要求得f (n+1)與f (n)之間的關系式,就能確定DC-DC功率變換器運行的發展狀況,可以采用bisection法或牛頓-拉夫遜法等不同的迭代法獲得f(n+1)。頻閃映射雖然因為直觀和構造方便而得到了廣泛的應用,但在開關周期T的整數倍時刻,變換器可能沒有相位切換,而出現周期跳躍的現象,這時頻閃映射不能正確的加以區別,采用同步切換映射的方法可以解決這個問題。
(2) 同步切換映射
在開關切換周期T整數倍時刻對狀態向量采樣得到同步切換映射。以k表示采樣時刻,則同步切換映射可以寫為如下形式:
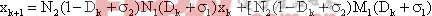
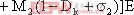 (2)
(2)
其中 和
和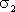 表示
表示 和
和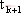 時刻之間相應狀態的跳躍周期的數目。因為在發生周期跳躍現象時不對變量采樣,所以可以解決頻閃映射不能區別跳躍周期的問題。實際上,當
時刻之間相應狀態的跳躍周期的數目。因為在發生周期跳躍現象時不對變量采樣,所以可以解決頻閃映射不能區別跳躍周期的問題。實際上,當 和
和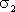 都為零時,同步切換映射就是頻閃映射。
都為零時,同步切換映射就是頻閃映射。
(3) 異步切換映射
連續模態的PWM DC-DC變換器開關狀態的轉換可以用方程: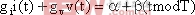 的解來表示,其中
的解來表示,其中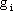 和
和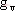 是反饋系數。此方程的解中,不是周期T的整數倍的解定義為異步切換時刻。所謂異步切換映射就是一對異步切換時刻和與之對應的狀態變量,與下一對異步切換瞬間和與之對應的狀態變量之間的關系:
是反饋系數。此方程的解中,不是周期T的整數倍的解定義為異步切換時刻。所謂異步切換映射就是一對異步切換時刻和與之對應的狀態變量,與下一對異步切換瞬間和與之對應的狀態變量之間的關系: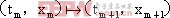 ,m表示第m個異步開關時刻。這種離散映射法也適用于其它所有的基本拓撲。
,m表示第m個異步開關時刻。這種離散映射法也適用于其它所有的基本拓撲。
(4) 成對切換映射
成對切換映射在描述多脈沖行為時有良好的效果。多脈沖就是在一個周期內出現幾次開關切換的現象。不管變換器的工作狀態如何,系統總是從狀態2(或1)切換到狀態1(或2),然后又到狀態2(或1),如此反復。若定義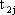 為從狀態1轉換到狀態2的時刻,并以此為初始時刻,則系統保持狀態2到時刻
為從狀態1轉換到狀態2的時刻,并以此為初始時刻,則系統保持狀態2到時刻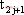 ;在時刻
;在時刻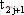 到時刻
到時刻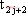 系統保持狀態1。因此可以認為系統狀態是按照“狀態2-狀態1”或是“狀態1-狀態2”的序列進行切換的。設
系統保持狀態1。因此可以認為系統狀態是按照“狀態2-狀態1”或是“狀態1-狀態2”的序列進行切換的。設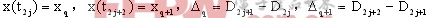 ,可得:
,可得:
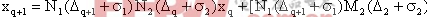

假設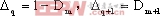 ,則由上式可得到異步切換映射。
,則由上式可得到異步切換映射。
成對切換映射可以認為是分析二階變換系統的最普通的映射,其基本的映射是唯一的。
3.2分析方法
DC-DC變換器混沌現象是一種復雜的非線性運動,具有自身特殊的動態特性,其研究需要借助一些特殊的非線性分析方法,下面介紹幾種最常用也是最有效的方法。
3.2.1功率譜
混沌狀態的特性之一是具有連續的寬帶頻譜,通過功率譜分析可以對混沌進行識別。但這種方法在實驗過程中及自然狀態下具有一定的局限性。因為實際條件下系統中存在的噪聲會與混沌相混淆,所以連續寬帶頻譜只能作為混沌存在的必要條件,而非充分條件。而數值計算研究中因為不會引入外部噪聲,所以可將連續寬帶頻譜作為混沌存在的一個判據。計算機上的快速傅立葉變換Fast Fourier Transform(FFT)和實時頻譜分析儀的普及,使得功率譜分析變得簡單易行。此方法已應用于DC-DC變換器的非線性現象研究,在數值研究及實驗研究兩方面均發揮了重要作用。
3.2.2龐加萊截面和分叉圖截面和分叉圖
基于離散映射可得到反映系統動態過程的龐加萊截面,以及由此衍生的奇怪吸引子[10,12,13]和分叉圖。系統的混沌運動是一個復雜的動態過程,研究其相軌是及其困難的,需要構造龐加萊截面來研究。因為各種動態過程反映在龐加萊截面上的結構具有各自鮮明的特點,如周期運動對應為一個或有限個點,準周期運動對應一個環面,而混沌則對應具有一定結構的、在相空間占據有限范圍的奇怪吸引子,于是就能很容易地區分不同的運動狀態。分叉圖是選擇龐加萊截面的某個狀態變量作為分叉圖的其中一維坐標,另一維則是分叉參數。于是通過分叉圖即可總覽系統隨參數變化而發生的動態特性的變化。
3.2.3 Lyapunov指數
動態系統的相鄰軌道在系統演化過程中可以拉伸和壓縮,其速率可能在相空間中各點不同,只有對運動軌跡各點的拉伸或壓縮速率進行長期平均,才能刻畫動態系統的整體效果,這就是Lyapunov指數的概念。正的Lyapunov指數刻畫了混沌系統的主要特征,它表明:運動軌跡在每個局部都不穩定;相鄰軌道以指數的速率分離;軌道在整體性的穩定因素(有界、耗散)作用下反復折疊,形成混沌吸引子。N維映射有n個拉伸或壓縮方向,各方向分別對應一個Lyapunov指數。
[next]4 DC-DC變換器混沌發展方向及未來應用
4.1 混沌控制
DC-DC變換器混沌控制是一個新的概念和嘗試,借助已發展起來的混沌控制方法如參數擾動法(特別是OGY方法)、納入軌道和強迫遷徙方法、工程反饋控制方法以及智能控制方法等等,可以實現對DC-DC變換器混沌現象的消除、抑制或利用,已引起了非常廣泛的注意和興趣。
DC-DC變換器的混沌控制也取得了一定的成果。Roberto等人將OGY方法用于控制簡單的一階boost電路獲得了成功,C.Batlle等人應用延遲反饋法來控制buck變換器,并得到控制參數的取值范圍的解析條件。此外,Banerjee又提出了兩種完全不同的控制方法:外加參數擾動法和開關切換控制法,對buck和boost變換器的成功控制說明了方法的可行性。DC-DC變換器的反混沌控制研究則尚處于起步階段。
4.2 利用混沌功率譜特性提高電磁兼容性
DC/DC開關變換器最主要的電磁干擾源,來自其較高的工作頻率(一般都達到幾十kHz,最高可以達到幾百kHz)和非線性的開關特性對周圍的電磁環境的影響。此外開關變換器電路設計不當、元件選擇不當以及結構布局或布線不合理都將造成的電磁干擾及使電磁干擾增大。
目前,抑制DC/DC開關變換器電磁干擾的措施,主要是采用附加硬件的技術,如利用金屬或高分子材料屏蔽開關變換器電磁藕合輻射;利用電阻型、電介質型和磁介質型吸波材料將開關變換器所產生的電磁輻射能量轉化為其它能量(主要是熱能)而耗散掉;利用各種濾波器或用高功率因數整流器抑制開關變換器傳導電磁干擾,以及利用接地、浮置、光電耦合、PCB板布線技術減少電磁干擾傳播和發射。這些技術應用的最大缺點是增加開關變換器成本和體積,都沒針對變換器的實際情況有根據開關變換器的特點,從機理上根本抑制開關變換器電磁干擾的產生。國外一些學者也試圖從機理上解決功率開關變換器電磁干擾問題,如采用軟開關技術減少功率開關管的開關電壓、電流應力,改進功率開關變換器的PWM工作方式以減少高頻電壓電流的諧波,但仍然無法回避附加硬件、增加成本和體積的問題。
對電磁干擾特性的研究表明,若能使電磁干擾的能量均布在整個頻譜范圍,就能消弱電磁干擾的峰值,使DC/DC開關變換器電磁干擾得到抑制。非線性系統混沌特性研究表明,它具有連續頻譜的特性,即在相同的電磁傳輸功率條件下,頻譜平均分配在較寬的范圍內,因此,混沌固有均布頻譜的功能,可以利用混沌來提高DC/DC開關變換器的電磁兼容能力。顯然,該種方法的優點在于無須外加設備,節約了成本。目前,雖然對DC/DC開關變換器混沌頻譜特性還沒有更深入的理解,但提供了應用混沌特性解決DC/DC開關變換器EMI的一個的研究思路,是一個值得探索的研究方向。
4.3 利用混沌同步特性進行均流控制
DC-DC變換器的并聯均流一直是提高變換器容量、可靠性及降低成本的關鍵問題,采用混沌同步特性,可以使兩個系統的輸出特性保持一致,因而可以利用來實現DC-DC變換器的并聯均流,其優點是成本低、均流特性好,無需附加其他硬件,只需在控制策略上加以改進。
4.4 利用混沌初值敏感性提高動態特性
混沌因為其對初值的敏感性,具有非混沌系統所沒有的優越性。對混沌的系統,通過對其參數的微小改變就可以使其穩定于混沌吸引子中的某個周期軌道,或者使系統在不同的周期軌道間進行切換,這些周期軌道都是原系統運動方程的解,所以實現控制只需要很小的控制信號,即很小的能量,而無須改變系統的整體結構。但對于非混沌系統,小擾動只能輕微地改變系統的動力學。由于穩定的周期運動可塑性差,缺乏任意選擇狀態的靈活性,因此在設計系統時,讓系統運行于混沌態(即反混沌)對取得易變性是非常有益的。近年來,反混沌控制開始成為一個研究熱點。這方面的成功例子是美國國家航空和宇宙航行局National Aeronautics and Space Administration(NASA)的科學家們利用天體力學問題對擾動的敏感性,只用了少量的剩余肼燃料,在實現其主要任務后把太空船ISEE-31/C送到了距太陽8千萬英里的地方,首次實現了與彗星的碰撞。
因而給DC-DC變換器動態響應的研究提供了一條新的思路。
[next]5 結論
對DC-DC變換器混沌現象研究僅僅是一個開始,還有許多問題尚待解決。但可以預計,隨著對DC-DC變換器混沌現象研究的進一步深入,DC-DC變換器運動本質將被認識的更加深刻,DC-DC變換器的運行特性將在此基礎上進一步提高,由此產生一些全新的DC-DC變換器設計技術和應用技術,使工業界受益。
參考文獻
[1]J. H. B. Deane, D. C. Hamill, “Instability, subharmonics, and chaos in power electronic systems,” IEEE Trans. Power Electron., Vol. 5, No. 3, Jul. 1990, pp. 260-268.
[2] D. C. Hamill, J. H. B. Deane, and D. J. Jefferies, “Modeling of chaotic DC-DC converters by iterated nonlinear mappings,” IEEE Tran. Power Electron., Vol. 7, No. 1, Jan. 1992, pp. 25-36.
[3] M. di Bernardo, and F. Vasca, “Discrete-time maps for the analysis of bifurcations and chaos in DC/DC converters,” IEEE Trans. Circuits and Syst. I, Vol. 47, No. 2, Feb. 2000, pp. 130-142.
[4]C. K. Tse, and W. C. Y. Chan, “Chaos from a current-programmed #262;uk converter,” International Journal of Circuit Theory and Applications, Vol. 23, 1995, pp. 217-225.
[5] M. Alfayyoumi, A. H. Nayfeh, and D. Borojevic, “Modeling and analysis of switching-mode DC-DC regulators,” International Journal of Bifurcation and Chaos, Vol. 10, No. 2, 2000, pp. 373-390.
[6]M. D. Amore, et al., “A neural network approach for identification of EM field source:Analysis of PCB configuration,” in Proc. IEEE International Symposium on Electromagnetic Compatibility, Vol. 2, 1998, pp. 664-669.
[7] G. Antonini, et al., “EMC characterization of SMPS devices: circuit and radiated emissions model”, IEEE Trans, EMC, Vol.38, No.3, Aug. 1996, pp. 300-309.
[63] G. Venkataramanan, C. Chen, “An examination of radiated electromagnetic emission from hard and soft switched power converters”, in Proc. IEEE Industrial Application Conference(IAS’97),Vol. 2, 1997, pp. 1558-1563.
[8] F. Lin, D. Y. Chen, “Reduction of power supply EMI emission by switching frequency modulation”, IEEE Trans. Power Electron., Vol.9, No. 1, Jan. 1994, pp. 132-137.
DC-DC變換器是開關電源的核心技術,實際運行中常常會出現一些奇異或不規則現象,諸如臨界運行的突然崩潰、不明的電磁噪聲、控制系統的間歇振蕩、系統運行的不穩定和系統無法按設計要求工作等等。這些現象由來已久,然而長期以來人們都把它們歸納為系統故障和外界隨機干擾,影響了DC-DC變換器的研究、設計和開發,使得DC-DC變換器性能的提高受到極大的限制。
眾所周知,DC-DC變換器是一個固有開關非線性系統,因此變換器運行必然遵循非線性運行規律。現有的研究表明已被觀察到DC-DC變換器的奇異或不規則現象是一些典型的混沌現象 [1]。顯然當DC-DC變換器工作在混沌狀態時,混沌運動的貌似隨機性將導致系統的運行狀態無法預測,使DC-DC功率變換器的控制性能受到極大的影響,甚至完全不能工作。因而突破現有在線性范圍內或穩定運行區域內研究DC-DC變換器的局限性,從非線性系統混沌理論的高度探索DC-DC變換器的運行規律,對有效地提高DC-DC變換器運行性能,具有重大的理論和實際意義。
通過對各種DC-DC變換器的混沌現象探索和研究,可以達到如下重要的目的:(1)在變換器設計中優化參數設計,避免有害混沌現象的出現,消除奇異或不規則現象,使DC-DC變換器穩定運行;(2)由于混沌運動中存在很多不穩定的周期軌道,可以采用混沌控制技術,控制DC-DC變換器工作在預期的周期軌道上,從而實現周期軌道的快速變換,使DC-DC變換器的工作性能超常規的提高;(3)利用DC-DC變換器的混沌特性實現常規控制難以實現的技術,如利用混沌功率譜特性降低DC-DC變換器中的電磁干擾、利用混沌同步特性實現DC-DC變換器的均流技術、利用混沌運動的初值敏感性提高DC-DC變換器的動態響應特性等。
為此本文將在簡要介紹非線性混沌理論基礎上,歸納DC-DC變換器混沌運動的基本類型,總結現有DC-DC變換器混沌運動的研究方法,綜合DC-DC變換器混沌現象的抑制或控制技術,提出非線性混沌運動在DC-DC變換器應用的研究思路。
2 DC-DC變換器中的混沌現象
長期以來,對客觀事物運動規律的描述,一直采用確定論和概率論兩種體系,確定論的基礎是牛頓力學,用以描述事物的確定性運動;而概率論的基礎是統計學,用以描述事物的隨機運動,代表性的成果是量子力學。確定性運動和隨機運動被認為是涇渭分明、毫無關系的兩種類型的運動,確定性運動可以用確定性方程所描述,隨機運動只能用統計學規律所描述,沒有人懷疑它們之間存在由此及彼的關系。直到上世紀60年代初,美國氣象學家Lorenz在對大氣對流模型作數值計算時,首先發現了耗散系統中的混沌運動,即發現確定性系統可以產生類似隨機的運動,從而使人們有理由認為許多以往被視為隨機的運動可能是由確定性系統所產生,確定性運動與隨機運動可能存在某種必然的聯系,存在由此及彼的關系。因而混沌運動也被視為上一世紀自相對論和量子力學的第三大重大發現,Lorenz也成為第一個針對現實物理系統進行混沌研究的科學家。
混沌運動的發現,使人們開始重新審視以往許多已被定論的研究成果,幾乎涉及各個科學研究領域,都在證實確定性運動與隨機運動的關系,取得了許多重大的研究成果,澄清了許多重大現象的實際產生原因,并應用混沌特性實現了許多常規定律無法取得工作特性。然而令人遺憾的是對電力電子系統混沌現象的研究,直到上個世紀90年代初才開始引起少數學者的關注,但至今還主要停留在對DC-DC變換器混沌運動的研究上。究其原因,一是電力電子系統本身的非線性復雜性,建立其分析模型十分困難;二是電力電子系統自身還處在一個發展時期,由于其強的應用性,許多基本的問題未得到有效的關注,從而未被解決;三是電力電子系統研究思路,大多還局限于拓撲結構的研究上,以及實際應用上,研究思路尚未轉變;四是電力電子系統研究方法上,仍采用傳統的電路分析理論,對其它新科學理論不夠敏感;五是非線性混沌理論自身仍處在一個完善和發展時期。因而使得對電力電子系統混沌運動的研究處于起步階段,也沒有引起人們廣泛的關注和興趣。
盡管如此,對DC-DC變換器混沌運動的研究也以取得重要的成果,其中對DC-DC變換器混沌運動的基本類型已有深入的了解,歸納起來,DC-DC變換器混沌運動有以下基本類型:
1、 倍周期分岔混沌運動
倍周期分岔是DC-DC變換器最常見和基本的一種現象,其特性表現為隨著變換器參數的變化,系統運動規律從周期運動轉變為倍周期運動,然后進入混沌運動。Buck變換器以及電流模式控制下的Boost變換器都會出現倍周期分岔的混沌運動。
2、 Hopf分岔混沌運動
Hopf分岔混沌運動是指DC-DC變換器隨參數變化,由穩定不動點轉換為周期振蕩直至混沌的DC-DC變換器混沌現象。電壓模式控制下的Boost變換器、電流模式控制下的Cuk變換器都可以產生Hopf分岔混沌運動。
3、 準周期分岔混沌運動
準周期分岔混沌運動是指DC-DC變換器隨參數變化,出現以某個頻率為基生成的一系列周期運動的疊加運動,并由此使DC-DC變換器進入混沌狀態的現象。PWM電壓模式控制下的Boost變換器以及DC-DC變換器開環控制在外施正弦擾動激發下、閉環DC-DC變換器在反饋參數的變化下可以產生準周期分岔混沌運動。
4、 邊界碰撞分岔混沌運動
邊界碰撞分岔混沌運動是指DC-DC變換器,從某個周期狀態突然跳躍混沌狀態。Buck變換器以及電流模式控制下的Boost變換器以及積分電流反饋控制的Buck變換器,在一定參數條件下都可以發生邊界碰撞分岔混沌運動。
[next]3 DC-DC變換器混沌現象的研究方法
3.1建模方法
DC-DC變換器有六種基本形式,其中進行混沌現象研究較多的是buck、boost變換器和 變換器。由于以往的發展起來的大信號模型和小信號模型不適合于非線性現象的研究,因而不同階數DC-DC變換器混沌建模就成為它們混沌現象研究最重要的內容。
3.1 .1一階系統
當Buck和Boost變換器的負載是恒壓源;或者當與負載并聯的電容C足夠大時;或者當Buck和Boost變換器處于不連續工作模態時,Buck和Boost變換器的數學模型就可以用一階狀態方程表示。
Hamill和Jeffries首先對DC-DC變換器的混沌現象進行了理論分析。文中的研究對象是電流型PWM Buck變換器,它以恒壓源為負載,電路工作于連續模態。由系統的一階狀態方程推導出續流電感L上的電流迭代式


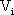
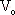
隨后Deane和Hamill研究了電壓型PWM Buck變換器負載并聯電容足夠大情況下的混沌現象[2]。通過解析的方法得到以下迭代式:
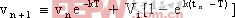
其中


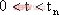
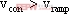
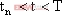
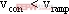
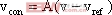
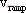

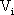
以上對一階DC-DC變換器混沌模型的研究,都是在某些假定條件下進行的,因而與實際情況尚有一定差異。
3.1.2 二階系統
當Buck和Boost變換器工作于連續模態,同時電容C不可忽略時,DC-DC變換器數學模型就要用二階狀態方程表示,所以稱之為二階DC-DC變換器系統。此時該數學模型更接近實際的DC-DC變換器,但是系統的分析比一階系統困難,一般無法用解析的方法,只能用數值方法進行分析。Fossas和Oliver給出了電壓型buck變換器周期1和周期2軌道的數學分析,描述了變換器運行中存在的次諧波、分岔和奇怪吸引子,并對其進行了數值分析。其它一些文獻則采用頻閃映射的方法進行研究。頻閃映射是最常用的一種相圖法,除此之外還有同步切換映射、異步切換映射和成對切換映射。使用相圖法可以很直觀的定性說明變換器運行的特性,是Buck和Boost變換器二階系統研究可以采用的方法,但目前尚沒有廣泛的應用,為進一步推廣這些相圖分析方法,以下將分別加以介紹。
(1) 頻閃映射
頻閃映射是通過在每個鋸齒波周期開始時刻對系統軌跡取樣,得到一系列離散的點而獲得的。其主要思想是確定一個初值,以此初值為變量求解下一周期的解,如此不斷反復,最終得到所需精度的解f (n+1)。因此只要求得f (n+1)與f (n)之間的關系式,就能確定DC-DC功率變換器運行的發展狀況,可以采用bisection法或牛頓-拉夫遜法等不同的迭代法獲得f(n+1)。頻閃映射雖然因為直觀和構造方便而得到了廣泛的應用,但在開關周期T的整數倍時刻,變換器可能沒有相位切換,而出現周期跳躍的現象,這時頻閃映射不能正確的加以區別,采用同步切換映射的方法可以解決這個問題。
(2) 同步切換映射
在開關切換周期T整數倍時刻對狀態向量采樣得到同步切換映射。以k表示采樣時刻,則同步切換映射可以寫為如下形式:
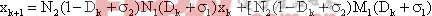
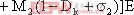
其中

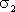

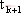

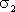
(3) 異步切換映射
連續模態的PWM DC-DC變換器開關狀態的轉換可以用方程:
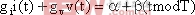
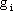
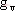
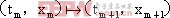
(4) 成對切換映射
成對切換映射在描述多脈沖行為時有良好的效果。多脈沖就是在一個周期內出現幾次開關切換的現象。不管變換器的工作狀態如何,系統總是從狀態2(或1)切換到狀態1(或2),然后又到狀態2(或1),如此反復。若定義
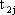
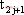
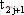
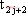
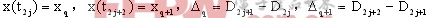
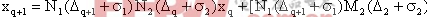

假設
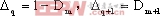
成對切換映射可以認為是分析二階變換系統的最普通的映射,其基本的映射是唯一的。
3.2分析方法
DC-DC變換器混沌現象是一種復雜的非線性運動,具有自身特殊的動態特性,其研究需要借助一些特殊的非線性分析方法,下面介紹幾種最常用也是最有效的方法。
3.2.1功率譜
混沌狀態的特性之一是具有連續的寬帶頻譜,通過功率譜分析可以對混沌進行識別。但這種方法在實驗過程中及自然狀態下具有一定的局限性。因為實際條件下系統中存在的噪聲會與混沌相混淆,所以連續寬帶頻譜只能作為混沌存在的必要條件,而非充分條件。而數值計算研究中因為不會引入外部噪聲,所以可將連續寬帶頻譜作為混沌存在的一個判據。計算機上的快速傅立葉變換Fast Fourier Transform(FFT)和實時頻譜分析儀的普及,使得功率譜分析變得簡單易行。此方法已應用于DC-DC變換器的非線性現象研究,在數值研究及實驗研究兩方面均發揮了重要作用。
3.2.2龐加萊截面和分叉圖截面和分叉圖
基于離散映射可得到反映系統動態過程的龐加萊截面,以及由此衍生的奇怪吸引子[10,12,13]和分叉圖。系統的混沌運動是一個復雜的動態過程,研究其相軌是及其困難的,需要構造龐加萊截面來研究。因為各種動態過程反映在龐加萊截面上的結構具有各自鮮明的特點,如周期運動對應為一個或有限個點,準周期運動對應一個環面,而混沌則對應具有一定結構的、在相空間占據有限范圍的奇怪吸引子,于是就能很容易地區分不同的運動狀態。分叉圖是選擇龐加萊截面的某個狀態變量作為分叉圖的其中一維坐標,另一維則是分叉參數。于是通過分叉圖即可總覽系統隨參數變化而發生的動態特性的變化。
3.2.3 Lyapunov指數
動態系統的相鄰軌道在系統演化過程中可以拉伸和壓縮,其速率可能在相空間中各點不同,只有對運動軌跡各點的拉伸或壓縮速率進行長期平均,才能刻畫動態系統的整體效果,這就是Lyapunov指數的概念。正的Lyapunov指數刻畫了混沌系統的主要特征,它表明:運動軌跡在每個局部都不穩定;相鄰軌道以指數的速率分離;軌道在整體性的穩定因素(有界、耗散)作用下反復折疊,形成混沌吸引子。N維映射有n個拉伸或壓縮方向,各方向分別對應一個Lyapunov指數。
[next]4 DC-DC變換器混沌發展方向及未來應用
4.1 混沌控制
DC-DC變換器混沌控制是一個新的概念和嘗試,借助已發展起來的混沌控制方法如參數擾動法(特別是OGY方法)、納入軌道和強迫遷徙方法、工程反饋控制方法以及智能控制方法等等,可以實現對DC-DC變換器混沌現象的消除、抑制或利用,已引起了非常廣泛的注意和興趣。
DC-DC變換器的混沌控制也取得了一定的成果。Roberto等人將OGY方法用于控制簡單的一階boost電路獲得了成功,C.Batlle等人應用延遲反饋法來控制buck變換器,并得到控制參數的取值范圍的解析條件。此外,Banerjee又提出了兩種完全不同的控制方法:外加參數擾動法和開關切換控制法,對buck和boost變換器的成功控制說明了方法的可行性。DC-DC變換器的反混沌控制研究則尚處于起步階段。
4.2 利用混沌功率譜特性提高電磁兼容性
DC/DC開關變換器最主要的電磁干擾源,來自其較高的工作頻率(一般都達到幾十kHz,最高可以達到幾百kHz)和非線性的開關特性對周圍的電磁環境的影響。此外開關變換器電路設計不當、元件選擇不當以及結構布局或布線不合理都將造成的電磁干擾及使電磁干擾增大。
目前,抑制DC/DC開關變換器電磁干擾的措施,主要是采用附加硬件的技術,如利用金屬或高分子材料屏蔽開關變換器電磁藕合輻射;利用電阻型、電介質型和磁介質型吸波材料將開關變換器所產生的電磁輻射能量轉化為其它能量(主要是熱能)而耗散掉;利用各種濾波器或用高功率因數整流器抑制開關變換器傳導電磁干擾,以及利用接地、浮置、光電耦合、PCB板布線技術減少電磁干擾傳播和發射。這些技術應用的最大缺點是增加開關變換器成本和體積,都沒針對變換器的實際情況有根據開關變換器的特點,從機理上根本抑制開關變換器電磁干擾的產生。國外一些學者也試圖從機理上解決功率開關變換器電磁干擾問題,如采用軟開關技術減少功率開關管的開關電壓、電流應力,改進功率開關變換器的PWM工作方式以減少高頻電壓電流的諧波,但仍然無法回避附加硬件、增加成本和體積的問題。
對電磁干擾特性的研究表明,若能使電磁干擾的能量均布在整個頻譜范圍,就能消弱電磁干擾的峰值,使DC/DC開關變換器電磁干擾得到抑制。非線性系統混沌特性研究表明,它具有連續頻譜的特性,即在相同的電磁傳輸功率條件下,頻譜平均分配在較寬的范圍內,因此,混沌固有均布頻譜的功能,可以利用混沌來提高DC/DC開關變換器的電磁兼容能力。顯然,該種方法的優點在于無須外加設備,節約了成本。目前,雖然對DC/DC開關變換器混沌頻譜特性還沒有更深入的理解,但提供了應用混沌特性解決DC/DC開關變換器EMI的一個的研究思路,是一個值得探索的研究方向。
4.3 利用混沌同步特性進行均流控制
DC-DC變換器的并聯均流一直是提高變換器容量、可靠性及降低成本的關鍵問題,采用混沌同步特性,可以使兩個系統的輸出特性保持一致,因而可以利用來實現DC-DC變換器的并聯均流,其優點是成本低、均流特性好,無需附加其他硬件,只需在控制策略上加以改進。
4.4 利用混沌初值敏感性提高動態特性
混沌因為其對初值的敏感性,具有非混沌系統所沒有的優越性。對混沌的系統,通過對其參數的微小改變就可以使其穩定于混沌吸引子中的某個周期軌道,或者使系統在不同的周期軌道間進行切換,這些周期軌道都是原系統運動方程的解,所以實現控制只需要很小的控制信號,即很小的能量,而無須改變系統的整體結構。但對于非混沌系統,小擾動只能輕微地改變系統的動力學。由于穩定的周期運動可塑性差,缺乏任意選擇狀態的靈活性,因此在設計系統時,讓系統運行于混沌態(即反混沌)對取得易變性是非常有益的。近年來,反混沌控制開始成為一個研究熱點。這方面的成功例子是美國國家航空和宇宙航行局National Aeronautics and Space Administration(NASA)的科學家們利用天體力學問題對擾動的敏感性,只用了少量的剩余肼燃料,在實現其主要任務后把太空船ISEE-31/C送到了距太陽8千萬英里的地方,首次實現了與彗星的碰撞。
因而給DC-DC變換器動態響應的研究提供了一條新的思路。
[next]5 結論
對DC-DC變換器混沌現象研究僅僅是一個開始,還有許多問題尚待解決。但可以預計,隨著對DC-DC變換器混沌現象研究的進一步深入,DC-DC變換器運動本質將被認識的更加深刻,DC-DC變換器的運行特性將在此基礎上進一步提高,由此產生一些全新的DC-DC變換器設計技術和應用技術,使工業界受益。
參考文獻
[1]J. H. B. Deane, D. C. Hamill, “Instability, subharmonics, and chaos in power electronic systems,” IEEE Trans. Power Electron., Vol. 5, No. 3, Jul. 1990, pp. 260-268.
[2] D. C. Hamill, J. H. B. Deane, and D. J. Jefferies, “Modeling of chaotic DC-DC converters by iterated nonlinear mappings,” IEEE Tran. Power Electron., Vol. 7, No. 1, Jan. 1992, pp. 25-36.
[3] M. di Bernardo, and F. Vasca, “Discrete-time maps for the analysis of bifurcations and chaos in DC/DC converters,” IEEE Trans. Circuits and Syst. I, Vol. 47, No. 2, Feb. 2000, pp. 130-142.
[4]C. K. Tse, and W. C. Y. Chan, “Chaos from a current-programmed #262;uk converter,” International Journal of Circuit Theory and Applications, Vol. 23, 1995, pp. 217-225.
[5] M. Alfayyoumi, A. H. Nayfeh, and D. Borojevic, “Modeling and analysis of switching-mode DC-DC regulators,” International Journal of Bifurcation and Chaos, Vol. 10, No. 2, 2000, pp. 373-390.
[6]M. D. Amore, et al., “A neural network approach for identification of EM field source:Analysis of PCB configuration,” in Proc. IEEE International Symposium on Electromagnetic Compatibility, Vol. 2, 1998, pp. 664-669.
[7] G. Antonini, et al., “EMC characterization of SMPS devices: circuit and radiated emissions model”, IEEE Trans, EMC, Vol.38, No.3, Aug. 1996, pp. 300-309.
[63] G. Venkataramanan, C. Chen, “An examination of radiated electromagnetic emission from hard and soft switched power converters”, in Proc. IEEE Industrial Application Conference(IAS’97),Vol. 2, 1997, pp. 1558-1563.
[8] F. Lin, D. Y. Chen, “Reduction of power supply EMI emission by switching frequency modulation”, IEEE Trans. Power Electron., Vol.9, No. 1, Jan. 1994, pp. 132-137.
dc相關文章:dc是什么
pwm相關文章:pwm是什么





評論