閉環反饋控制功率電子變換系統不穩定性抑制技術
4.1 可控阻尼LC輸出濾波器
變換器常規輸出濾波器等效電路如圖4a所示,輸出電壓uO對濾波器前端電壓uAB的傳遞函數為
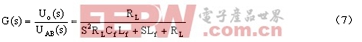
其有效阻尼比
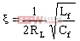
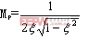
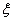
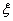
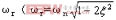
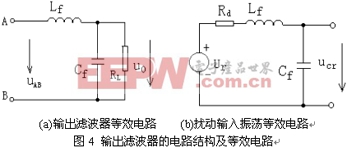
從濾波器瞬態響應角度看,在空載或輕載時,若LC濾波器前端出現一擾動階躍輸入Ur,則濾波器輸出端相應地出現多次振蕩,該振蕩疊加到輸出電壓上,引起輸出電壓誤差較大。為簡化分析,在此僅討論空載時情況,由疊加原理可得其振蕩電路如圖4b所示,Rd包括了引線電阻與感容寄生電阻,其值非常小。由該擾動階躍輸入Ur在濾波器輸出端引起的振蕩電壓分量為
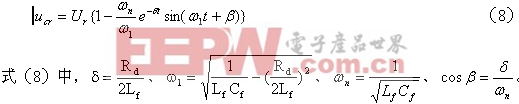
式(8)中第一項就此次擾動而言是個定值,它所引起的電壓誤差量通過反饋控制系統很容易得到調節;因為Rd非常小,故(8)式第二項幅值衰減很慢。雖然控制系統的補償網絡可對其進行一定的調節作用,但由于其頻率ω1和無阻尼自然諧振頻率ωn很接近,若控制系統補償網絡的動態響應速度不是非常迅速時(如電壓單閉環反饋系統),則此時系統的調節作用就比較有限,并且反容易受到該振蕩分量的影響,引起uAB中出現頻率與無阻尼自然諧振頻率ωn相近的諧波分量,LC輸出濾波器不能對其進行有效抑制和濾除,最后表現為輸出電壓基波上疊加有一擾動振蕩諧波分量。
對此,可從兩個方面解決問題。一者可以通過調整控制系統補償網絡或控制策略,提高其動態響應速度來解決。例如讓功率電子變換系統工作在DCM模式、或采用電流控制調制技術,使得輸出濾波器由二階降為一階。這樣對整個系統而言,LC濾波器對穩定性影響減小,從而加大系統穩定性[3]。但電流斷續DCM工作模式只適用于功率較小的場合;電流調制技術較復雜,并且受控制策略的限制。
二者可以在不改變系統整體結構(如控制策略、工作模式等)的情況下加大 ,從而加快(8)式中第二項幅值的衰減,對其進行有效抑制。加大
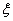
增加Rd有四種方法。一是在圖4b Rd處串接一小電阻Rf(Rd與其相比很小可忽略不計),空載時其傳遞函數為
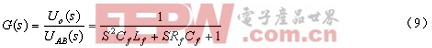
(9)式與(7)式空載時的傳遞函數相比,根軌跡的極點從虛軸向左半平面移動,增加了系統的穩定性;但這種方法在外接負載時流過小電阻Rf的電流很大,會產生過大的損耗。
第二種方法是在濾波電容Cf處并聯一個較大的電阻RLS,經過計算推導,RLS折算成串聯等效

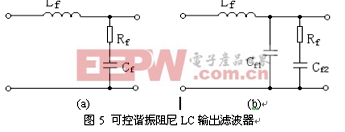
三是在Cf處串接一小電阻Rf,如圖5a所示。這種方法避免了第一種方法在負載時損耗過大的缺點;在空載時第三種方法和第一種方法的電路結構雖然相同,但兩者的傳遞函數并不一樣,第三種方法的傳遞函數為
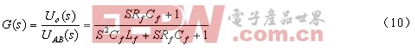
多了一個左半平面的零點,使得根軌跡向左移,增加了系統的穩定性,減小了系統響應的調整時間。但第三種方法會使輸出電壓中高頻諧波濾除得不太干凈,因為小電阻上有小部分高頻諧波壓降,另外在Cf較大時(結合基波頻率時的容抗考慮)小電阻Rf上的損耗也不能忽視。
第四種方法是作者提出的可控諧振阻尼LC輸出濾波器[7],如圖5b所示。為了消除第三種方法的缺點,將Cf一分為二,其中一個電容串一小電阻Rf,Cf=Cf1+Cf2,Cf1會使輸出電壓中的高頻諧波濾除干凈,電阻Rf與Cf2相串可抑制振蕩且使電阻損耗大為減小。Cf2值應盡可能取小以減小電阻Rd上的損耗,一般約為Cf的一半;電阻Rf一般取值幾歐姆~幾十歐姆左右,主要通過和Cf2的容抗比較而定,原則上Rf在遠小于Cf2容抗的前提下盡可能取大但又必須保證其損耗要小,具體可通過計算、計算機仿真和試驗綜合確定。



評論