開關電源的時域數學模型與系統的時域響應

　　對于二階系統，可以采用解析的方法求出其時域響應，而二階系統的分析結論有時也可以應用于高階R 系統的分析。因此，本文將以二階系統或二階電路為例來分析時域特性。最簡單最常用的例子是LO低通濾波器電路，忽略掉電路中的寄生參數后的電路如圖1所示，其中R為LO濾波器電路的負載電阻。

　　系統的時域數學模型，是一組線性或非線性微分方程式或差分方程式。對于圖1所示的二階低通濾波器電路，假設Ui為輸入電壓，輸出為y（t）＝uo（t）則濾波電路的時域數學模型為：

　　圖1 二階低通濾波器電路

　　下面介紹系統的時域響應：

　　圖2所示為二階系統的單位階躍響應y（t）的典型曲線族。由此曲線族可知，在過阻尼時（阻尼比ζ≥1），階躍響應無振蕩、無超調；在欠阻尼時（阻尼比ζ1），單位階躍響應呈阻尼振蕩形式，有一定的超調；在無阻尼時（阻尼比ζ＝0），階躍響應為等幅振蕩，屬于不穩定狀態。

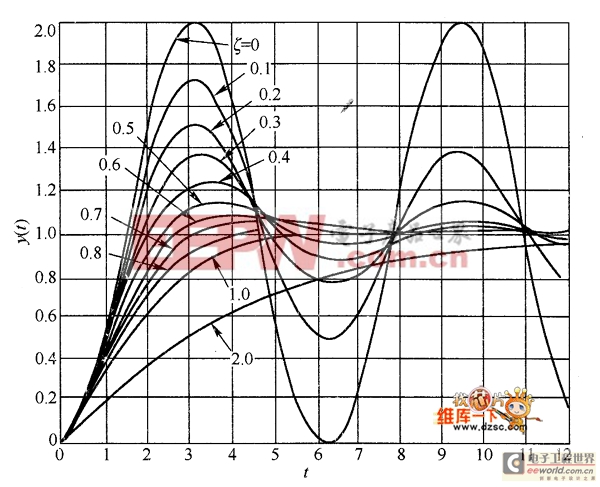
　　圖2 二階系統的單位階躍響應y(t）的典型曲線族

　　對于自動調節系統來說，希望它既能快速響應，又不會過分超調。為此，一般多采用阻尼比ζ來控制，ζ設計在0.4～0.8之間；當ζ0.4，瞬態響應嚴重超調；當ζ＞0.8時，沒有超調，但響應太慢。