數字電源將替代超越模擬電源

本文為您介紹替代傳統模擬控制的數字電源技術：數字電源具有超過模擬方案的巨大優勢，不僅在性能方面(效率、瞬態響應、穩定性等)，而且在上市時間和總擁有成本方面也同樣如此。數字電源正在徹底改變電源的設計方法和實現方式。

基本概況

Intersil用于DC/DC電源轉換的ZL2008第二代自適應數字化電源控制器是一款業界領先的數字電源控制器。它適用于非隔離式降壓、升壓、降壓-升壓和隔離式單管正激或反激式轉換器。在6mm×6mm QFN封裝(圖1)內是一個先進的電源控制器，集成了電源轉換控制、電源管理、故障管理和遙測功能。此外，還包含一個集成的微控制器，可以運行復雜的算法，可以適應超越模擬方案性能的運行。它代表了高性價比的數字電源的最新技術。基本規格見表1。

數字電源架構與模擬架構的對比

圖2顯示了電源轉換控制架構從模擬(a)到現代數字控制(c)的進展。模擬PWM控制器通過使用一個斜坡誤差信號來產生比例占空比。該誤差信號利用電阻和電容網絡進行補償，以修改信號來穩定控制回路。

在數字電源中最早嘗試(圖2b)的比例占空比是通過一個數字計數器(DPWM)生成的，其計數是由數字信號處理器決定的。雖然這種方法在數字實現方面非常強大，但事實證明這種方法過于昂貴，對于大多數實際應用來說需要太多的靜態電流。

在現代數字電源控制(圖2c)當中，占空比仍然是由一個數字計數器生成的，但是現在的計數器是由數字狀態機控制的。這個狀態機是專門為電源控制器(而不是一般功能的DSP)設計的，所以這個解決方案更符合成本效益，且需要較少的靜態電流。

圖2c的架構采用了比例、積分、微分(PID)補償器來穩定電源，而不需要一個完整的DSP來補償電源。誤差電壓的3個要素，誤差的比例、誤差的積分和誤差的微分結合了相對比重，以實現穩定的運行。

請注意，在架構方面數字電源勝過模擬電源具備的一些優勢：數字控制無需外部元件進行補償。這不僅減少了元件數量，而且可以輕而易舉地改變補償，包括隨時改變，甚至隨負載變化進行適應性改變。

典型的情況是沒有數字控制器的外部分壓器。內部參考可以縮放，因此無需使用外部分壓器。這顯然減少了元件數量，而且還有助于在工廠精確校準控制器，這樣用戶就可以受益于高精度，而無需使用昂貴的用于分壓的精密電阻。

數字架構可以簡便地采用數字通信，這樣的操作可以進行配置、控制，且在幾乎沒有外部元件的條件下進行監測。

一種數字電源控制器

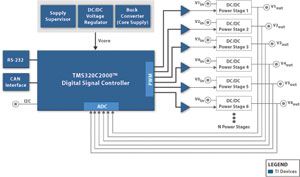
圖3顯示了現代數字電源控制器的基本架構。在該架構中，輸出電壓用一個差分放大器來檢測。這個模擬信號與參考進行比較，生成個誤差信號。該誤差信號被數字化(ADC)，結果通過一個數字補償網絡進行處理，這將在本文稍后的部分中予以描述。數字補償的輸出是一個占空比命令，它設定了數字PWM的持續時間。然后，數字PWM控制就可以FET驅動器，開關電源。

輸出電壓、輸入電壓、輸出電流、溫度都可以使用一個輔助模擬數字轉換器(ADC)進行檢測，ADC可復用到各個檢測點。

配置可以利用引腳跨接、電阻器配置，或通過I2C接口的命令的方式實現。該電源可通過引腳或I2C接口進行控制。配置、操作和環境條件的監測是通過I2C接口實現的。

優勢

1. 更高水平的集成

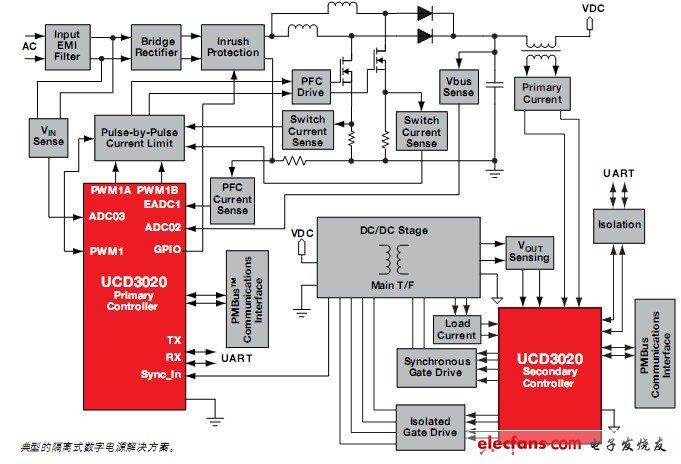
圖4顯示了一個模擬PWM和數字PWM的典型應用原理圖。盡管這兩個控制器共享相同數量的功率傳送(power train)元件(功率FET、電感器、輸入和輸出電容)，模擬控制器仍需要更多的外部元件。這是因為數字控制器集成了許多功能和特性，而這些功能和特性沒有集成在模擬控制器內。如圖所示，數字控制器減少了十幾個元件。在實際實現中，數字控制器已被證明，在中高度復雜設計中可以減少多達60％的外部元件。

2. 穩定性

圖5顯示了一個典型的電源轉換電路。該電源轉換器包括一個帶有固定調制增益Gfix的PWM控制器、高側和低側開關，輸出級包含一個電感器和一個或多個電容，一個負載，以及反饋或控制回路。在這種情況下，反饋控制顯示為Type 3(或III)放大器，但可以是任何反饋控制器。控制回路的用途是將輸出與一個已知參考、VR進行比較，并調整PWM信號來糾正輸出和參考之間的差額。

除了減少元件數量方面的優勢之外，數字化還提供了進一步的優勢，即集成的元件值可表示為存儲在數字寄存器中的值。這有助于根據設計的不同方便地改變這些值，甚至隨時改變，或適應不斷變化的條件。

控制系統做出的任何改變都會對系統引入一種干擾。為實現一個強大而實用的系統，在這種干擾存在的條件下系統必須保持穩定。事實上，它必須在存在一大堆干擾的條件下保持穩定，包括輸入電壓變化、負載變化，甚至溫度變化等等。

我們可以通過反饋路徑增益如何接近-1來描述系統的穩定性。也就是說，在增益接近-1的條件下，反饋有多接近。由于相對于輸出，反饋有一個幅度(增益)和相位，我們可以用增益裕度和相位裕度來表達穩定性，這里的增益裕度是在相位為180度時，測得的相對于單位增益的增益大小有多大，以及在增益為單位增益時，相位裕度是如何接近相對于180度的相位。

相位裕度和增益裕度可以通過奈奎斯特(Nyquist)圖或波特(Bode)圖來確定。由于波特圖有一個容易讀取的頻率范圍，因此是一個方便的工具，這將在本文中使用。

如果沒有反饋，圖5所示系統的簡化傳遞函數可以表示為：

其中：

ωesr是輸出電容esr產生的零點，ωn是輸出級的固有頻率，Q是輸出級的品質因數。

為達到本文的目的，我們將忽略電容esr零點的貢獻，并重點關注傳遞函數的其余極點。也就是說，讓我們來重點關注傳遞函數：

這個方程有兩個極點。對于Q0.5(阻尼情況下)，兩個極點都是實數。對于Q>0.5(欠阻尼情況下)，兩極為復共軛。