垂直侵徹深度計算算法研究

令系統的總擾動項a(t)=f(y，t)+w(t)+(b-b0)u(t)，該擾動項包括內部擾動f(y,t)+(b-b0)u(t)，也包含外部擾動W (t)。把a(t)作為一個擴張的狀態，令x1=y，x2=a(t)，則式(6)的動態系統可寫成如下狀態方程：

式(7)中，令c(t)=a(t)，則可以構造出線性ESO：

式中，-p為觀測器二重極點，p>0。

對應的線性控制律為：

式中，y*為系統的參考輸入。

這是一個二階連續系統，其穩定的充要條件是二重極點P>0。只要選擇合適的期望閉環極點-P>(p>0)，就能保證ESO的觀測效果。

根據永磁同步電機的一階微分方程模型，結合擴張狀態觀測器的設計方法，設計控制器，分析如下：

由式(11)~(12)可看出，負載轉矩、摩擦系數、慣量的擾動以及由于b0估計誤差所造成的擾動都可在a(t)中反映出來。如果能對a(t)進行觀測并予以補償，則可顯著的提高系統的抗擾動能力。控制器結構圖如1所示。

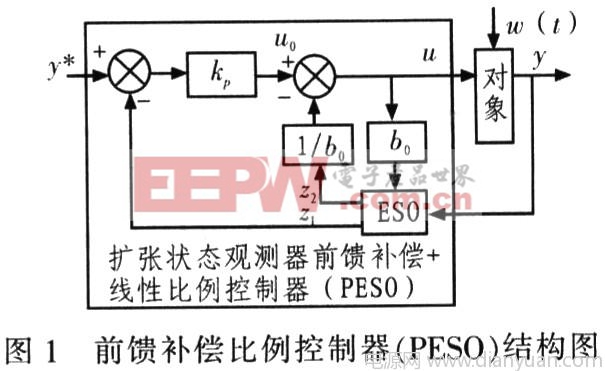
于是得到基于擴張狀態觀測器的比例控制器的表達式：

(1)ESO表達式：

(2)控制律表達式：

根據理論分析，ESO的觀測效果取決于極點-p>(p>0)。和ESO的跟蹤速度有關，P越大，ESO跟蹤輸出信號響應就越快，即z1對速度w的響應就越快。比例增益kp通常應取得較大，但過大會使速度響應振蕩，造成系統不穩定。

4 基于擴張狀態觀測器的控制器算法仿真

在Matlab／Simulink平臺仿真驗證基于擴張狀態觀測器的控制器設計方案。根據圖1搭建控制器的Matlab／Simulink仿真模塊，如圖2所