基于ARM的FIR數字濾波器的軟件實現
(2)誤差函數E(ω)
若定義實值理想頻率響應Hd(ω)在通帶內為1,在阻帶內為0;同時定義加權函數W(ω)在通帶內為δ2/δ1(δ1為通帶波紋,δ1為阻帶波紋),阻帶內為1。則可將加權逼近誤差E(ω)定義為:
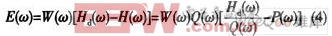
如誤差函數已知,則Chebyshev逼近只需確定濾波器參數{α(k)},然后使其逼近頻帶E(ω)上的最大絕對值最小化。即要找到下式的解:
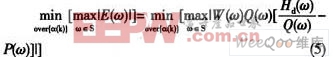
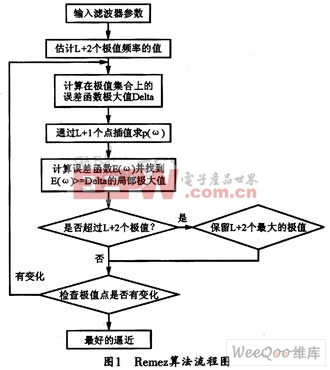
該問題的解法已由Parks和McClellan解決,稱之為Remez交換算法。該算法是建立在交錯定理的基礎上的。圖1所示是Remez算法的流程圖。
(3)交錯定理

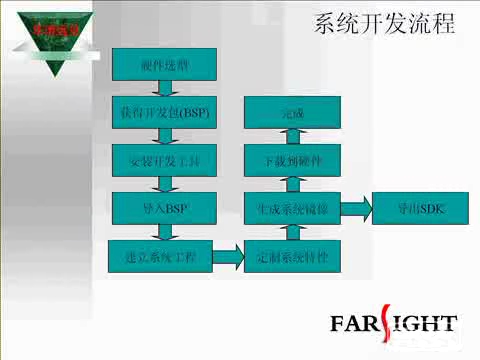
Chebyshev逼近法主要利用Remez交換算法來實現,其設計流程圖如圖1所示。本文主要討論怎樣在ARM平臺上實現該算法,從而設計FIR數字濾波器。其具體設計流程圖如圖2所示,步驟如下:










評論