拉普拉斯變換

在電路分析中，如果將換路時刻作為時間的起點，那么我們只需研究后的電路變量，這樣就可以將函數限定在的區間。這就相當于將函數乘上了單位階躍函數，即：

乘以一個衰減因子，選擇適當的，使得在區間內絕對可積，則它的傅里葉變換為：

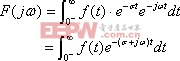（式9-1-1）

（式9-1-1）的積分下限取為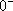，令，則積分結果是S的函數，將（式9-1-1）寫為：

（式9-1-2）

（式9-1-2）中的s稱為復頻率。對于一個時間函數，由（式9-1-2）就可得到一個，通常將稱為原函數，將稱為象函數。

對進行傅里葉反變換，有：

上式兩邊同乘，得：

（式9-1-3）

（式9-1-2）、（式9-1-3）是一對拉普拉斯變換式，（式9-1-2）為拉普拉斯正變換，（式9-1-3）為拉普拉斯反變換，常用手寫體“L”表示拉普拉斯變換，記為：

，

如果時間函數滿足：

（1）時，；

（2）時，和都分段連續，在有限區間內至多存在有限個間斷點；

（3）是指數階函數，即存在常數和，使，從而使積分有限，其中、，則的拉普拉斯變換存在。電路中常見函數一般都是指數階函數。

下面按拉普拉斯變換的定義式（式9-1-2）導出一些常用函數的象函數。

一、指數函數

這里應有。

當時，成為單位階躍函數，于是的拉氏變換為，記為：

當時，可得：

二、單位沖激函數

式中利用了的篩分性質，即：

一些常用函數的拉普拉斯變換式詳見表9-1-1。

表9-1-1 一些常用函數的拉普拉斯變換