一階電路的全響應和三要素法

由外加激勵和非零初始狀態的儲能元件的初始儲能共同引起的響應，稱為全響應，全響應就是微分方程的全解，是方程的特解與其齊次方程的通解之和。

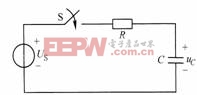
圖8-6-1

如圖8-6-1所示電路，開關S閉合前，電容兩端已有初始電壓，在時刻，開關S閉合，后，列寫電路的KVL方程：

（式8-6-1）

（式8-6-1）與上一節的（式8-5-1）一樣，同理可得：

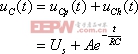（式8-6-2）

根據換路定則：

由（式8-6-2）得：

因此：

最終得到全響應：

（式8-6-3）

現對（式8-6-3）作一個變形，即：

（式8-6-4）

回顧用經典法求解一階電路過渡過程的步驟，發現一階電路的全響應總等于對應的一階線性常系數微分方程的全解，記為，總有：

（式8-6-5）

式中代表方程特解，代表齊次方程的通解，而總為指數形式，則：

（式8-6-6）

取時刻的值：

，

于是得到：

（式8-6-7）

（式8-6-7）就是著名的三要素公式。它是求解一階動態電路的簡便有效的工具。在（式8-6-7）中包含了一階動態電路的三個要素：

：是一階線性常系數微分方程的特解，是一階動態電路在激勵作用下的強制分量。當激勵是直流或正弦交流電源時，強制分量即是穩態分量，這時候，可按直流電路、正弦交流穩態電路的求解方法求得，；

：是響應在換路后瞬間的初始值，按§8-3節中介紹的方法求解：

：是時間常數，一個一階電路只有一個時間常數。或，是電路儲能元件兩端的端口等效電阻。

例8-6-1 如圖8-6-2所示電路，，原來打開，C上無電荷。時閉合，求；當時，又閉合，求。

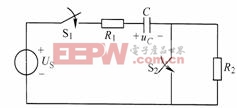
圖8-6-2例8-6-1附圖

解：由題意知：

根據換路定則：

此處激勵為直流，當時，閉合，的穩態值為，即有：

時間常數：

利用三要素公式（式8-6-11）得到：

（V）

當，閉合，有：

在的換路時刻，仍滿足換路定則：

在的換路時刻，仍滿足換路定則：

的穩態值仍為，則：

時間常數：

又因為換路在進行，延遲了，故而根據三要素公式得到：

（V），

例8-6-2 在圖8-6-3所示電路中，，電路已達穩態。時，開關S閉合，求開關S中的過渡電流？

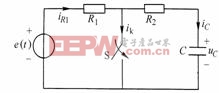
圖8-6-3例8-6-2附圖

解： ，電路已達穩態，可利用相量計算。由KVL得：

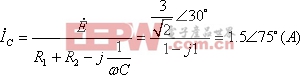
時刻：

根據換路定則：

，且：

畫出時刻的等效電路（圖略），即可求得：

當后，即是穩態開關電流，此時串聯支路被S短接，電容C兩端的電荷已放電完畢，故：

時間常數：

（s）

根據三要素公式：