矩陣形式的節點電壓方程

在第二章中已討論過用節點電壓法（又稱節點電位法）來求解電路。對于不太復雜的電路，可用手工方法來直觀地建立節點電壓方程組，然后求出各節點電位和支路電流。本節介紹用系統方法來建立矩陣形式的節點電壓方程組。在采用計算機輔助分析求解電路問題，如對大規模集成電路的分析計算時，這種方法有較大的優越性。

在討論實際電路問題的時候，首先必須定義一個能代表一般支路結構的典型支路，

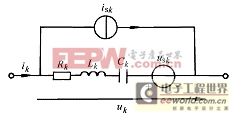
圖 7-6-1

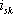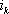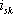圖7-6-1所示為通常采用的不含受控源情況下一種典型支路結構，它由支路元件（電阻、電感及電容），獨立電壓源和獨立電流源所組成，支路電流，支路電壓，及和的參考方向作如圖所示的規定。在實際電路中，如果某條支路不包含獨立電壓源或獨立電流源，則可令對應的或為零。

對于圖7-6-1所示的一般性支路，在正弦穩態情況下，可寫出其支路電壓電流關系式，有：

（7-6-1）

則對于包含有b條支路的網絡，可寫出各支路電壓電流關系式為：

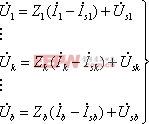（7-6-2）

把上式寫為矩陣形式，有：

（7-6-3）

式中，為支路電壓列向量矩陣；為支路電流列向量矩陣；與為支路中獨立電流源與獨立電壓源列向量矩陣。Z為支路阻抗矩陣，當電路不包含受控源時，它為一對角矩陣，即有：

（7-6-4）

對式（7-6-3）兩邊左乘支路阻抗矩陣的逆矩陣，并解出支路電流列向量為：

（7-6-5）

式中，稱為支路導納矩陣。當Z為對角陣時，Y也為一對角陣，且有：

（7-6-6）

或： （7-6-7）

對式（7-6-5）兩邊左乘關聯矩陣A，考慮到矩陣形式的基爾霍夫電流定律，有：

即有：

由支路電壓與節點電位之間的關系式，上式可寫為：

（7-6-8）

或：

（7-6-9）

式中，稱為節點導納矩陣。上二式即為矩陣形式的節點電壓方程，為待求的節點電位列向量矩陣，式中其余各矩陣元素均可根據求解網絡的實際電路結構和參數，對照典型支路所規定的參考方向分別系統地列寫出來。解式（7-6-9）矩陣方程，可解得節點電位值，進而求出支路電壓值，再由式（7-6-5）求出支路電流值。一般在用矩陣形式的節點電壓方程解題時，包含以下幾個主要步驟：

（1）作有向圖，標出各支路電壓電流參考方向；

（2）對各支路，節點編號；

（3）選定參考節點，建立關聯矩陣A；

（4）參照一般性支路（典型支路）的結構和方向，分別寫出支路導納矩陣Y，支路電壓源列矩陣及支路電流源列矩陣；

（5）根據式（7-6-9）解出節點電位列向量；

（6）由求出支路電壓，由式（7-6-5）求出支路電流，并求出支路中流過元件（阻抗Z）的電流。

例7-6-1 電路如圖7-6-2a所示，各支路阻抗值，電壓源及電流源均如圖。試建立矩陣形式的節點電壓方程式。

解： 電路的有向圖及參考方向見圖7-6-2b。選節點④為參考節點，則可寫出其關聯矩陣A為：

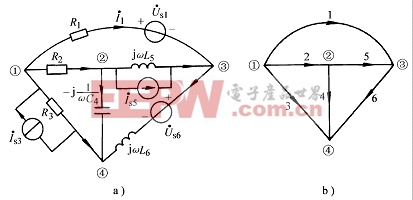
圖 7-6-2

電壓源向量

電流源向量

支路導納矩陣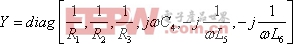

然后寫出其節點導納矩陣為：

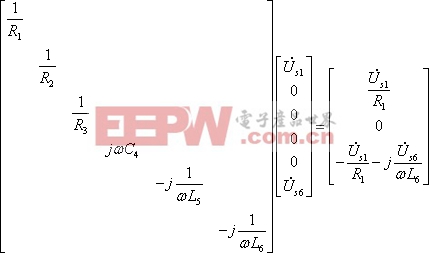
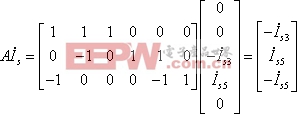
最后可得矩陣形式的節點電壓方程式為：

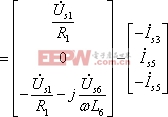
由上可看出，用系統方法建立的節點電壓方程式與第二章中用觀察法直接列寫的結果是完全相同的。雖然在簡單電路的解題中并未體現其特點，但對于大型網絡，可由計算機自動生成方程組。上面的過程可由計算機完成。

上面討論的例子中未包含受控源的情況，如果考慮受控源情況，則矩陣方程的形式要復雜得多。由于受控源有四種形式，且在電路中控制變量可能是支路電壓電流，也可以是元件電壓電流（見上面討論的典型支路），因此想寫出一個包含所有情況的一般性方程形式就會變得很復雜。下面僅分別討論包含元件電流控制的電壓源與元件電壓控制的電流源二種情況。

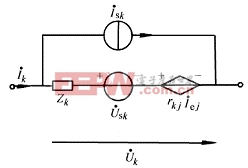
圖 7-6-3

在一般支路中，若包含有元件電流控制的電壓源，則一般支路形式如圖7-6-3所示。圖中為第j條支路中流過元件的電流，, 為控制系數。若設一個有b條支路的電網絡，其中第k支路中有一個受j 支路元件電流控制的電壓源，其方向如圖7-6-3所示，則k支路電壓方程為：

（7-6-10）

而其余支路電壓方程完全與式7-6-2相同。寫出該電路的各支路電壓方程式組，并用矩陣形式表示為：

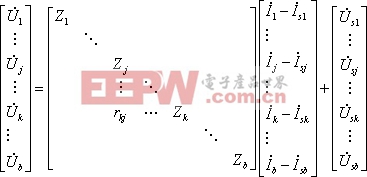（7-6-11）

或記為：

（7-6-12）

上式與不包含受控源時的形式完全相同，其差別在于支路阻抗矩陣Z。對于包含有元件電流控制的電壓源情況，其支路阻抗矩陣Z中第k行（受控電壓源支路號）第j列（控制電流支路號）位置出現一個受控源控制系數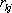。此時支路阻抗矩陣Z不再為對角陣，但其矩陣方程表達式卻與不含受控源完全相同，因此其求解過程也與上面介紹的完全一致。由此可見，對于包含元件電流控制電壓源情況，在列寫矩陣形式節點電壓方程時，只需把受控源控制系數寫入支路阻抗矩陣的對應位置，其余步驟與不含受控源完全相同。

例7-6-2 電路如圖7-6-4所示，各元件參數及電源情況標于圖上，支路1與2之間存在互感，設，試建立矩陣形式的節點電壓方程。

解：互感現象可看成是某一支路控制電流在另一支路中產生的受控電壓源，其控制系數即為互感值。畫出電路的有向圖如圖7-6-4b所示，節點及支路編號如圖，選節點④為參考節點，可寫出其關聯矩陣為：

把互感電壓作為元件電流控制電壓源，控制系數為，參照典型支路圖7-6-3，可寫出支路阻抗矩陣為：

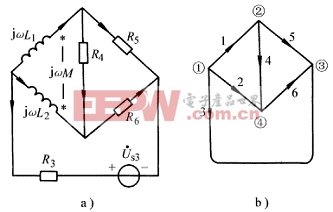
圖 7-6-4

支路導納矩陣為：

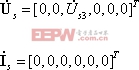
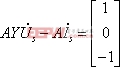
最后可得矩陣方程為：

如果網絡中包含有元件電壓控制的電流源，其一般支路形式如圖7-6-5所示。對于這種形式的電路，可直接列寫出支路電流表達式為：

（7-6-13）

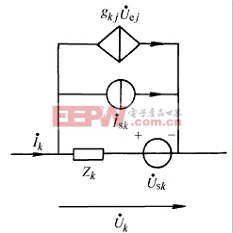
圖 7-6-5

式中，表示由j支路中元件電壓控制k支路中電流源的受控源控制系數。與上面分析受控源情況相同，若b條支路中k支路有一受支路j元件電壓控制的電流源，則可寫出各支路電流方程式，并用矩陣形式表示為：

（7-6-14）

或寫成：

（7-6-15）

可見對于元件電壓控制的電流源情況，可直接列寫支路導納矩陣，把相應的受控源控制系數寫入到Y的對應位置。其余的計算方法與不包含受控源情況完全相同。