關聯矩陣、回路矩陣和割集矩陣的關系

對于同一個電路，若各支路，節點的編號及方向均相同時，其列寫出的關聯矩陣，回路矩陣和割集矩陣之間存在著一定的聯系。

對于圖7-5-1所示的有向圖，選支路1、2、3為樹支，作單樹支割集如圖所示，則可寫出其基本回路矩陣與基本割集矩陣如下：

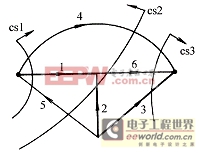
圖 7-5-1

用左乘，可得：

即有：

（7-5-1）

由矩陣性質可得另一形式為：

（7-5-2）

此二式反映了相同編號的網絡中，基本割集矩陣與基本回路矩陣之間的關系。

對于式7-5-1的一般證明可簡略描述如下：令，則D中任一元素為，下標j表示第j條單連支回路，k表示第k個割集，而則表示把第j回路中i支路元素與第k割集中i支路元素相乘。顯然，若i支路不是同時包含在j回路與k割集中，則其乘積必為零。而同時包含在j回路與k割集中的支路條數必為偶數。因為若移去k割集的所有支路，則電路分為獨立的兩部分。若閉合回路跨越兩部分電路，顯然其連接兩部分的支路條數（包含在k割集中）必為偶數條。例如對于圖7-5-1所示的網絡，同時包含在割集1與回路1（由支路4組成的單連支回路）中的支路為4與1。

對于成對出現在回路和割集中的支路，如果二條支路方向與回路一致，（此時對應行中二個元素同號），則該二條支路與割集方向必一正一反（此時對應行中二個元素異號），則的值必為零。反之，若二條支路方向與回路方向一正一反，則相對于割集方向必同號，其乘積亦為零。可見矩陣D中元素均為零，從而可推出式（7-5-1）。

若網絡支路編號嚴格按先樹支后連支編排，則式（7-5-1）可寫為：

即有：

（7-5-3）

式中，表示由樹支組成的回路矩陣子矩陣；表示由連支組成的割集矩陣子矩陣。

對于圖7-5-1的電路，若設節點4為參考節點，寫出它的關聯矩陣為：

用A左乘，得：

即有：

（7-5-4） 或 （7-5-5）

實際上若選擇割集只包圍一個節點，且割集方向離開節點，則這樣組成的割集即為關聯矩陣A，即是說關聯矩陣無非是割集矩陣的一種形式。由式（7-5-1）即可知式（7-5-4）成立。

如果支路編號按先樹支后連支方式，則關聯矩陣可表示為，其中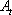表示由所有樹支元素組成的子矩陣，表示由連支元素組成的子矩陣。式（7-5-4）可描述為：

上式左乘，可得：

即有：

（7-5-6）

據此，基本回路矩陣可寫成：

（7-5-7）

從該表達式可見，對于一個支路編號采用先樹支后連支方式的電路，其基本回路矩陣可通過關聯矩陣求得。

同理，由式（7-5-3）及式（7-5-6）可得，，因此基本割集矩陣又可表達為： （7-5-8）

由式可知，基本割集矩陣可由關聯矩陣求得。

當采用計算機輔助計算建立狀態方程時，直接寫回路矩陣或割集矩陣往往比較困難，而推求關聯矩陣卻很方便。因此在實際應用時往往由關聯矩陣通過式（7-5-7）和式（7-5-8）求得回路矩陣與割集矩陣。