正弦交流電路的阻抗、導納及等效轉換

前面幾節已導出電阻、電感和電容元件上電壓與電流的相量關系，引入了電抗和容抗的概念。當電路中激勵源為單一頻率的正弦交流電時，各支路響應電壓電流也為同頻率的正弦量。所以在正弦穩態電路中，任何一個線性的無源二端網絡都可以用一個復數阻抗和導納來表示。

下面考慮RLC串聯電路的情況。設在RLC串聯電路的兩端加角頻率為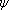的正弦電壓激勵，如圖3-8-1a所示，由前述分析可知，在串聯電路中可產生與激

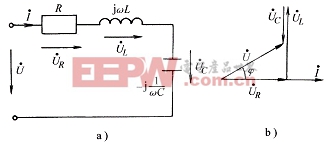
圖 3-8-1

勵電壓同頻率的正弦交流電流i。根據基爾霍夫電壓定律，可得到相量形式的電壓方程

（3-8-1）

令串聯電路中電流表達式為，相量形式為，根據前幾節所述，電壓方程可表示為

（3-8-2）

式中，為該串聯電路的等效復阻抗，它等于端電壓相量與電流相量的比值。阻抗Z的實部為電路的電阻值，虛部為電路的電抗。電抗等于感抗與容抗的差值，它是一個帶符號的代數量。復數阻抗可表示成極坐標的形式

（3-8-3）

式中，z為阻抗的模，；為阻抗角，。

對于任意復雜的無源一端口網絡，當在端口外加一個正弦電壓（或電流）激勵時，網絡中各支路的電流（或電壓）均為與激勵源同頻率的正弦函數。類似于線性電阻一端口網絡可用一個等效電阻來表示一樣，對于任何一個線性無源一端口網絡，也可以用一個等效的入端阻抗或導納來表示。一端口網絡的阻抗Z定義為入端電壓相量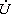與入端電流相量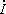之比，即有：

式中取電壓與電流為關聯參考方向。入端導納Y定義為入端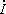電壓與入端電壓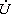之比，即：

式中電壓與電流也取關聯參考方向。

在實際電路計算中，阻抗和導納之間的互相轉換需根據電路串并聯情況而定，下面舉例加以說明。

例3-8-1 圖3-8-3所示電路中，已知，，，試求該電路的入端阻抗。若外加電壓，求各支路電流。

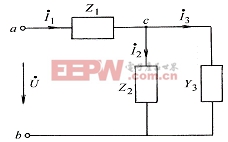
圖 3-8-3

解：先求cb端右面等效阻抗，阻抗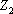的等效導納

則：

cb右端等效阻抗：

電路入端阻抗：

設，則：