基爾霍夫定律的相量形式
前面幾節討論了電阻、電容和電感中電壓電流的時域關系式,以及相應的相量表達式。對于簡單電路,我們已知電路中電壓和電流均為與所施加的激勵源同頻率的正弦量。此結論可推廣到線性穩態的復雜正弦交流電路中去。對于復雜的線性電路,如果所有激勵源均為同一頻率的正弦函數,則各支路的電流和電壓都為和激勵源有相同頻率的正弦函數,都可以表示為相量形式,在電路計算中可采用相量計算的方法。
基爾霍夫節點電流定律的時域表達式為
![]() (3-7-1)
(3-7-1)
因為所有電流均為相同頻率的正弦函數,根據本章第三節內容推導,可把時域求和的表達式轉化為相量求和形式
![]() (3-7-2)
(3-7-2)
此式表明,對于任一節點,流出節點的電流相量之和等于零。此即為相量形式的基爾霍夫節點電流定律。
基爾霍夫電壓定律指出,電路中任一閉合回路的各支路電壓降之和為零,即
![]() (3-7-3)
(3-7-3)
可得相量形式的基爾霍夫電壓定律
![]() (3-7-4)
(3-7-4)
把節點電流或回路電壓的相量作成相量圖,可得到一個閉合的相量多邊形。在計算分析正弦交流電路中,可利用上述兩個定律及相量關系。下面舉幾個例子加以說明。
例3-7-1 圖3-7-1a的電路中,已知![]() ,
,![]() ,求
,求![]() 的值。
的值。
解:由基爾霍夫電壓定律,![]() 得:
得:
![]() ,圖3-7-1b中畫出了電壓的相量圖。
,圖3-7-1b中畫出了電壓的相量圖。
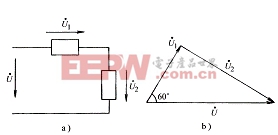
圖 3-7-1










評論