4.6.1 參數根軌跡 ⒈引言 前面討論系統根軌跡的繪制方法時,都是以開環增益K為可變參數,這是在實際上最常見的情況。上述以開環增益K 為可變參量繪制的根軌跡稱為常規根軌跡。從理論上講,可變參量可以選擇為系統的任何參數,如開環零、極點,時間常數和反饋系數等,這種以K以外的系統其他參量作為可變參量繪制的根軌跡,稱作參數根軌跡,又稱廣義根軌跡。用參數根軌跡可以分析系統中的各種參數,如開環零、極點,時間常數和反饋系數等對于系統性能的影響。
⒉思路和方法
如果選擇系統其他參量為可變參量時,引入等效傳遞函數的概念,即作一個變換,使得此可變參量在等效傳遞函數中相當于開環增益K的位置,則上面介紹的幅角、幅值條件和繪制根軌跡的各種規則都依然有效。
上述變換的方法是對系統的特征方程作一個除法,即以特征方程中不含有該參數項的各項去除該方程,便可得到 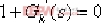 的形式,其中 的形式,其中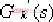 ,就是要引入的等效傳遞函數。 ,就是要引入的等效傳遞函數。
例4-4 設反饋系統如圖4-16所示 ,試繪制以a為參變量的根軌跡。 ⑴. 常規方法 ⑴. 系統的開環傳遞函數為 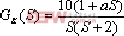 系統的特征方程為 
以不含a的項,即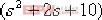 ,除以上式得 ,除以上式得 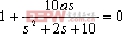
得等效開環傳遞函數: 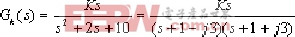
式中 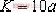 據此,可用“常規方法”作出其根跡,如圖4-17所示(可證明,其部分根跡為園弧)。 ①.根跡的起迄點及條數:
兩條根跡分支,分別起始于開環極點-1+j3、-1-j3,終止于開環零點0和s平面∞處。 ②.實軸上的根跡:
負半實軸為根跡。 ③.會合點: 由 。 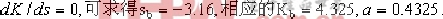
④.復數極點-1+j3出射角:
⑵.“MATLAB”方法 ①解本題的MATLAB程序exe44.m % ks/(s2+2s+10)
n=[1 0]
d=[1 2 10]
rlocus(n,d) ②執行本程序,可得圖4-17參數根軌跡圖。
4.6.2 多回路系統的根軌跡
1.引言 前面介紹單環系統根跡,不僅適合單環,而且也適合多環系統。
2.思路和方法
先作內環根跡,再用幅值條件試探求出內環的閉環極點,進而作為外環的一部分開環極點,再畫出外環的根跡。 例4-5 設一雙環反饋系統,如圖4-18所示 。試繪制以 c為參變量的根軌跡。 ⑴.常規方法 ①.先作內環根跡:
內環開環傳遞函數為: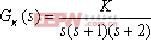 此與例4-1相同,這里不再重復。 ②.求出 =1.06 時的內環閉環極點(用試探法):
由§4―3可知,為:-0.33+j0.58、 -0.33-j0.58、 -2.33 ③.內環的閉環傳遞函數為: 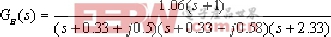
④. 內環化簡后外環的開環的傳遞函數為:
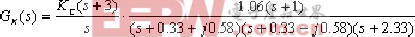
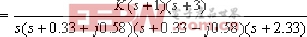
⑤.外環(系統)根軌跡: ·根軌跡有四條分支: 分別自0, -2.33,-033+j0.58,0.33-j0.58。至-1,-3,和s平面∞處。 ·實軸上根跡: 在 0 至-1,-2至-2.33,-3至-∞是根軌跡。 ·根跡漸近線: 由公式求得σα=0.5,α=±90B 。 ·復數極點-0.33+j0.58,外的出射角: φ=8.06B 。 ·根跡與虛軸交點: 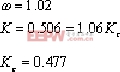
·系統外環根跡: 如圖4-19所示. ⑵.“MATLAB”方法 ①.解本題的MATLAB程序exe45.m:
% k(s+1)(s+3)/s(s+0.33+0.58i)(s+0.33-0.58i)(s+2.33)
z=[-1 –3]’;
p=[0 –2.33 –0.33+0.58i –0.33-0.58i]’;
k=1;
[n,d]=zp2tf(z,p,k);
rlocus(n,d)
title(‘4-19’) ②.執行本程序,可得外環根軌跡圖4-19。 |
評論