基于譜分析的渦街流量信號處理
在仿真分析非整周期采樣對譜分析法影響的基礎上,對基于譜分析的實際渦街流量信號處理方法進行了有益地探討。
關鍵詞:非整周期采樣;頻譜分析;渦街流量信號處理
Vortex Signal Processing Based on Spectrum Analysis
LIN Min
(Medical Instrumentation College, Shanghai Science Technology University,
Shanghai 200093, China)
Shanghai 200093, China)
Key words: sampling in non?complete periods; spectrum analysis; vortex signal processing
1引言
渦街流量信號處理的核心問題是擴展渦街流量計在低頻段的量程下限。而嘗試運用譜分析方法解決這一問題是目前的研究熱點之一。文獻[1]~[3]采用仿真方法比較了基于FFT的周期圖譜法和基于BURG的最大熵譜法,并得出結論:FFT算法所需采樣數據多,適合抑制低頻確定性噪聲;而BURG算法所需數據少,適合抑制隨機噪聲。但是他們是用信號發生器產生的理想波形來進行譜分析研究的,沒有計算實際渦街信號的頻譜。另外,該頻譜分析是在對信號進行整周期采樣的基礎上實現的,而實際系統由于未知信號頻率,不可能對渦街輸出信號實現整周期采樣,因而整周期采樣只是理想情況,在實際系統中幾乎不可能實現。
鑒于此,本文在將譜分析運用到實際的流量信號處理前,有必要先通過Matlab軟件來仿真分析非整周期采樣對譜分析處理結果的影響,以減少研制中的盲目性和縮短研究周期。
渦街流量信號處理的核心問題是擴展渦街流量計在低頻段的量程下限。而嘗試運用譜分析方法解決這一問題是目前的研究熱點之一。文獻[1]~[3]采用仿真方法比較了基于FFT的周期圖譜法和基于BURG的最大熵譜法,并得出結論:FFT算法所需采樣數據多,適合抑制低頻確定性噪聲;而BURG算法所需數據少,適合抑制隨機噪聲。但是他們是用信號發生器產生的理想波形來進行譜分析研究的,沒有計算實際渦街信號的頻譜。另外,該頻譜分析是在對信號進行整周期采樣的基礎上實現的,而實際系統由于未知信號頻率,不可能對渦街輸出信號實現整周期采樣,因而整周期采樣只是理想情況,在實際系統中幾乎不可能實現。
鑒于此,本文在將譜分析運用到實際的流量信號處理前,有必要先通過Matlab軟件來仿真分析非整周期采樣對譜分析處理結果的影響,以減少研制中的盲目性和縮短研究周期。
假設流量計的輸出信號為
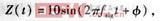 ?
?
信號頻率fsig=20Hz。從t=0時刻開始采樣,總采樣時間保持不變。則當φ=360°·k,k=0、1、2、…時為整周期采樣。為了比較非整周期采樣對FFT譜分析和BURG熵譜分析的影響,我們分別取N=1024點、在64個整周期的基礎上進行FFT計算以及取N=128點、在16個整周期的基礎上進行BURG計算,并令偏移角φ=0°,5°,10°,…,180°,即以5°步長遞增來仿真計算非整周期采樣對兩種算法的功率譜峰值P和頻率估計值f的影響。現將兩組計算結果分別繪成圖1和圖2,以供更直觀地分析。圖中,橫坐標代表信號頻率值f(Hz);縱坐標代表放大1000倍的功率譜密度值P(W/Hz)。
信號頻率fsig=20Hz。從t=0時刻開始采樣,總采樣時間保持不變。則當φ=360°·k,k=0、1、2、…時為整周期采樣。為了比較非整周期采樣對FFT譜分析和BURG熵譜分析的影響,我們分別取N=1024點、在64個整周期的基礎上進行FFT計算以及取N=128點、在16個整周期的基礎上進行BURG計算,并令偏移角φ=0°,5°,10°,…,180°,即以5°步長遞增來仿真計算非整周期采樣對兩種算法的功率譜峰值P和頻率估計值f的影響。現將兩組計算結果分別繪成圖1和圖2,以供更直觀地分析。圖中,橫坐標代表信號頻率值f(Hz);縱坐標代表放大1000倍的功率譜密度值P(W/Hz)。
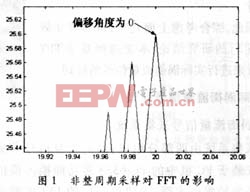

Ⅰ.FFT譜分析在偏角為0°,即整周期采樣時譜峰值P最大,對應的頻率值f也最精確,為20Hz;隨著偏角的增大,譜峰值和頻率均減小。而BURG譜分析在偏角為0°時譜峰值P并非最大,但對應的頻率值f卻最精確,也為20Hz;其譜峰值P與偏角之間無明顯的規律關系。
Ⅱ.FFT譜分析隨著偏角的增大,其各偏角所對應的頻率值近似于線性地遞減,即偏角差值相等,所對應的頻率差值也近似相等。而BURG譜分析不存在這種規律。
Ⅲ.采樣周期數越多,非整周期采樣對這兩種譜分析的影響越小。例如,FFT譜分析在采樣64個周期時的頻率誤差是采樣32個周期時的1/2,是采樣16個周期時的1/4,是采樣8個周期時的1/8。即檢測到的頻率誤差隨采樣周期數線性減少而近似線性增大,FFT譜分析在64、32、16、8個整周期采樣的基礎上偏180°時得到的誤差分別為0.77%、1.54%、3.03%、5.88%。
Ⅳ.FFT譜分析得到的功率譜峰值P準確;譜峰值對應的頻率值準確。而BURG譜分析得到的功率譜峰值P不準確,前后無規律性;但譜峰值所對應的頻率值也準確。
Ⅴ.信號頻率值f與采樣周期數有關。只要周期數取得足夠大時,非整周期采樣帶來的測量誤差就變得很小,可以忽略不計。
因此,綜合考慮上面幾點,再參考文獻[1]~[3]的研究結論,本文選擇基于FFT譜分析來進行實際渦街流量信號的處理。?
Ⅱ.FFT譜分析隨著偏角的增大,其各偏角所對應的頻率值近似于線性地遞減,即偏角差值相等,所對應的頻率差值也近似相等。而BURG譜分析不存在這種規律。
Ⅲ.采樣周期數越多,非整周期采樣對這兩種譜分析的影響越小。例如,FFT譜分析在采樣64個周期時的頻率誤差是采樣32個周期時的1/2,是采樣16個周期時的1/4,是采樣8個周期時的1/8。即檢測到的頻率誤差隨采樣周期數線性減少而近似線性增大,FFT譜分析在64、32、16、8個整周期采樣的基礎上偏180°時得到的誤差分別為0.77%、1.54%、3.03%、5.88%。
Ⅳ.FFT譜分析得到的功率譜峰值P準確;譜峰值對應的頻率值準確。而BURG譜分析得到的功率譜峰值P不準確,前后無規律性;但譜峰值所對應的頻率值也準確。
Ⅴ.信號頻率值f與采樣周期數有關。只要周期數取得足夠大時,非整周期采樣帶來的測量誤差就變得很小,可以忽略不計。
因此,綜合考慮上面幾點,再參考文獻[1]~[3]的研究結論,本文選擇基于FFT譜分析來進行實際渦街流量信號的處理。?
3.1渦街流量信號采集系統
采集系統由兩部分組成:渦街流量信號采集裝置和可安裝于PC機中的PC-6333多功能模入模出接口卡。采集裝置由水管、天津儀表廠的LUGB型渦街流量計、ADMACSE電磁流量計、滬東電機公司的Y90S-2三相異步電動機及水泵、西門子公司的MICROMASTER420變頻器、水箱等部分組成(圖3)。圖中,箭頭的方向表示水流的流向。
采集裝置的工作流程為:啟動變頻器,設置變頻器的顯示頻率,電動機在變頻器的控制下按一定的速度旋轉,帶動水泵工作,將水從水箱抽上來。水流經過電磁流量計,顯示瞬時的流量百分比,再經渦街流量計檢測后返回到水箱。渦街流量計的輸出模擬信號由PC-6333模入模出接口卡轉換成數字信號后送入PC機中再作進一步處理。
3.2基于譜分析的渦街流量信號處理與分析
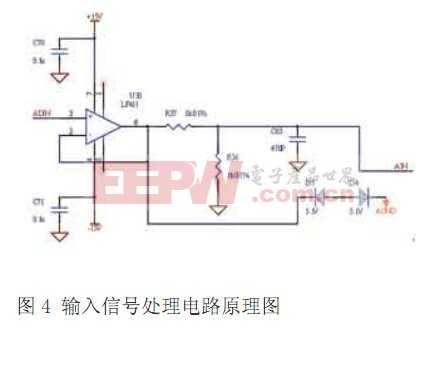
通過變頻器設置水泵工作頻率為50Hz、47.5Hz、45Hz、……,以2.5Hz的步長逐漸降低,當低于35Hz時,水泵電動機就自動逐漸地停止旋轉。對應每一個頻率點,分別采樣2048點數據。將2048點采樣數據載入Matlab程序中,通過sptool工具箱對其進行近似整周期FFT計算。為了便于比較和提高計算精度,在每個泵頻率點上,我們取了兩段不同范圍的采樣數據,每一段都近似整周期采樣,再求取兩段的FFT平均值,如圖4所示。橫坐標表示譜分析得到的頻率平均值f(Hz);縱坐標表示各泵頻率點上電磁流量計顯示的流量平均值(%)。
采集系統由兩部分組成:渦街流量信號采集裝置和可安裝于PC機中的PC-6333多功能模入模出接口卡。采集裝置由水管、天津儀表廠的LUGB型渦街流量計、ADMACSE電磁流量計、滬東電機公司的Y90S-2三相異步電動機及水泵、西門子公司的MICROMASTER420變頻器、水箱等部分組成(圖3)。圖中,箭頭的方向表示水流的流向。
采集裝置的工作流程為:啟動變頻器,設置變頻器的顯示頻率,電動機在變頻器的控制下按一定的速度旋轉,帶動水泵工作,將水從水箱抽上來。水流經過電磁流量計,顯示瞬時的流量百分比,再經渦街流量計檢測后返回到水箱。渦街流量計的輸出模擬信號由PC-6333模入模出接口卡轉換成數字信號后送入PC機中再作進一步處理。
3.2基于譜分析的渦街流量信號處理與分析
通過變頻器設置水泵工作頻率為50Hz、47.5Hz、45Hz、……,以2.5Hz的步長逐漸降低,當低于35Hz時,水泵電動機就自動逐漸地停止旋轉。對應每一個頻率點,分別采樣2048點數據。將2048點采樣數據載入Matlab程序中,通過sptool工具箱對其進行近似整周期FFT計算。為了便于比較和提高計算精度,在每個泵頻率點上,我們取了兩段不同范圍的采樣數據,每一段都近似整周期采樣,再求取兩段的FFT平均值,如圖4所示。橫坐標表示譜分析得到的頻率平均值f(Hz);縱坐標表示各泵頻率點上電磁流量計顯示的流量平均值(%)。


(1)各泵頻率點上計算得到的整周期FFT平均值隨著“泵頻率/流量”值的逐漸降低而減小。
(2)根據用戶手冊知道LUGB型渦街流量計所能檢測到的流體頻率范圍為13.191Hz~131.91Hz,這是該流量計用傳統的電路閾值方法處理渦街信號時的頻率檢測范圍。而用頻譜分析方法處理該流量計的渦街信號,在“泵頻率/流量”為35Hz/60.58%時得到的渦街信號頻率為11.0726Hz,比用傳統的電路閾值方法所能檢測到的下限頻率低2Hz左右。從這點看,頻譜分析方法處理渦街信號要比傳統的電路閾值方法優越,特別是在測量低流速段時。
(3)本實驗選取的采樣頻率為1kHz,采樣點數為2048點,因而頻率分辨率
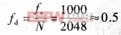
則系統在低流速時的測量相對誤差為

由此可見,若希望測量精度為0.45%,則在信號頻率不變的情況下,分辨率應該在0.05Hz以下,在采樣點數不變的情況下,則要求采樣頻率降低到100Hz以下,這就不能滿足香農采樣定理。若采樣頻率保持不變,要使分辨率在0.05Hz以下,則采樣點數需要增加到20480點以上。可是點數增加則增大數據存儲量,同時增大計算量,增加計算時間,會降低系統的實時性。而在采樣頻率和采樣點數一定的情況下,信號頻率越低,測量誤差越大。對此,用分段設置采樣頻率的辦法以達到同時滿足計算精度和系統實時性的要求。進行頻率分段,要進行采樣頻率的頻繁切換,這就很難實現在線的信號采集,也很難真正滿足系統的實時性,因此該方法不能從根本上解決問題。
(2)根據用戶手冊知道LUGB型渦街流量計所能檢測到的流體頻率范圍為13.191Hz~131.91Hz,這是該流量計用傳統的電路閾值方法處理渦街信號時的頻率檢測范圍。而用頻譜分析方法處理該流量計的渦街信號,在“泵頻率/流量”為35Hz/60.58%時得到的渦街信號頻率為11.0726Hz,比用傳統的電路閾值方法所能檢測到的下限頻率低2Hz左右。從這點看,頻譜分析方法處理渦街信號要比傳統的電路閾值方法優越,特別是在測量低流速段時。
(3)本實驗選取的采樣頻率為1kHz,采樣點數為2048點,因而頻率分辨率
則系統在低流速時的測量相對誤差為
由此可見,若希望測量精度為0.45%,則在信號頻率不變的情況下,分辨率應該在0.05Hz以下,在采樣點數不變的情況下,則要求采樣頻率降低到100Hz以下,這就不能滿足香農采樣定理。若采樣頻率保持不變,要使分辨率在0.05Hz以下,則采樣點數需要增加到20480點以上。可是點數增加則增大數據存儲量,同時增大計算量,增加計算時間,會降低系統的實時性。而在采樣頻率和采樣點數一定的情況下,信號頻率越低,測量誤差越大。對此,用分段設置采樣頻率的辦法以達到同時滿足計算精度和系統實時性的要求。進行頻率分段,要進行采樣頻率的頻繁切換,這就很難實現在線的信號采集,也很難真正滿足系統的實時性,因此該方法不能從根本上解決問題。
在低流速時,特別是當信號頻率在10Hz以下時,渦街信號和噪聲信號幾乎重疊在一起,甚至噪聲的幅值還略大于渦街信號幅值。此時,用功率譜分析方法來處理渦街流量信號,很可能得到的噪聲頻譜峰值要高于信號頻譜幅值,這樣就會將噪聲頻率錯認為是渦街信號頻率。由此看來,單純地用頻譜分析方法要達到擴展渦街流量計在低流速時的量程下限非常困難。
但是,利用頻譜分析能很好地展現信號的頻率分布特征,能初步提供渦街信號的頻率,為進一步進行渦街信號頻率的準確檢測做好了準備,提供了研究基礎和方向。在頻譜分析的基礎上,我們設計了渦街信號閾值處理專家系統,并已取得了一定的進展。下一步,我們將繼續結合譜分析,運用人工智能和專家系統的方法來處理渦街流量信號,以期能對擴展渦街流量計量程下限的問題有所突破。
但是,利用頻譜分析能很好地展現信號的頻率分布特征,能初步提供渦街信號的頻率,為進一步進行渦街信號頻率的準確檢測做好了準備,提供了研究基礎和方向。在頻譜分析的基礎上,我們設計了渦街信號閾值處理專家系統,并已取得了一定的進展。下一步,我們將繼續結合譜分析,運用人工智能和專家系統的方法來處理渦街流量信號,以期能對擴展渦街流量計量程下限的問題有所突破。







評論