控制系統中負反饋的數學原理是什么，如何用它來確保穩定性？

負反饋可以創建一個控制系統，其中過程的輸出用于抵消與所需設定點的任何偏差，有效地“糾正”系統，使其恢復平衡，并保持穩定運行。它用于各種應用，包括電壓調節、溫度控制器、音頻放大器和運算放大器。

本文簡要概述了在簡單穩壓器和更復雜的比例積分微分 （PID） 工業控制器中實現負反饋所涉及的數學運算，包括如何使用波特圖和奈奎斯特準則分析穩定性。

在負反饋回路中，反饋信號與輸入信號異相，有效地抵消了輸入信號本來會做出的任何變化。這與正反饋回路形成鮮明對比，在正反饋回路中，反饋信號與輸入信號同相并加強變化。

簡單控制系統和放大器的基本負反饋涉及一個反饋回路，其中輸出信號的一部分從輸入中減去。反饋環路增益 （A） 定義為 A = A?/（1 + βA?），其中 A? 是沒有任何反饋的開環增益，β 是反饋因數，表示發送回輸入端的輸出信號量。

在開關模式穩壓器的情況下，反饋用于調制占空比和控制輸出電壓。圖 1 說明了開關模式調制的基本原理。將反饋信號與誤差放大器中的參考電壓進行比較。接下來，將誤差放大器輸出與斜坡電壓進行比較，以控制開關時間。

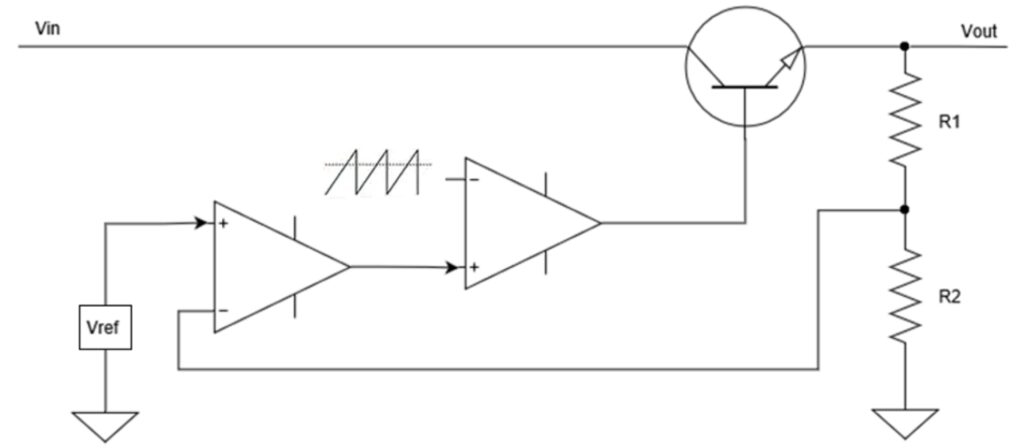
圖 1.開關穩壓器控制環路使用分壓器提供反饋信號。（圖片：Cadence)

PID 控制器可以在動態系統中提供穩健穩定的運行。它們也采用負反饋，但反饋計算更復雜，包括三個項，所有這些項都基于誤差信號。

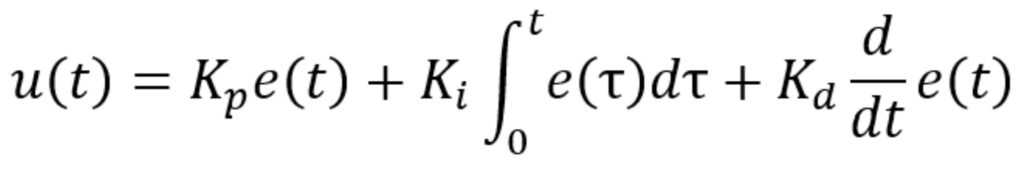
1. 比例項只是將電流誤差乘以常數 Kp.

2. 積分項將累積誤差乘以常數 K我.

3. 導數項將誤差的變化率乘以常數 Kd.

反饋回路的輸出 u（t），也稱為 e 或總誤差因子，被饋送到 PID 控制器中，以產生當前周期的控制信號 u（圖 2）。

圖 2.PID 控制系統和反饋回路的框圖。（圖片：Crystal Instruments）)

在復雜或高性能的控制應用中，環路內的相移會導致運行不穩定。

波特圖和穩定性

體圖和奈奎斯特穩定性準則適用于簡單的負反饋系統，例如具有單個控制參數的穩壓器和具有多個控制參數的復雜工業 PID 控制器。

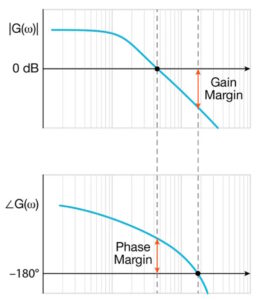
圖 3.波特圖可用于直觀地比較增益和相位裕量。（圖片：泰克）)

在波特圖中，反饋回路的增益和相位在縱軸上繪制，與頻率在橫軸上繪制。設計人員使用波特圖來確定增益裕量，它表示達到不穩定性所需的增益量，以及相位裕量，它表示達到不穩定性所需的相移量（圖 3）。

當相移接近 -180° 時，環路具有正增益 ≥ 1，并且可能會變得不穩定。波特圖為設計人員提供了一種簡單的方法來查看系統與該不良條件的接近程度。此外，通過對穩壓器施加突然的負載變化并觀察輸出電壓響應，設計人員可以評估動態條件下的環路穩定性。

奈奎斯特

奈奎斯特準則是穩定性分析的另一種工具。與分別顯示幅度和相位與頻率的波特圖不同，奈奎斯特圖將它們組合成一個復平面表示。

圖 4.穩定反饋系統的奈奎斯特圖示例。（圖片：IEEE Open Journal of Power Electronics)

這是一種用于分析開環傳遞函數頻率響應的圖形技術，利用拉普拉斯變換將時域中的積分和導數轉換為 s 域中的簡單乘法和除法（圖 4）。

總結

本文介紹了負反饋的數學原理，應用于各種系統，包括穩壓器、溫度控制器和復雜的工業過程。它還考慮了如何使用波特圖和奈奎斯特準則來分析反饋和控制系統的穩定性。