韋弗法單邊帶信號產生方法簡介
了解韋弗調制器,這是一種射頻電路,它通過去除對陡峭帶通濾波器或正交移相器的需求,改進了舊式的單邊帶調制方法。單邊帶(SSB)調制是一種幅度調制(AM),它使用上邊帶或下邊帶來傳輸信息。與其他形式的幅度調制相比,SSB調制的主要優勢是節省帶寬和功率。本系列的前幾篇文章討論了單邊帶信號生成的濾波法和移相法。現在,我們將探討第三種選擇:韋弗調制器。
本文引用地址:http://www.104case.com/article/202505/470378.htm“第三種方法”
濾波法是最古老、最直接的單邊帶調制形式。然而,它需要具有極陡過渡區域的帶通濾波器。自1924年引入以來,移相法——消除了這一需求——被認為顯著優于前者。如圖1所示,移相法通過在調制器輸入端使用移相網絡來生成單邊帶信號。
圖1. 使用移相法生成單邊帶信號。
在該方法中使用的移相網絡必須生成彼此精確相差90度的信號。雖然比上述的陡峭帶通濾波器更容易實現,但這些移相網絡的實現也并非易事。盡管如此,移相法仍然是主要的方法,直到20世紀50年代末。1956年,唐納德·K·韋弗在一篇題為《單邊帶信號的第三種生成和檢測方法》的論文中引入了一種新方法。這種方法摒棄了對陡峭帶通濾波器或精確移相器的需求。相反,韋弗用正交變頻過程替換了移相法中的正交移相器。韋弗調制器(圖2)使用了四個乘法器和兩個低通濾波器。
圖2. 韋弗法生成單邊帶信號。
請注意,圖2顯示的是保留上邊帶(USB)的配置。在本文后面,我們將探討如何修改電路以生成下邊帶(LSB)。在韋弗電路中,所需的90度相位差是由第一組乘法器和低通濾波器共同產生的。韋弗電路中的第二組乘法器與移相法中的工作方式相同,只是它們使用了不同的本振頻率。電路中的第一對乘法器使用一個頻率為f0的振蕩器將消息信號下變頻,該頻率位于消息信號頻率范圍的中心。如果消息信號的頻率范圍為fa≤f≤fb,則應用于第一對乘法器的載波為:
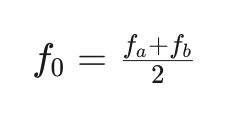
公式1
經過下變頻后,消息信號的中心頻率變為直流(f=0)。得到的信號隨后通過低通濾波器,其截止頻率為:
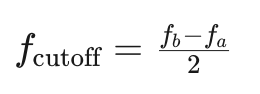
公式2
如果所需的載波頻率為 fc,則第二對乘法器必須由頻率為 fc+f0 的振蕩器驅動。
將單頻輸入信號應用于韋弗調制器
讓我們使用圖3來分析電路對單頻消息信號 m(t)=cos(ωmt) 的響應。
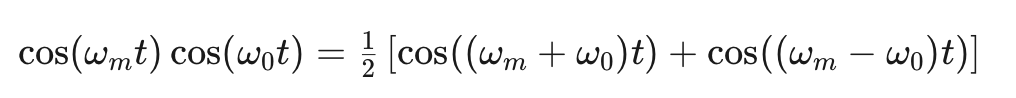
公式3
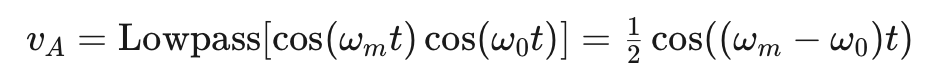
公式4
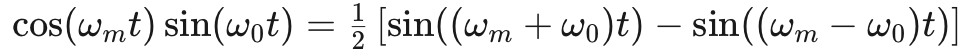
公式5
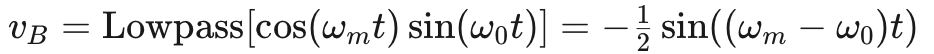
公式6
公式4和公式6表明,低通濾波器的輸出信號之間存在90度的相位差。正如我們之前提到的,實現這種相位差是移相法的關鍵挑戰。現在我們已經準備好找到調制器的輸出信號。使用 vA 和 vB,韋弗調制器的輸出信號為:
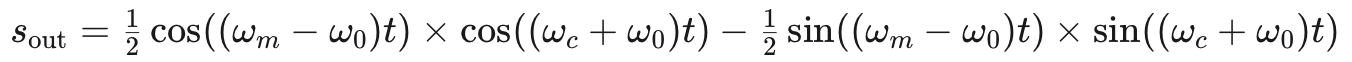
公式7
我們可以通過識別其與以下三角恒等式的相似性來簡化這個表達式:
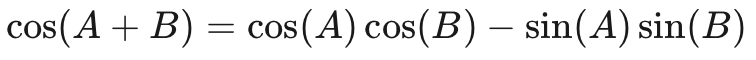
公式8
應用這個恒等式,輸出信號簡化為:
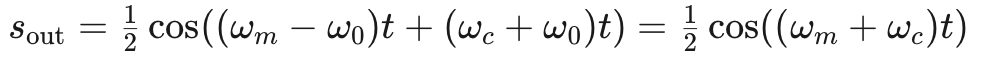
公式9
該信號的頻譜由位于 ±(fc+fm) 的兩個沖擊組成。這些對應于圖4中的上邊帶分量。
生成下邊帶信號
到目前為止,我們僅使用韋弗調制器生成了上邊帶信號。然而,通過改變特定項的極性,我們可以消除上邊帶并生成下邊帶信號。圖5展示了所需的調整。
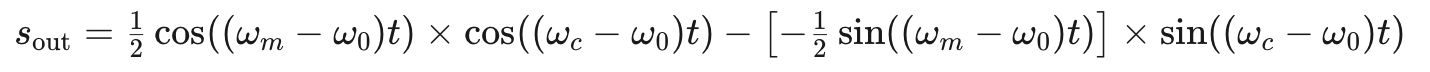 公式10
公式10
簡化為:
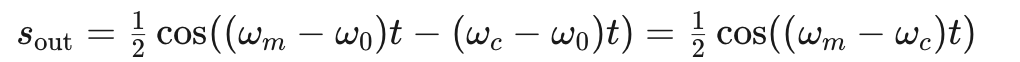
公式11
該信號的頻譜由位于 ?fc+fm 和 fc?fm 的兩個沖擊組成,對應于下邊帶分量(見圖4)。
使用復基帶表示法理解韋弗法
在前一篇文章中,我們學習了帶通信號的復基帶表示。讓我們簡要回顧一下與當前討論相關的這一概念的關鍵方面。這將使我們能夠通過從另一個角度來檢查韋弗調制器,從而加深對其的理解。考慮一個以固定射頻頻率 fc 為中心的調制正弦波,其幅度和相位變化緩慢:
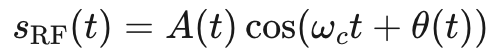
公式12
其中 A(t) 和 θ(t) 分別是時變信號的瞬時幅度和相位。上述公式可以重寫為:
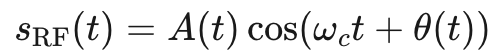
公式13
方括號內的項是信號的復基帶表示:
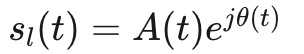
公式14
上述公式也可以用笛卡爾形式表示:
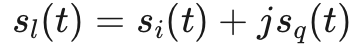
公式15
其中 si(t) 和 sq(t) 是 sl(t) 的實值同相分量和正交分量。從公式14和公式15中,我們得到同相分量和正交分量的值:

公式16
這一分析表明,帶通信號可以分解為兩個相差90度的低通信號。相關問題是:如何為給定信號生成 si(t) 和 sq(t)?為了找出答案,讓我們將注意力重新轉向電路。
韋弗調制器的構建模塊
正如我們在前一篇文章中討論的,基帶表示的同相分量和正交分量可以通過一對乘法器和低通濾波器獲得。該電路如圖6所示。此外,如果我們有同相分量和正交分量,我們可以使用圖7中的配置重建帶通信號。圖6和圖7中的電路是韋弗調制器的構建模塊。
在組合電路中,兩對乘法器由不同的本振頻率驅動。例如,第一對乘法器由 f0 驅動,而第二對乘法器由 fc+f0 驅動,用于上邊帶生成。如果兩對乘法器使用相同的振蕩器頻率,則電路實際上會在輸出端復現消息信號。通常,在討論復基帶表示的概念時,輸入是一個射頻信號。然而,韋弗電路將這一概念應用于基帶信號。韋弗調制器通過下變頻消息信號來找到其同相分量和正交分量。





評論