噪聲系數概念——功率增益、損耗分量和級聯系統
噪聲因子的概念相當直觀,它用于表征信號通過組件時信噪比(SNR)的劣化。然而,噪聲系數定義中隱藏著一些微妙之處,有時沒有得到足夠的強調。必須充分理解的一個復雜之處是,在290 K的標準溫度下,噪聲系數值是為已知的源電阻(通常為50Ω)指定的。
在本文中,我們將討論另一個重要的微妙之處,即噪聲系數定義中使用的功率增益類型。之后,我們將研究有損組件以及級聯系統的噪聲系數。
重新審視噪聲系數定義和信噪比
噪聲因子(F)定義為輸入端的信噪比與輸出端的信信噪比之比:
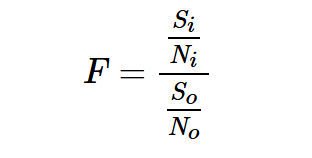
方程式1
解釋:
Si和So是電路輸入和輸出端的可用信號功率
Ni和No是輸入和輸出端的可用噪聲功率
將So=GASi替換為以下方程式:
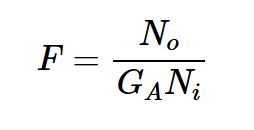
其中GA是電路的可用功率增益。
接下來,讓我們來看看可用功率增益的定義。
使用阻抗的模塊的可用功率增益
圖1說明了如何計算給定源阻抗ZS=RS+jXS的模塊的可用功率增益。
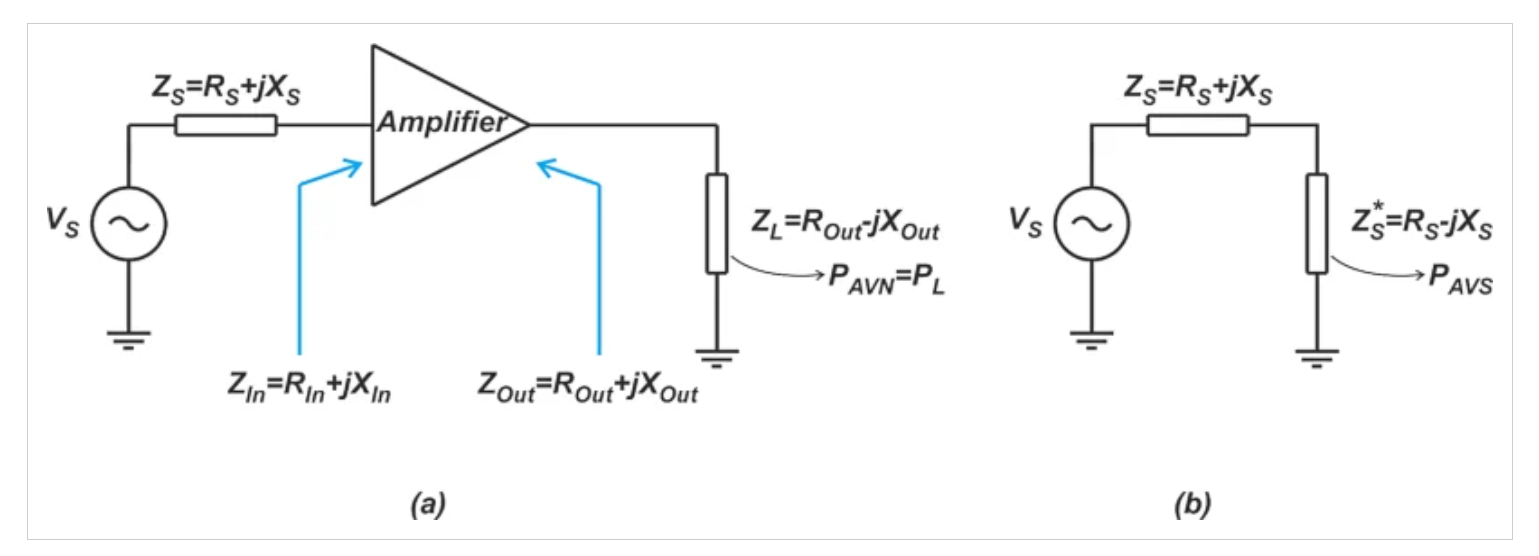
圖1顯示給定源阻抗下模塊功率增益的圖
假設模塊的輸入和輸出阻抗為ZIn=RIn+jXIn,Zout=Rout+jXout。如圖1(a)所示,我們可以將模塊輸出連接到共軛匹配負載,即ZL=Rout-jXout,并測量輸送到負載的功率PL。由于輸出是共軛匹配的,PL是網絡PAVN的可用功率。
所需的另一個量是電源PAVS的可用功率。這是源傳遞給ZS復共軛體的功率,如圖1(b)所示。PAVN與PAVS的比率定義為模塊GA的可用功率增益:
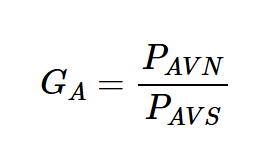
可用增益取決于ZS,而不是ZL。這是因為根據定義,負載阻抗是模塊輸出阻抗的復共軛匹配,因此已經由模塊的輸出阻抗設置。請記住,可用增益解釋了DUT(被測設備)的源和輸入之間的不匹配。
在噪聲系數定義(方程式1)中,Si是信號源的可用功率,So是可以傳遞到匹配負載的輸出功率。因此,So/Si比值符合可用功率增益的定義。請記住,射頻工作中有幾種不同的功率增益定義,如換能器功率增益和插入功率增益。如果我們在NF計算中使用可用增益以外的功率增益,我們將獲得實際NF值的近似值。例如,實際的噪聲系數測量方法通常決定DUT的插入增益。使用插入增益而不是可用增益可能會在我們的噪聲系數測量中引入誤差。
同樣值得一提的是,在處理級聯階段時,可用增益是有用的。級聯的總可用增益等于單個可用增益的乘積。為了找到級聯的可用增益,應為等于前一級輸出阻抗的源阻抗指定每級的可用增益。
有損組件的噪聲系數
在設計射頻系統時,我們偶爾會發現有必要在信號鏈的特定點引入損耗。例如,在測試和測量應用中,我們可以通過衰減器降低失配不確定性。衰減信號的無源電路必須具有物理電阻,我們知道電阻會產生熱噪聲。因此,無源衰減器會降低信噪比性能。讓我們看看如何確定這些組件的噪聲系數。例如,考慮為50Ω系統設計的6 dB T型衰減器,如下圖所示(圖2)。
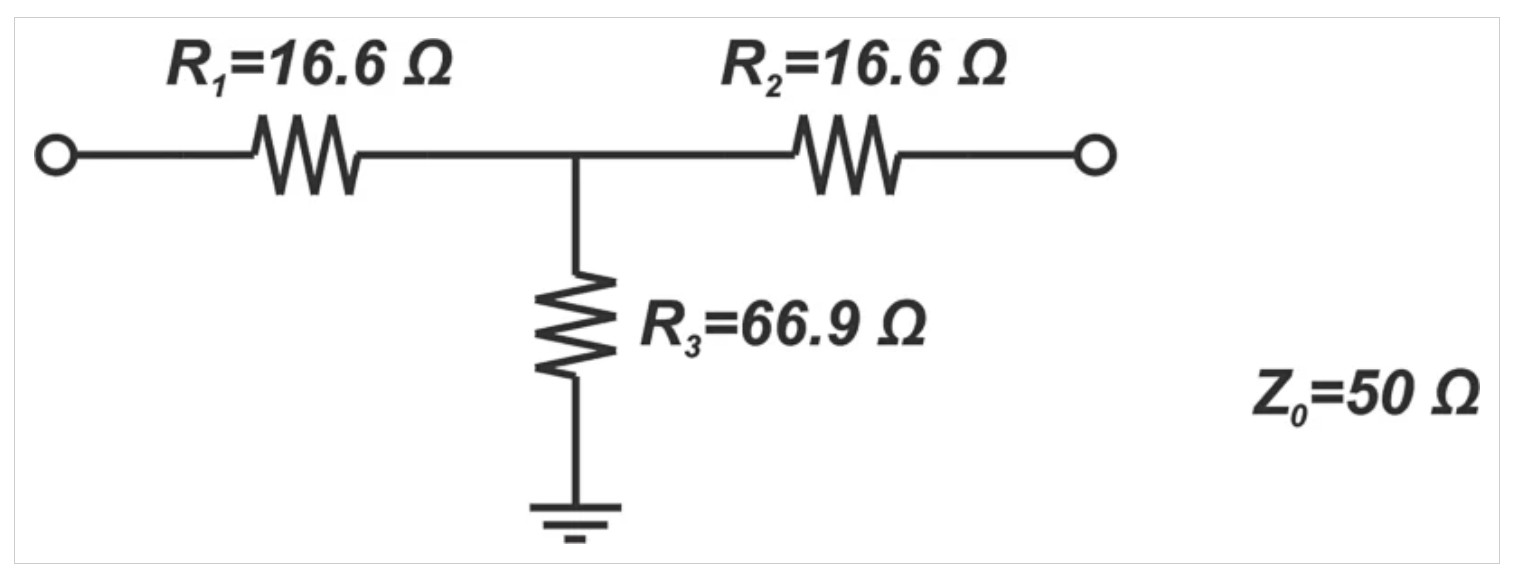
圖2為50Ω系統設計的6 dB T型衰減器的示例圖
我們可以遵循一般程序,通過執行噪聲分析來確定該電路的噪聲系數。這種方法涉及一些繁瑣的計算。一種更有效的方法是考慮電路的戴維南等效。衰減器輸出端的可用噪聲是衰減器戴維南電阻的可用噪聲。一般來說,如果無源(互易)網絡的兩個端子之間的戴維南電阻等于Rth,則這些端子之間的熱噪聲PSD由下式給出ˉˉˉˉˉˉˉV2n=4kTRthBVn2ˉ=4kTRthB.
在我們的例子中,衰減器是為50Ω系統設計的。添加輸入和輸出端子,我們得到如圖3所示的以下示意圖。
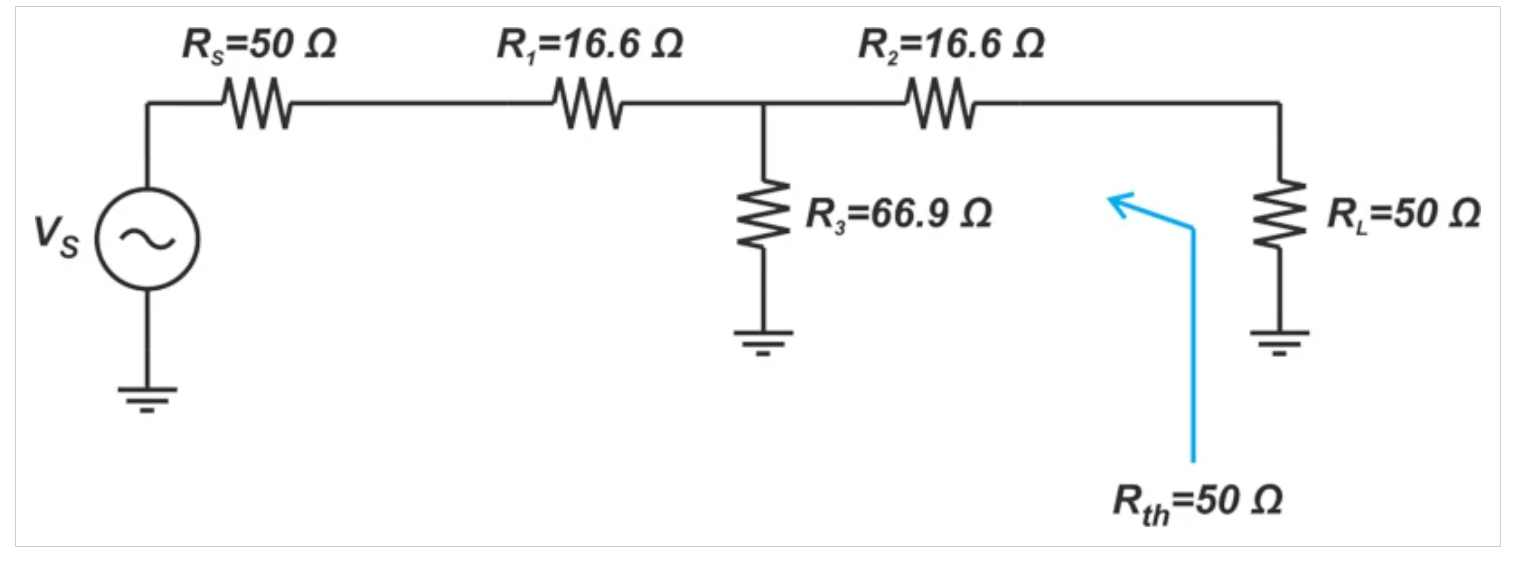
圖3顯示50Ω衰減器以及輸入和輸出端子的示意圖
根據設計,輸出阻抗Rth等于系統的參考阻抗,即Rth=50Ω。由于Rth等于源阻抗Rs,衰減器輸出端可用的噪聲功率等于源阻抗Rs提供的噪聲功率(我們隱含地假設衰減器和Rs處于相同的溫度)。這意味著衰減器輸入端和輸出端的噪聲功率相同,或者方程1中的Ni=否,這導致:
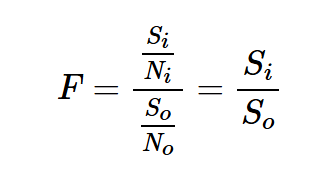
另一方面,我們知道衰減器按其指定值衰減輸入信號功率。例如,對于6dB衰減器,Si比So大6dB。考慮到這一點,上述方程表明6dB衰減器的噪聲系數為6dB。一般來說,如果無源衰減器的物理溫度為T0=290K,則其噪聲系數(dB)等于其損耗(dB)。
如果我們分析圖3中的電路,我們會發現Rs產生的噪聲在通過衰減器時衰減了6dB。然而,電阻器R1、R2和R3對電路輸出貢獻的噪聲剛好足夠,使得衰減器輸入和輸出處的總可用噪聲相同。
如果衰減器處于任意溫度怎么辦?
上述討論僅適用于衰減器處于T0的情況。如果衰減器處于任意溫度T,我們可以首先考慮衰減器和源電阻都處于T的情況。通過分析這種情況,我們可以確定衰減器No(添加)添加的噪聲,并可以使用此信息找到噪聲系數。讓我們以圖3中的電路為例進行檢查。如果包括Rs在內的整個電路處于T,則輸出No處的可用噪聲功率等于Rs的可用噪聲能量(我們知道它是kTB):
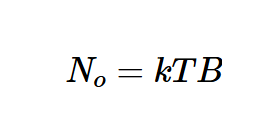
我們可以通過另一個方程找到總輸出噪聲No:
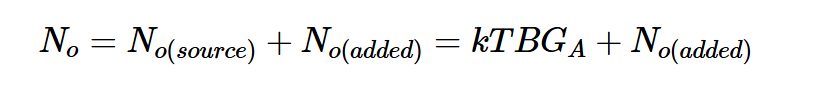
解釋:
No(源)是源阻抗產生的輸出噪聲的一部分
否(添加)是衰減器添加的噪聲
GA是塊的可用增益
結合這些方程,我們可以找到No(added)=kTB(1-GA)。現在,如果我們假設Rs處于噪聲系數定義指定的標準溫度T0,則T處有損分量的噪聲系數為:
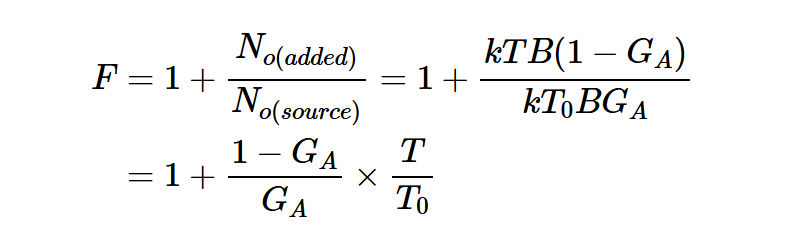
對于衰減器,損耗L等于1/GA,上述方程可以簡化為:
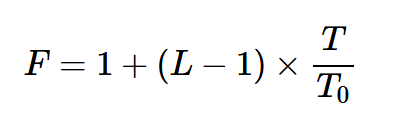
在T=T0的特殊情況下,我們得到F=L,這與我們在上一節中的討論是一致的。
級聯系統的噪聲系數
雖然我們通常單獨描述電路塊,但我們最常用它們作為級聯系統的組成塊。因此,根據各個塊的噪聲系數規格來確定整個系統的噪聲性能非常重要。考慮一個由N個雙端口設備組成的級聯系統,如圖4所示。
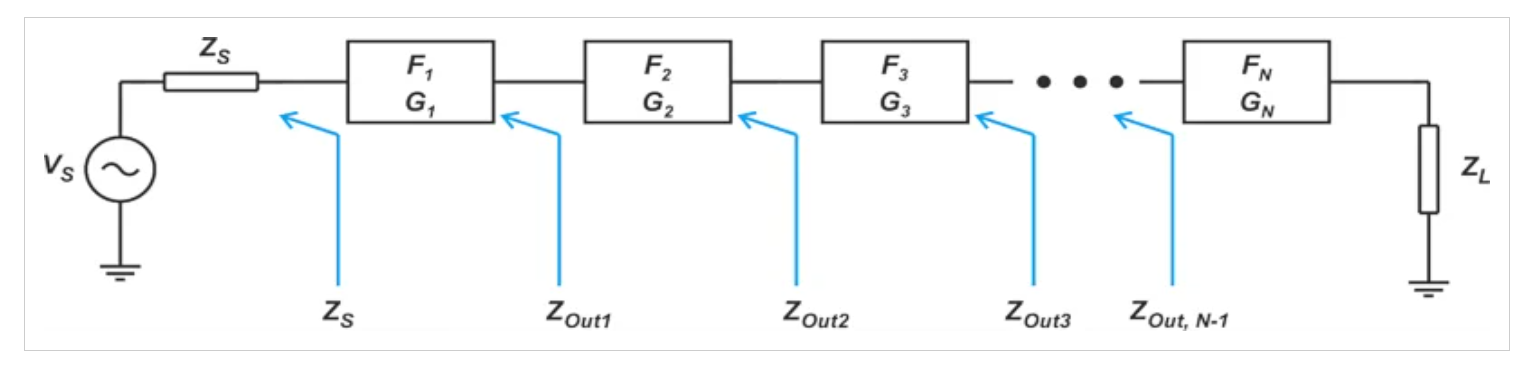
圖4由N個雙端口設備組成的級聯系統示例
在上圖中,Fi和Gi表示第i級的噪聲因子和可用功率增益。級聯系統的噪聲系數可以通過應用以下方程(稱為Friis方程)來計算:
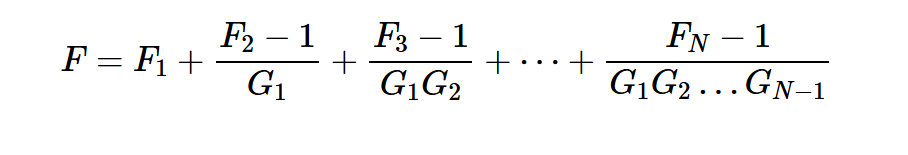
注意,在上述方程中,Fi和Gi項都是線性(不是對數)量。根據Friis公式,每個階段的噪聲系數除以該階段之前的總增益。因此,后期階段對整體性能的影響較小。這意味著第一階段對整個系統的噪聲系數有重大影響。
在上一篇文章中,我們討論了為給定的源阻抗指定噪聲因子度量。在處理Friis方程時,應該注意的是,應為前一級的輸出阻抗指定每級的噪聲系數。例如,參考圖4,應為Zout1的源阻抗指定第二級F2的噪聲因子,F3對應于Zout2的源阻抗,以此類推。讓我們看一個例子來澄清上述一些概念。
示例:查找無線接收器前端的噪聲系數
找到以下無線接收器前端的噪聲系數,如圖5所示。
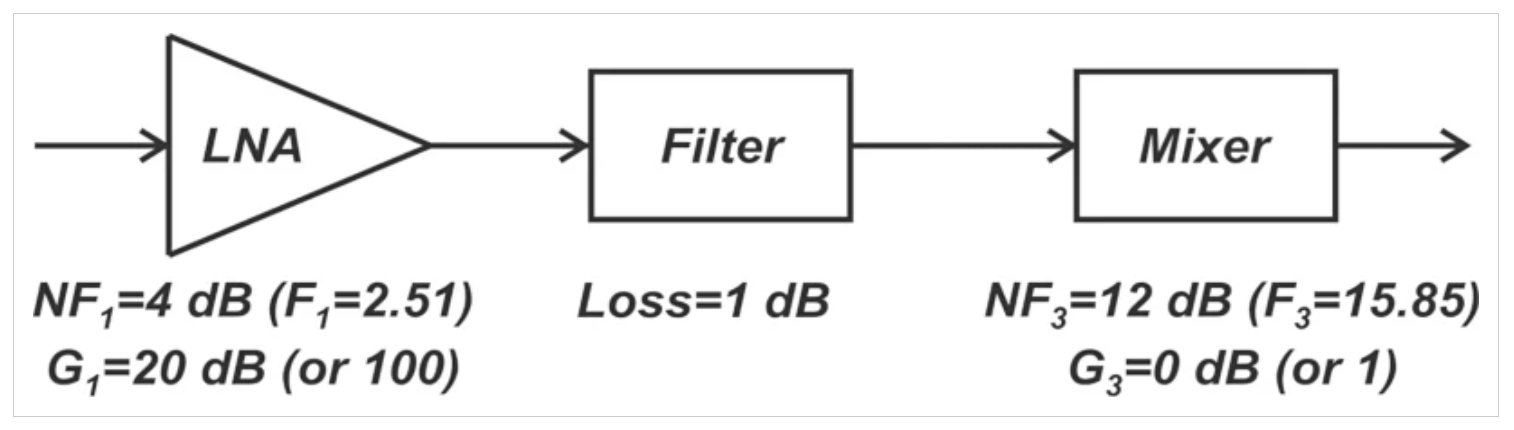
圖5來自終端系統的示例無線接收器
LNA和混頻器的噪聲系數和增益也如圖所示。此外,濾波器的損耗為1 dB。我們知道,無源衰減器的噪聲系數(dB)等于其損耗(dB)(假設物理溫度T0=290 K)。因此,對于過濾器,我們有:
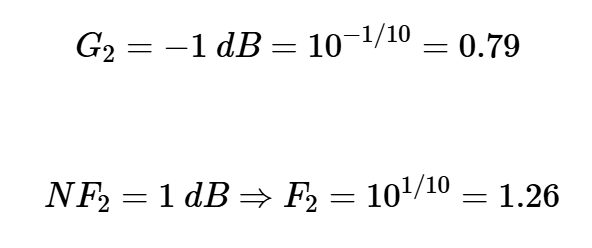
應用Friis方程,我們有:
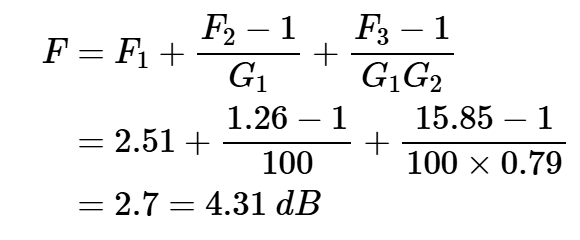
雖然混頻器本身具有F3=15.85的較大噪聲因子,但添加濾波器和混頻器會使整體噪聲因子增加一個相對較小的值,從2.51增加到2.7。濾波器和混頻器的貢獻很小,因為相對較大的增益先于這些組件。
分立與集成射頻設計
Friis的方法最適合離散射頻設計,其中每個塊的輸入和輸出阻抗與參考阻抗(通常為50Ω)相匹配。在集成射頻系統中,不同模塊的輸入/輸出阻抗通常未知且不同;并且通常不嘗試在級之間提供阻抗匹配。在這些情況下,弗里斯的方程式變得繁瑣;通過計算不同噪聲源的貢獻,可以更容易地直接找到噪聲系數。在本系列的下一篇文章中,我們將對此進行更詳細的討論。



評論