基于FPGA的數字信號處理--什么是定點數?
在實際的工程應用中,往往會進行大量的數學運算。運算時除了會用到整數,很多時候也會用到小數。而我們知道在數字電路底層,只有「高電平1」和「低電平0」的存在,那么僅憑 0和1 該如何表示小數呢?
本文引用地址:http://www.104case.com/article/202405/458588.htm數字電路中,小數可以用兩種形式來表示:「定點數」和「浮點數」。浮點數的內容我們下篇文章再講,本文只講定點數。
什么是定點數?
首先要明確的是,「定點數」的說法是相對「浮點數」來說的。要理解什么是定點數,可以先從要理解它的名字開始–定是什么?點又是什么?
「定點數」是英語「fixed-point number」的中文翻譯,fixed的意思是固定的,point的意思是小數點,所以「定點數」其實也可以叫「固定小數點的數」。同樣的,「浮點數」自然就是「浮動小數點的數」。
在10進制中,小數的表示是通過小數點和它所在位置來實現的。比如12.5,它表示的值是十二點五;而1.25則是一點二五。盡管12.5和1.25都用了「1 2 5」這3個數來表示,但由于小數點位置的不同,使得前者的數值是后者的十倍。
遺憾的是,電路只能表示1和0,無法直接表示小數點,所以上面的方法在電路中是行不通的。
假如你現在收到一條信息「我傳一個小數過來,10100111」,看到這樣一條信息,你恐怕只會覺得莫名其妙!10100111是哪門子小數?慢著,10100111如果直接轉換成10進制數就是167,167當然不是小數,因為它沒有小數點。但是仔細想想?它真的沒有小數點嗎?如果把167看做是167.0呢?也就是默認它的小數點是在最右邊呢?

接著你很快又收到了第二條信息「我再傳一個小數過來,10100111,它的小數點在從右往左數第1位」。這次你終于能看懂了 ,這不就是1010011.1嗎?也就是10進制數83.5。那么直接說83.5不就完事了嗎?說這么多干嗎?

然后是第三條消息「我再傳一個小數過來,10100111,它的小數點在從右往左數第2位」。這次傳的是101001.11,即10進制數41.75。

······(省略后面的10086條消息)······
看到這是不是清晰很多了–盡管我們無法直接用小數點來表示2進制小數,但可以通過指定小數點的位置來說明這是一個小數啊!
約定小數點的位置,且這個位置固定不變,小數點前、后的數字,分別用2進制表示,組合起來就可以用來表示和使用2進制小數了。用這種方式表示的數就叫做「定點數」。
定點數如何表示數字?
很容易想到,定點數除了能表示小數外,也可以表示整數。因為你可以把小數點的位置約定在最右面,這樣其實相當于沒有小數點,所以表示的都是整數;同樣的,你也可以把小數點規定在最左邊,這樣表示的就是一個整數部分為0的小數。
所以定點數的表示可以分為三種情況:
純整數
這種情況約定小數點在最右邊。例如10進制數85用8位無符號2進制數表示就是0101_0101,因為小數點在最右邊,所以可以看做是0101_0101.0 。

純小數
定點純小數是指整數部分為0的小數。根據是無符號數還是有符號數,分為兩種情況:
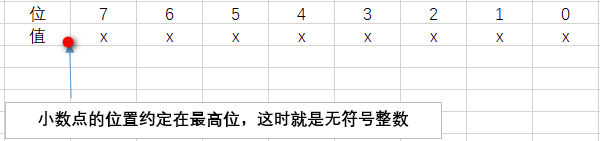
(1)無符號數
無符號數的最高位不表示符號,僅表示數值。這種情況約定小數點的位置在最左邊。例如10進制數0.125用8位無符號2進制數表示就是0.0010_0000,因為小數點在最左邊,所以是0010_0000。
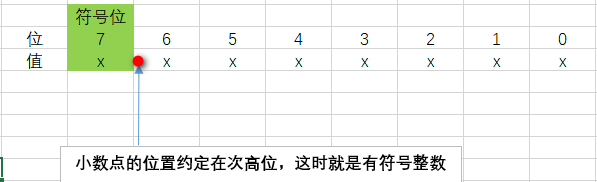
(2)有符號數
有符號數的最高位表示符號,不表示數值。這種情況約定小數點的位置在次高位。例如10進制數-0.125用8位無符號2進制數表示就是1.0010_000,因為小數點在次高位,所以是1010_0000。
整數 + 小數
除了純整數和純小數這兩種情況外,其實定點數主要是用來表示 「整數 + 小數」的情況,例如3.14、1.5、25.125等等。這種情況需要確定以下信息才能正確表示該數:
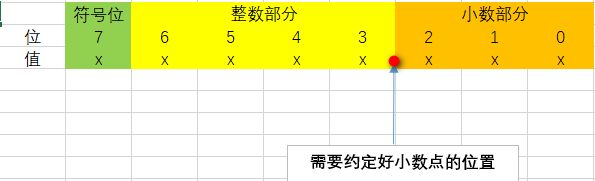
整數和小數的長度之和確定了用多大的電路來表示定點數,而二者的長度之比則確定了小數點的位置。符號位則確定了該數是一個有符號數還是一個無符號數。
光說不練云玩家,接下來看幾個例子。
(1)1.25 的定點數表示
首先約定用無符號數來表示,然后約定5 位為整數部分,3 位為小數部分。所以有:
1.25(D) = 1.01(B) = 00001.010 = 000010101
(2)-9.5 的定點數表示
首先需要用有符號數來表示,因為整數9需要4位來表示,而小數0.5僅需1位就可表示。為此可以約定5位為整數部分(注意最高位為符號位),3 位為小數部分。所以有:
-9.5(D) = 10110.1(B) = 10110.100 = 101101001
定點數的數值范圍
定點數用來表示小數很方便,但是它也有個很大的問題–它的表示范圍很小。
以5 位表示整數部分,3 位表示小數部分的無符號定點數為例,它的整數部分可以表示的范圍是00000-11111,即0-31,步長是1;小數部分的范圍是0.000-0.111,即0-0.875,步長是0.125。綜合起來范圍是0-31.875,步長為0.125。
有符號數的因為是用補碼表示,所以它的范圍取值比較特殊。以5 位表示整數部分,3 位表示小數部分的有符號定點數為例,它能表示的最小值是10000_000,即-32,它能表示的最大值是01111_111,即15.875。
若以m表示定點數的整數位寬(m不包含符號位),以n表示定點數的小數位寬,則有符號數和無符號數的定點數的表示范圍為:
| 有符號數 | -2^m ~ (2^m - 2^-n) |
|---|---|
| 無符號數 | 0 ~ (2^m - 2^-n) |
如果想表示更大范圍、更高精度的值,怎么辦?
一些定點數的表示格式
除了可以用類似「以5 位表示整數部分,3 位表示小數部分的無符號定點數」的語言來描述定點數的格式外,還有多種定點數的表示格式。常見的有以下幾種:
Q格式(Q notation)
Q格式的一般形式是:
Qm.n
默認情況下,用Q格式描述的都是有符號定點數。其中m表示整數部分的長度(這個值不包括符號位),n表示小數部分的長度。所以用Q格式描述的定點數的整體長度為:
w = m + n + 1 //整數部分長度 + 小數部分長度 + 符號位長度
例如 「 Q3.12 」描述的是一個整體長度為16位的2進制有符號定點數,它的整數部分長度是3,而小數部分長度是12。根據小數部分的長度,可以推斷出分辨率為 2^-12。
在Q前面加一個 U 即可用來表示無符號的2進制定點數。例如 「 UQ1.15」描述的就是一個整數部分長度為1,小數部分長度為15的無符號的2進制定點數。
整數部分的長度值和小數點可以被省略,而只描述小數部分的長度。例如「 Q12 」描述的就是一個小數部分長度是12的2進制有符號定點數,但是它的整體長度是不確定的,你可以額外指定整體長度,或者說整體長度就取決于存儲這個定點數的寄存器。
如果這個定點數存儲一個16位的寄存器,那它的值就是:
xxxx . xxxx_xxxx_xxxx
如果這個定點數存儲一個32位的寄存器,那它的值就是:
xxxx_xxxx_xxxx_xxxx_xxxx_xxxx . xxxx_xxxx_xxxx
其實也可以看出來,這種表示方法就是把它的值乘以 2^-12 。
這種整數長度m不包括符號位的Q格式主要是TI公司的DSP在使用,ARM公司也有一種類似的Q格式,但是它的整數長度m是包含符號位的。表示方式的不同不是什么大不了的事,只要是使用過程中確定好了就行,為此你甚至也可以自己創造一套定點數表示方式(只要不怕沒人用就行,嘿嘿)。
S表示法
S表示法的一般形式是:
Sm.n
其中S表示這是一個有符號的定點數,m表示整數位數(m不包括符號位),n表示小數位數。這種方法其實跟Q格式很像,只不過它的表示無符號定點數的方法不是在前面加 U ,而是去掉 S,像這樣:
m.n
例如「 2.4 」表示的就是一個整數位數為2,小數位數為4的無符號定點數。
總結
總的來說,用定點數表示的小數,不僅數值的范圍表示有限,而且其精度也很低。要想解決這 2 個問題,人們就提出了使用「浮點數」的方式表示數字,關于浮點數的表示方法,我們會在下一篇文章進行講解。
定點數和浮點數都可以表示小數,而定點數的精度固定,表現范圍比較有限;但是,定點數在硬件上比較容易實現,在實際的數據算法中,定點數運算效率比浮點數的運算效率高很多,同時定點數使用的資源也比較少。因此,定點數被廣泛地應用在數字信號處理的各種應用場景中。















評論