利用FPGA進行基本運算及特殊函數定點運算
一、前言
本文引用地址:http://www.104case.com/article/202402/455484.htmFPGA以擅長高速并行數據處理而聞名,從有線/無線通信到圖像處理中各種DSP算法,再到現今火爆的AI應用,都離不開卷積、濾波、變換等基本的數學運算。但由于FPGA的硬件結構和開發特性使得其對很多算法不友好,之前本人零散地總結和轉載了些基本的數學運算在FPGA中的實現方式,今天做一個系統的總結歸納。
二、FPGA中的加減乘除
1.硬件資源
Xilinx 7系列的FPGA中有DSP Slice ,叫做“DSP48E1”這一專用硬件資源,這是一個功能強大的計算單元,單就用于基本運算的部分有加減單元和乘法器。詳見參考文獻1.
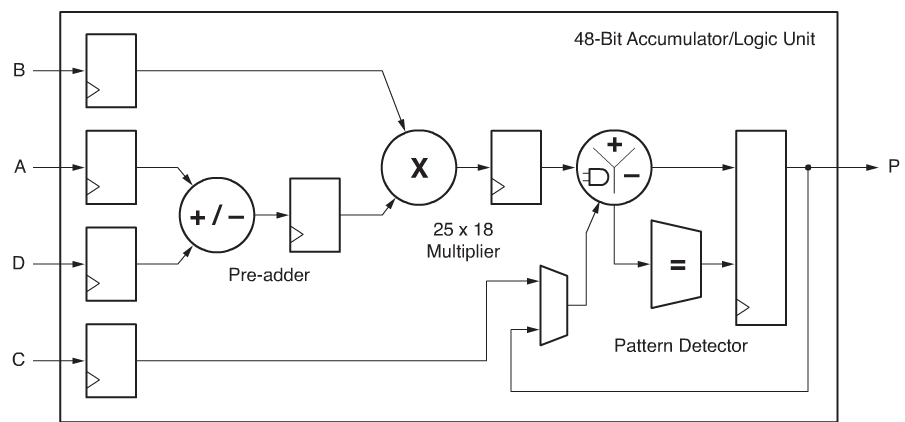
因此可以直接用HDL語言中的加、減、乘符號實現變量與常量間運算操作以及變量與變量間操作。而四則運算中的除法沒有基本的邏輯計算單元可以對應,因此計算除法需要調用除法器IP核。
2.確認數據的表示范圍
有符號數:(補碼)-2^(N-1) ~ 2^(N-1)-1 如N = 8,則表示范圍是:-128 ~ 127.
無符號數:0~2^N-1 如N = 8,則表示范圍是:0~255.
定點數:2Q13 范圍是:-4~4-2^(-13) 精度是:2^(-13)
3.結果有效位寬
首先討論結果位寬問題。在FPGA中往往采用定點運算替代浮點運算來降低硬件資源占用率和計算延遲,其中的精髓就是精度與資源的權衡。若按照保留計算結果的全部精度,N bit數與Mbit數相加結果需要N+1bit(N>M)。N bit數與M bit數相乘之積需要N+M bit。而減法可以轉化為加法,除法則轉換為乘法和加減法的組合。如果操作數是定點小數,則在滿足以上準則的前提下,A與B相加(A小數點位數>B小數點位數),結果小數點位數與A相同;A與B相乘(小數點位數分別為p和q),結果小數點位數是p+q。
4.定點運算步驟
然而(話鋒一轉),在大多數場合下,不需要以上這么多位來保留計算結果,因為我們在進行數學運算時,已經知道輸入數據的大致范圍,一個數除以1000和除以1結果數據所需最小位寬能一樣么?加減運算的操作步驟是先對齊小數點位數,后加減。而乘法是先計算后取小數點。這實際上與十進制運算一致,我們看看具體的計算步驟:
整數之間加減以及乘法的統一步驟:預估結果位寬N --> 按照結果位寬擴展操作數符號位以防止溢出 --> 運算取低N位。
定點小數加減運算步驟:預估結果位寬N --> 得到結果小數點后位數 --> 對齊操作數整數位和小數位,確定擴展位寬M(M≥N) --> 加減運算取低M位。
定點小數乘法運算步驟:預估結果位寬N --> 得到結果小數點后位數 --> 擴展操作數位寬 --> 相乘取低N位
5. 變量與常量運算化簡
以上討論的均是兩變量之間的運算規則,當然結果位寬及格式準則是適用的。變量與常量的運算的優勢在于,可以將乘除法轉換成加減以及移位運算實現,從而降低計算復雜度和延遲。當常數項C為2的整數次冪(C = 2^p),則乘C等于變量左移p位,除以C等于變量右移p位。幾個在書中看到的幾個簡單示例:A*16 = A <<4 A*20 = A<<4 + A<<2. A除以2 = A >>1 A除以3 = A*(0.25+0.0625+0.0156) = A>>2+A>>4+A>>6 A除以5 = A*(0.125+0.0625+0.0156) = A>>3 + A>>4 + A>>6.其中乘法完全等價對應的移位相加操作,而除法的移位代替會損失精度。
三、如何計算特殊函數
FPGA內部的DSP Slice可以直接進行最基本的加法和乘法運算,但是對于其他比如對數、指數、三角函數、開根號等特殊函數就無能為力了。這時需要借助算法對這些特殊函數進行變換和簡化。FPGA實現復雜函數的常用手段一個是級數展開,再一個就是CORDIC算法。關于CORDIC的理論知識和具體內容詳見參考文獻2,這里主要闡述CORDIC的IP核調用以及應用示例。CORDIC算法就是通過一定的手段,將很多復雜的特殊函數變為相加移位運算,這一點對于硬件芯片實現來說非常友好。CORDIC分為旋轉模式和矢量模式,配合圓周坐標、線性坐標和雙曲線坐標會有六種組合,具體見下表:

從表中發現,基本的乘

除法、三角函數、反三角函數、雙曲函數、反雙曲函數、開根號都能夠直接求得,那其他函數怎么辦?
常見的函數計算需求基本都能滿足,雖上述變換式對自變量定義域有限制,但同樣可以分析輸入數據的取值范圍并利用簡單的數學變換得到想要的結果。Xilinx同時提供了浮點IP核以及CORDIC IP核,前者調用簡單但占用資源大,延遲高,因此利用CORDIC算法計算函數是個較好的選擇。
四、CORDIC計算e^x Demo
1. 算法仿真分析
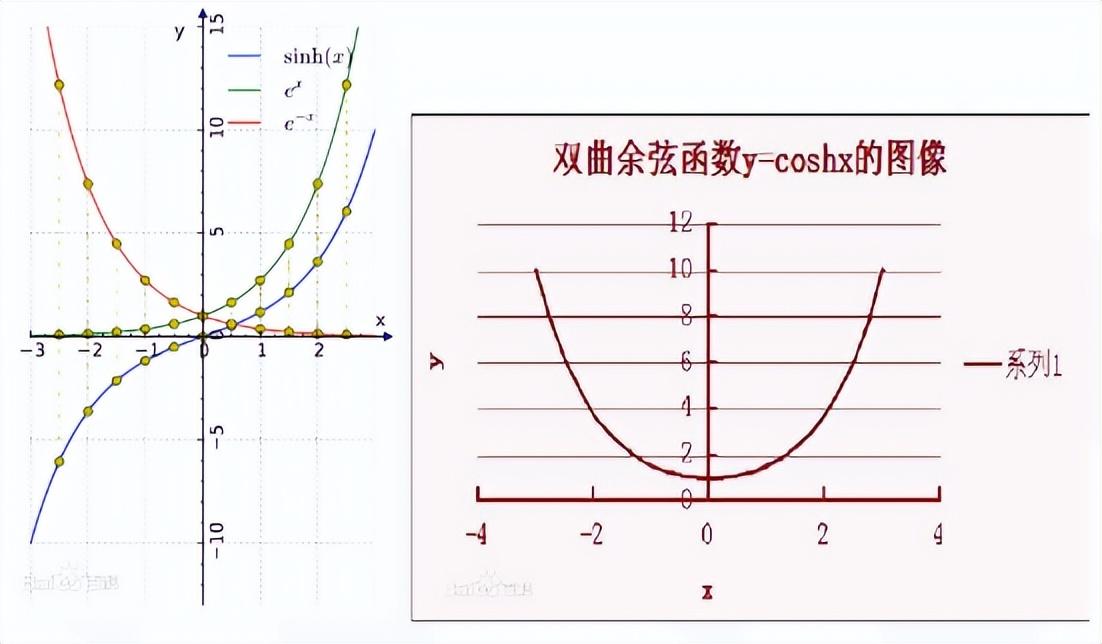
要計算e^x數值需要讓CORDIC工作在雙曲坐標的旋轉模式下,通過e^x = sinhx+coshx關系式間接求得。首先看下sinh和cosh函數的曲線,有個直觀認識。
我們用MATLAB毫不費力地驗證一下公式正確性:
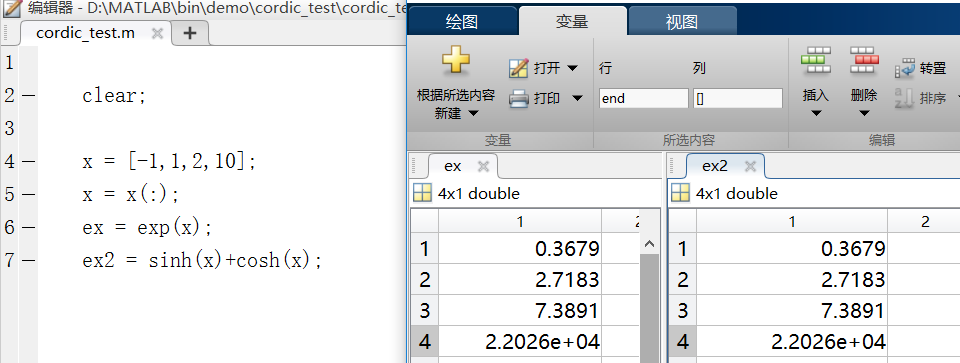
在設計后也同樣要借助MATLAB進行仿真驗證。
2. CORDIC IP核
現在通過查看user guide得知CORDIC IP核的接口及主要特性。

接口包括輸入笛卡爾數據輸入通道、相位輸入通道、全局信號以及數據輸出通道。該IP核有兩種結構:串行和并行,可根據數據吞吐量需求選擇,并行結構可以每個時鐘輸出一個計算結果。如果計算sinh和cosh,要向phase通道輸入相位信息,X_OUT是cosh(phase),Y_OUT是sinh(phase).輸入phase必須滿足數據范圍,否則出現不可預計結果。輸出幀結構及數據范圍如下:
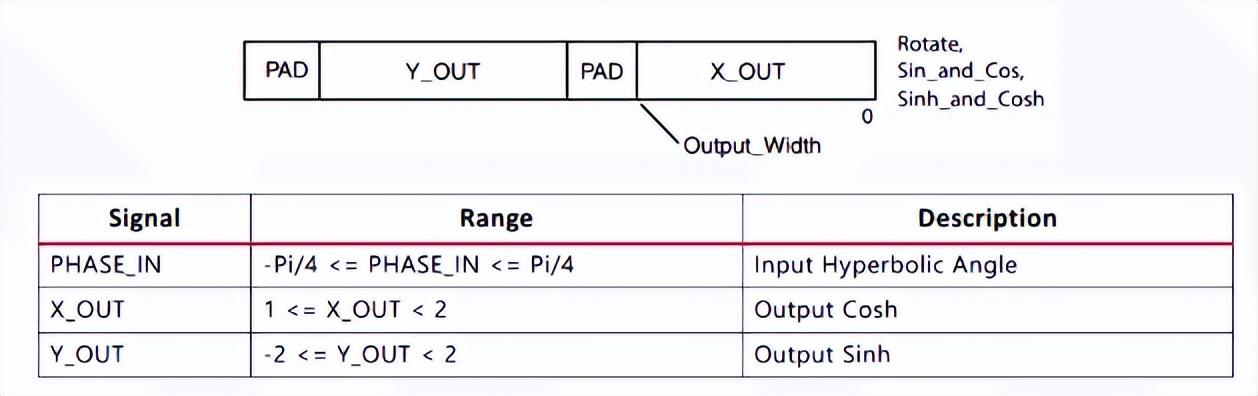
其中輸入數據格式為2QN,輸出則是1QN。由于均是有符號數,也就是輸入整數部分3bit,輸出整數部分2bit。接下來對IP核進行配置,重點是第一頁,此處將其配置為計算sinh和cosh模式,采用并行優化的流水線結構。相位以角度為單位,輸入輸出位寬設置成16bit。

3.HDL代碼設計及仿真驗證
設計代碼:
`timescale 1ns / 1ps
module cordic_ex#(parameter DIN_W = 16,
DOUT_W = 16)
(
input clk,
input [DIN_W-1:0] din,//2Q13
input din_vld,
output reg [DOUT_W+1-1:0] dout = 0,//2Q14
output reg dout_vld = 0
);
wire [DOUT_W*2-1 : 0] m_axis_dout_tdata;
wire m_axis_dout_tvalid;
wire signed [DOUT_W-1:0] sinh,cosh;
// ex = sinhx + coshx <1Q14+1Q14 = 2Q14>
always @(posedge clk)begin
dout <= sinh + cosh;
end
assign sinh = m_axis_dout_tdata[DOUT_W*2-1 -:DOUT_W];
assign cosh = m_axis_dout_tdata[DOUT_W-1 -:DOUT_W];
always @(posedge clk)begin
if(m_axis_dout_tvalid)begin
dout_vld <= 1'b1;
end
else
dout_vld <= 0;
end
cordic_0 cordic_cosh_sinh (
.aclk(clk), // input wire aclk
.s_axis_phase_tvalid(din_vld), // input wire s_axis_phase_tvalid
.s_axis_phase_tdata(din), // input wire [15 : 0] s_axis_phase_tdata
.m_axis_dout_tvalid(m_axis_dout_tvalid), // output wire m_axis_dout_tvalid
.m_axis_dout_tdata(m_axis_dout_tdata) // output wire [31 : 0] m_axis_dout_tdata
);
endmodule
cordic_ex
用MATLAB產生兩組數據,并將角度值定點化后作為設計模塊數據激勵:
testbench:
`timescale 1ns / 1ps
module cordic_ex_tb();
parameter CYC = 20;
reg clk;
reg [16-1:0] din;
reg din_vld;
wire signed [17-1:0] dout;
wire dout_vld;
cordic_ex#(.DIN_W(16),
.DOUT_W(16))
uut(
.clk (clk) ,
.din (din) ,//2Q13
.din_vld (din_vld) ,
.dout (dout) ,//2Q14
.dout_vld (dout_vld)
);
initial begin
clk = 1;
forever #(CYC/2) clk = ~clk;
end
initial begin
#1;
din = 0;
din_vld = 0;
#(CYC*10);
din_vld = 1;
din = 16'b0001010000011011;//pi * 1/5
#(CYC*1);
din = 16'b1110011011011110;//-pi * 1/4
#5;
$stop;
end
endmodule
cordic_ex_tb
仿真結果:
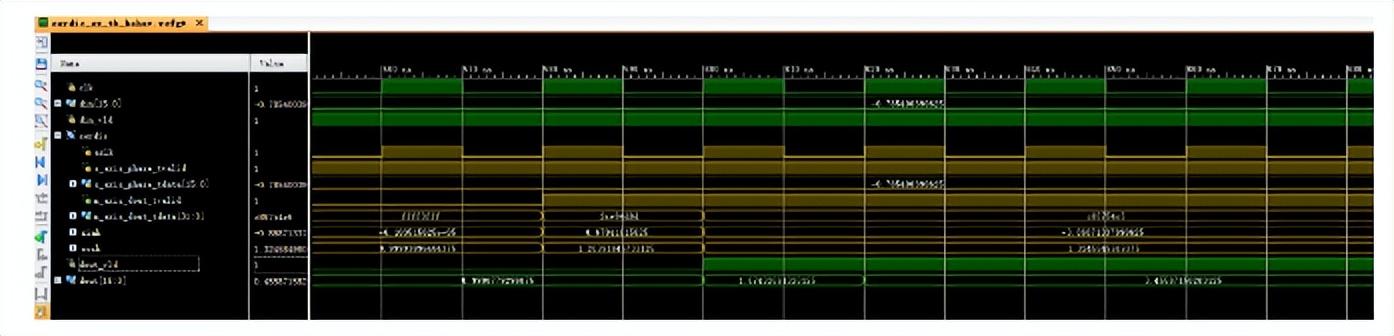
仿真波形表明,計算結果與MATLAB浮點運算相近,滿足一般計算需求。若想提高精度,可以增加CORDIC輸出數據位寬。















評論