準確測算電壓電流的雙測法
萬用電表因制作工藝所限,總會有誤差。電壓擋的量程越大內阻就越大,對被測電壓的影響就越小。但是量程越大,表指針偏轉就越小,相對誤差就隨之增大,對大內阻電源(其內阻與電壓擋內阻在一個數量級上)來說尤其如此。同樣,電流擋的量程越大,內阻就越小,對被測電流的影響就越小。但是量程越大,表指針偏轉就越小,相對誤差就隨之增大,對小內阻電源(其內阻與電流擋內阻在一個數量級上)來說尤其如此。這種矛盾現象似乎難以解決,但是只要用兩個相鄰擋,測出兩個量,再通過簡單的計算,就能獲得準確結果。
本文引用地址:http://www.104case.com/article/202204/433017.htm1 準確測算負載端電壓U和電源的電動勢E及其內阻 r
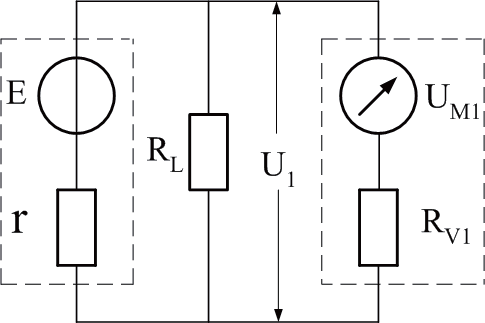
準確測算負載端電壓U 和電源的電動勢E 及其內阻r 的基本方法參見圖1(a),(b),已知:UM1(第一個電壓擋量程),U1 (第一個電壓擋測量的電壓),UM2(第二個電壓擋量程), U2(第二個電壓擋測量的電壓),RL(負載電阻),Sv(電壓擋的電壓靈敏度)。RV1 , RV2(分別是第一,第二電壓擋的內阻) E ,r(分別是電源的電動勢和內阻)。公式推導思路如下所述。
將負載和電源等效為一個帶內阻的電源,其電動勢為E0 (即為負載RL上的端電壓U)和內阻r0(r與RL并聯)。測算出E0與r0之后,則U=E0 ,又當已知RL時,即可求出r 。
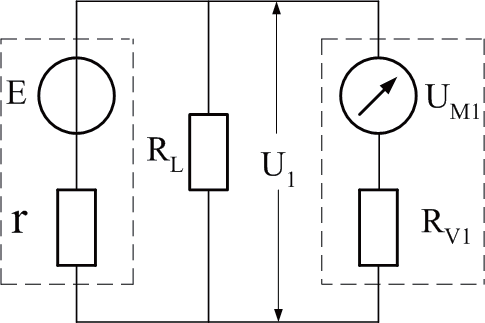
(a)
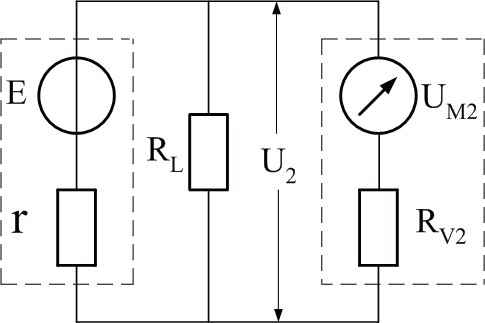
(b)
圖1 負載端電壓U1和U2測算
由圖1(a)得:

由圖1(b)得:

其中,![]()
式(1),(2)聯立,消去r0 ,得到等效電源電動勢:

式(1),(2)聯立,消去E0,得到等效電源內阻:

實際電壓:
U = E0 (5)
因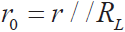 ,則電源內阻為:
,則電源內阻為:

回路電流等于負載電流,即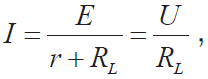 則電源電動勢為:
則電源電動勢為:

測取電壓U1和U2的相對誤差分別為:

當![]() 除去RL ,即空載時,
除去RL ,即空載時,

測取電壓U1和U2的相對誤差分別為:

(1)測算空載時的電源電動勢E 及其內阻r
已知:![]()
![]()
求:E,r,U,γ V1,γV2。
解:將已知代入式(5)、(6)、(7)、(10)、
(11)求得。下面用MTLAB 語言編程計算,見程序1。
程序1
a=input(‘a=’);Um1=input(‘Um1=’);U1=input(‘U1=’);Um2=input(‘Um2=’);U2=input(‘U2=’);Sv=input(‘Sv=’);
Rv1=Sv*Um1;Rv2=Sv*Um2;
E0=U1*U2*(Rv2-Rv1)/(U1*Rv2-U2*Rv1);
r0=Rv1*Rv2*(U2-U1)/(U1*Rv2-U2*Rv1);
if a==0 % 計算無負載時的電源電動勢E 及其內阻r
E=E0
r=r0
Gmv1=(U1-E)/E % 測量值U1 的誤差
Gmv2=(U2-E)/E % 測量值U2 的誤差
else % 計算負載端電壓U 和電源電動勢E 及其內阻r
RL=input(‘RL=’);
U=E0
r=RL*r0/(RL-r0)
E=(RL+r)*U/RL
Gmv1=(U1-U)/U % 測量值U1 的誤差
Gmv2=(U2-U)/U % 測量值U2 的誤差
End
輸入數據:
a=0
Um1=10
U1=8.57
Um2=50
U2=20
Sv=20
計算結果:
E=30.0044
r=500.2188
Gmv1=-0.7144
Gmv2=-0.3334
結果是E = 30V,r = 500 kΩ,γ V1 = ?71.44% ,γV2 ?33.34% 。
可見,測量的電壓U1 低于實際電動勢E71.44% ,顯然是不可采信的。真實的空載電動勢是30V 。
(2)測算有負載時的負載端電壓U 和電源電動勢E 及其內阻r
輸入數據:
a=1
Um1=10
U1=7.5
Um2=50
U2=15
Sv=20
RL=1000
計算結果:
U=20
r=500.0000
E=30
Gmv1=-0.6250
Gmv2=-0.2500
結果是 E = 30V , R = 500 kΩ , U = 20V ,γV1=?62.5% ,γ V 2 = ?25% 。
可見,測量的電壓U1 低于實際電壓U62.5% ,顯然是不可采信的。真實的負載端電壓是20V 。
2 準確測算負載電流I和電源電動勢E及其內阻r[1]
已知:使用萬用電表電流擋量程IM1 測得電流I1 ;另一電流擋量程IM 2 和測得電壓I2 ;萬用電表電流擋的電壓降UI 。
求:負載電流I ,電源電動勢E 及其內阻r 。
解:公式推導
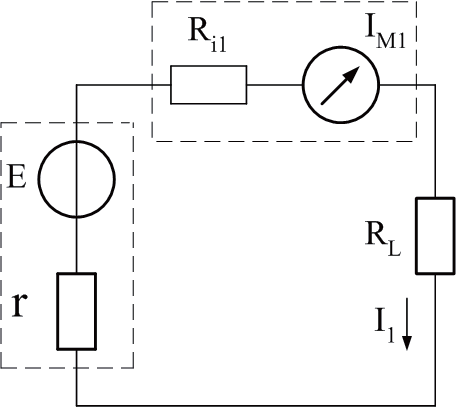
(a)
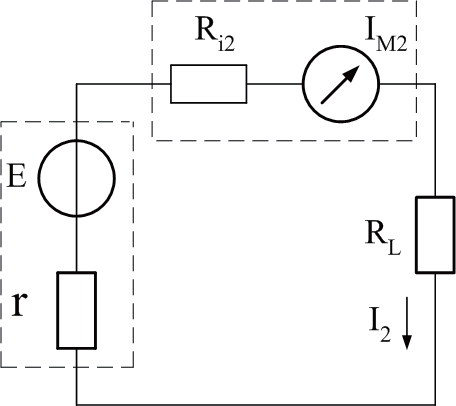
(b)
圖2
由圖2(a)得到測量電流:

由圖2(b)得到測量電流:

其中,![]() 分別為電流擋IM1, IM2的內阻。UI 是電流擋的滿量程端電壓降。
分別為電流擋IM1, IM2的內阻。UI 是電流擋的滿量程端電壓降。
式(14)和式(15)聯立,消去r ,得到電源電動勢:

式(14)和式(15)聯立,消去E ,得到電源內阻:
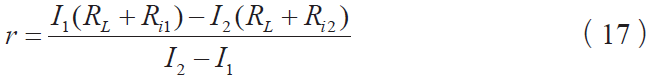
實際電流:
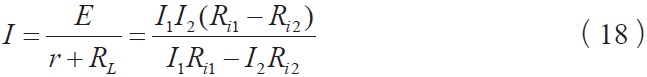
測取電流I1和I2的相對誤差:

例2 已知:![]()
![]()
Gmi2=(I2-I)/I
輸入數據:
Im1=1
I1=1
Im2=5
I2=1.154
RL=4
UI=1
計算結果:
E=5.9948
r=0.9948
I=1.2002
Gmi1=-0.1668
Gmi2=-0.0385
結果是E = 6V,r =1Ω,I =1.2 A,γ I1 = ?16.68%,γI2=?3.85%
可見,測量的電流I1 低于實際電流I16.68% ,顯然是不可采信的。真實的負載電流是1.2 A 。
3 討論
(1)在第1 項中
(a)由式(6)、式(1)和式(2)知。r = 0 時![]() 可知,電源內阻越小,則其
可知,電源內阻越小,則其
壓降就越小,測量值就越接近實際值。對市電來說,電源內阻遠遠小于電壓表內阻。測量的電壓是準確的。一般來說,對萬用電表的電壓靈敏度要求不高,不過對于經過小型電源變壓器降壓之后,電源內阻就不能忽視了。
(b)由式(1)和式(2)知,當RV1 → ∞ 時,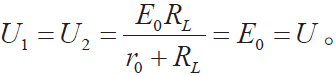 故RV1 越大,測量值就越接
故RV1 越大,測量值就越接
近于實際值。
(2)在第2 項中
當![]() 時, 由式(14) 和式(15) 變為
時, 由式(14) 和式(15) 變為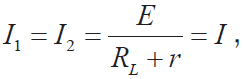
可見,電流檔內阻或電壓降越小,測量電流就更接近于實際電流。
4 結語
從上述分析和討論可知,若電源內阻為零,或電壓擋的內阻無窮大和電流檔的內阻無窮小,電壓就沒有對負載的分流作用,電流擋也沒有對負載的分壓作用,測量值就是實際值。遺憾的是這種理想情況是不存在的,于是雙測法才派上用場。
對于電工技術人員來說,雙測法的用途有限,只是在電源變壓器二次側的低壓場合可能用上;對于電子技術人員來說,遇到的多是低電壓小電流的弱電設備,雙測法是準確測定電壓電流的最好方法。
如何判斷是否使用雙測法?可將測得的兩個電壓進行比較,若相差無幾,則認為測量的電壓就是實際,否則就不得不用雙測法了。對于電平測量[2]和功率測量[3],也可用本文方法。將測定的電壓轉化為對應的電平值或功率值即可。
還需說明的是,文中所說電壓或電流的實際值或準確值,只對理想情況而言,事實上萬用電表本身各擋均有誤差,是儀器制作本身帶來的。
文中使用了MATLAB 算法語言編制程序,目前該算法語言很流行,也很好用。否則,要用計算器計算就很麻煩,也易出錯,用該程序就能快速獲取正確結果,以后還可反復使用。
參考文獻:
[1] 沙占友,王彥朋,睢丙東,杜之濤.萬用表速學巧用一本通[M].北京:中國電力出版社,2012:216-217.
[2] 呂炳仁.指針式萬用電表電平測量原理和誤差分析[J].北京:電子產品世界,2021(8):71-73.
[3] 呂炳仁.指針式萬用電表功率測量原理和誤差分析[J].北京:電子產品世界,2021(9):54-56.
(本文來源于《電子產品世界》雜志2022年3月期)




評論