基于BSM1的硝態氮濃度辨識建模
俞方罡,秦 斌(湖南工業大學,湖南 株洲 412000)
摘? 要:污水處理過程復雜多樣,為方便研究工作,根據基準仿真1號模型(Benchmark Simulation Modelno.1,BSM1)搭建simulink仿真模型。由于控制溶解氧和硝態氮濃度的穩定是污水處理過程的關鍵,所以針對傳統PI控制對大滯后非線性系統中硝態氮濃度控制性能低以及系統運行速度慢的問題,利用極限學習機(ELM)和支持向量機(SVM)的預測能力對硝態氮濃度進行模型辨識和比較。結果證明,在數據量較少的情況下,支持向量機(SVM)具有很高的精確度,但是在數據量較高的情況下,極限學習機同樣具有高精確度的特點并且運行速度更快。
關鍵詞:污水處理;極限學習機;支持向量機;MATLAB仿真
0 引言
在污水處理中,活性污泥是應用最為廣泛的處理方法,因此大量的研究工作都將活性污泥作為研究的對象。因為微生物存在的各種習性以及相互之間的作用,在最初的研究工作中學者們所提出的數學模型都存在結構非常復雜或是其應用受到限制的問題[1]。為了解決這些模型存在的問題,國際水協會(IWA)和歐盟科學技術合作組織(COST)兩個組織合力開發的基準仿真1號模型[2]。為方便研究控制策略對污水處理過程的影響,對該模型進行了simulink建模及仿真[3-6],雖然通過簡單的PI控制策略對此模型進行閉環仿真,但在系統為大滯后非線性的情況下,硝態氮濃度的控制效果并不理想[7-8]。隨著人工智能和機器學習的不斷發展,黃廣斌提出了極限學習機,這是一種基于單隱層前饋型神經網絡發展而來的智能算法,用于解決反向傳播算法學習效率低、參數設定繁瑣的問題[9-14]。宋劍杰、徐麗莎等人利用支持向量機解決出水COD、BOD的預測模型問題。對此,參考神經網絡對非線性系統辨識能力強、具有強大的自學習能力的特點,在小數據組和大數據組兩種情況下,采用極限學習機和支持向量機對硝態氮濃度進行模型辨識和比較[15]。
1 BSM1仿真及PI控制
基準仿真1號模型由ASM1活性污泥模型與Takács雙指數沉淀模型組成。兩種模型的搭建都遵守物料守恒定律,ASM1詳細的描述了污水中組分的來源、反應過程和去向,用于搭建整個系統中生化池的部分。值得注意的是缺氧池1的入水由三方面組成;三個好氧池從外界受氧。因此此二者的物料守恒有別于上述規則,分別為式(1)與式(2)所示:
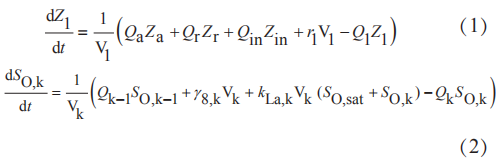
式中 Q 表示對應的流量,Z表示對應的組分,V表示對應生化池的容積,r為反應速率。但是ASM1并不能描述沉淀池的運行機理,由于BSM1中只需要考慮一維空間固相與液相的變化,因沉淀池的運行機理采用Takács雙指數沉淀模型進行描述。如式(3)所示,式 中 Xf 為組分中易沉降顆粒性物質, Vs 為沉降速率,其余動力學參數均可查詢得到。
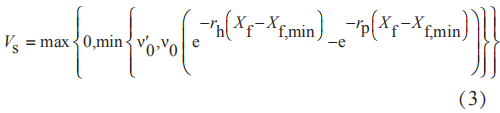
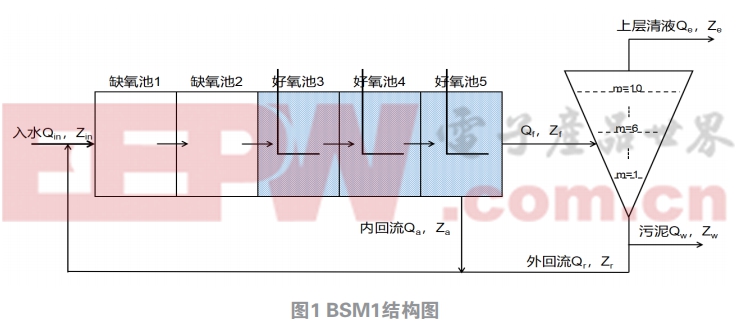
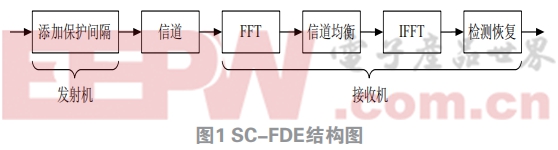
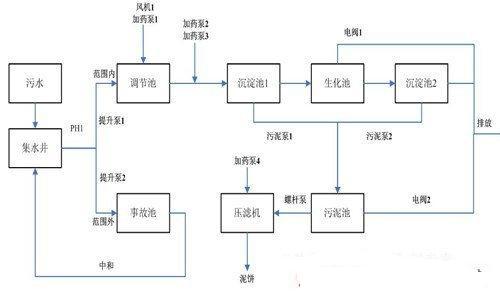
圖1為BSM1結構圖,箭頭表示污水處理過程中水流方向,按A2/O工藝流程,前兩個缺氧池容積均為1000 m3,后面三個好氧池容積均為1333 m3,最后沉淀池容積設定為6000 m3,根據ASM1與Takács模型可以在simulink中搭建模型如圖2所示。可以看出基本與BSM1結構圖是相同的,但是因為生化池的入水與出水有兩種回流液的參與,所以需要加設水流混合模塊與水流分離模塊。由于污水處理模型方程復雜,為保證simulink的運行效率,生化池與沉淀池兩個部分均采用S函數描述其內部機理。模型中所涉及的參數均查詢得到。
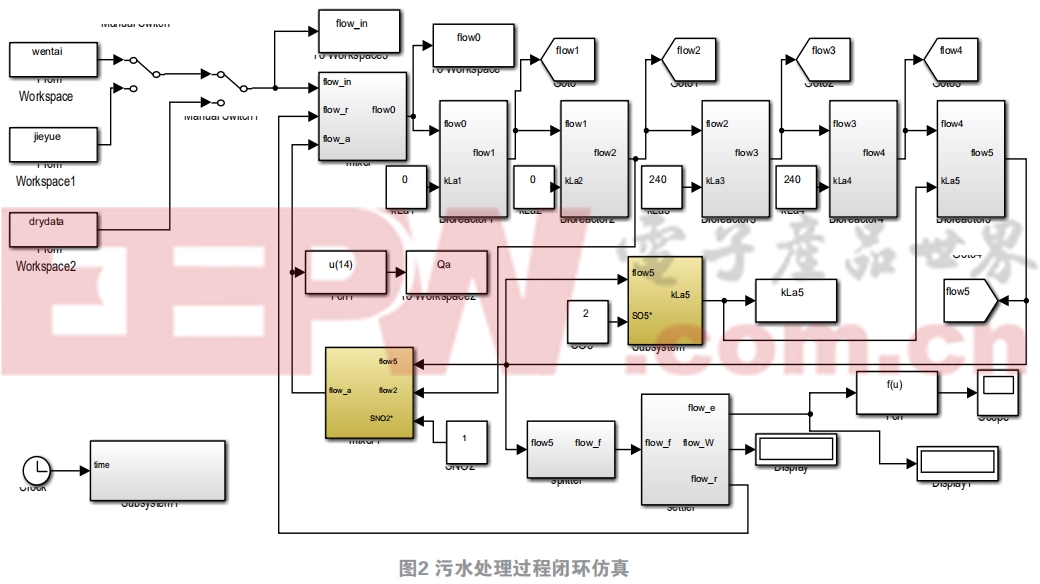
在此模型基礎上,利用傳統PI控制對模型進行閉環仿真。本文用三種不同的入水數據,即穩態入水數據、階躍入水數據和實際入水數據,選擇溶氧濃度和硝態氮濃度作為PI控制對 象 。 實際溶氧濃度一般在0.3 g/m3~7.45 g/m3之間,如此巨大的濃度波動是由于好氧池中的耗氧量在時刻變化而氧傳遞系數不變導致的,因此通過COD(COD能間接反映出池中耗氧量大小)的變化隨時調整氧轉移系數kla5來穩定溶氧濃度。同時好氧池溶解氧的濃度會影響缺氧池硝態氮濃度,在PI控制前,溶氧濃度在三種入水數據輸入的情況下,輸出曲線如圖3所示。顯然隨著耗氧量的增加,溶氧濃度在隨之減小。此時的氧傳遞系數是保持不變的,除穩態輸入外,其他入水情況均使溶氧濃度和硝態氮濃度出現較大波動,雖然穩態入水能使溶氧保持穩定,但是濃度卻沒有達到要求。圖4是硝態氮濃度的變化曲線,與溶解氧濃度相同,其波動范圍非常大。
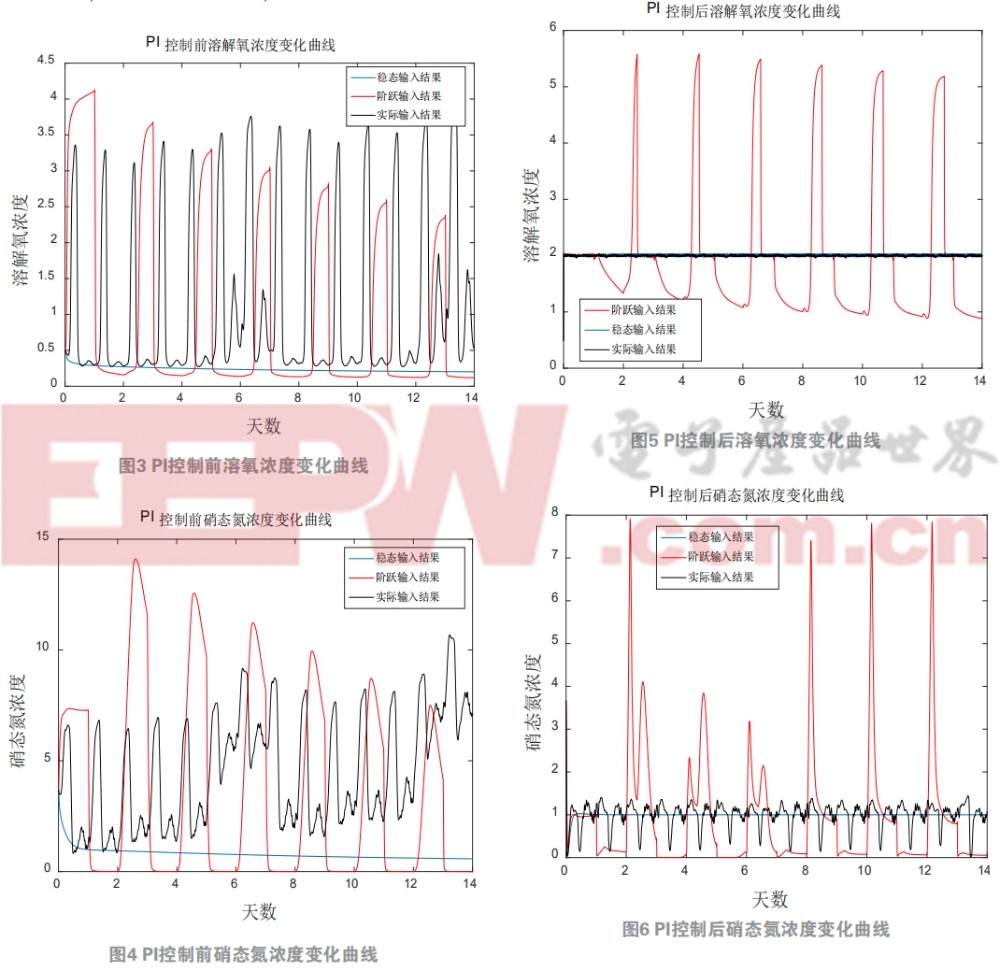
在圖2位置加入PI控制器后,仿真的結果如圖5和圖6所示。階躍輸入情況下數據每次階躍變化的幅度都很大,因此階躍輸入可以理解為多條穩態輸入數據的集合,在每一次變化時相當于系統重新進行調節,存在一定的超調量但能迅速返回設定值,在實際輸入情況下,溶氧濃度能夠控制在了2 g/m3左右。但是缺氧池出水的硝態氮濃度波動范圍依然較大,還有很大的優化空間。
2 模型辨識與結果對比
基準仿真1號模型中PI控制效果不夠強大并且運行效率低下,主要原因在于BSM1參數多,模型復雜,工業生產中神經網絡控制策略已經發揮了巨大作用,其對非線性系統的學習能力可以應用于污水處理過程控制中去,因此利用極限學習機和支持向量機建立污水處理中硝態氮濃度的簡化模型。
南洋理工大學黃廣斌教授提出極限學習機算法是由基于單隱層前饋型神經網絡發展而來的智能算法,相比于前饋神經網絡反向傳播算法學習效率低、參數設定繁瑣的問題,ELM避免了局部最優解的同時大大提高了學習速度,這在污水處理過程控制中非常重要。因為由單隱層前饋神經網絡發展而來,其結構相同可表示為式(4)
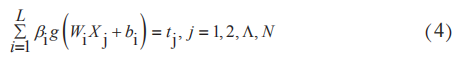
式中g(x)為激活函數;W為輸入層到隱含層的權值;β為隱含層到輸出層的權值;b為隱含層節點偏置。
這里采用sigmoid函數作為激活函數,以真實干燥天氣入水數據作為采樣數據,利用BSM1仿真模型采集2號缺氧池出水13個組分作為極限學習機的輸入變量X,5號好氧池溶解氧濃度作為極限學習機的輸出變量t,分別采集1345組作為小數據組和10000組作為大數據組,其中70%作為訓練數據,30%作為測試數據,分別用訓練數據和測試數據與實際數據進行對比。用矩陣可表示為式(5)

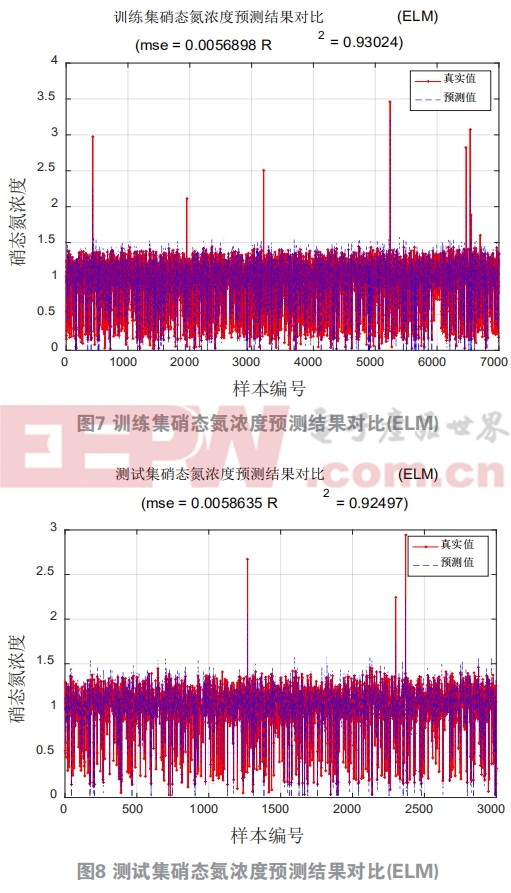
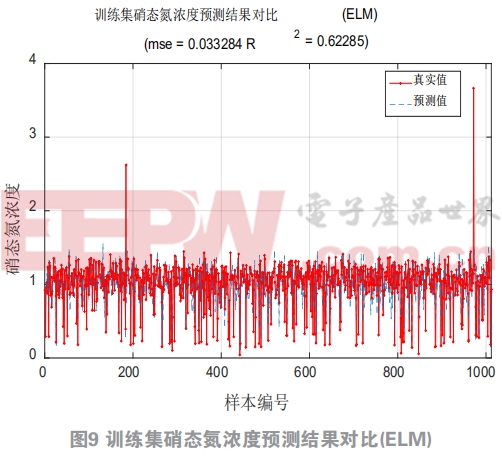
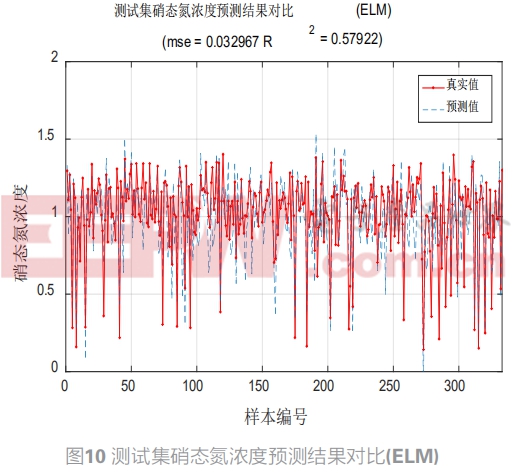
多數情況下H是不可逆矩陣,只有通過使代價函數最小化來尋找權值,由于極限學習機算法中隨機給定初始輸入權重W和節點偏置b,所以極限學習機的泛化性可以通過調節隱含層節點數L提高,同時理論指出單隱層神經網絡權重幅值越小,網絡的泛化性能就越強。這里選取節點數為300。圖7圖8為大數據組結果,圖9圖10為小數據組結果,在小數據組中,極限學習機的辨識精確度較低,但是在大數據組中極限學習機的運行速度依然很快并且具有較好的預測效果,訓練集和測試集的性能指標都達到了0.9以上。
為比較極限學習機污水處理預測模型的預測性能,建立支持向量機污水處理預測模型,支持向量機相比于普通的神經網絡,在學習復雜的非線性方程時能夠提供一種更清晰更強大的方式。由于污水處理系統非線性程度很高,樣本數量與特征量數量差距非常大,容易出現欠擬合和過擬合的問題,為了使SVM具有良好的泛化性,需要在代價函數中加入正則化風險,代價函數如式(6)所示:

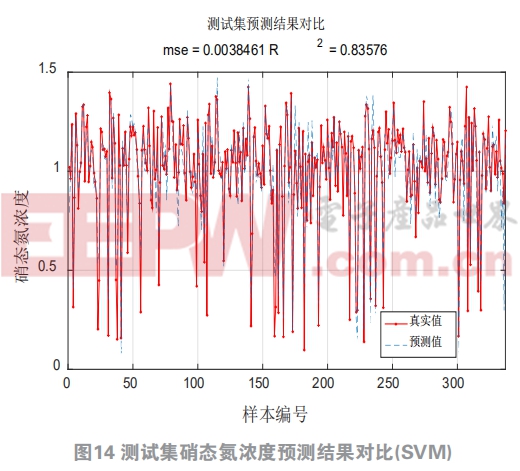
式中ei為i號樣本的誤差; 1/2ωTω為正則化風險,用真實干燥天氣入水數據作為采樣數據,對作為輸入變量的5號好氧池出水13個組分和作為輸出變量的硝態氮進行采集,同樣采樣1345組數據作為小數據組和10000組作為大數據組,其中70%作為訓練數據,30%作為測試數據,分別用訓練數據和測試數據與實際數據進行對比。圖11圖12為大數據組結果,圖13圖14為小數據組結果,小數據組中,無論是訓練集還是測試集,支持向量機的辨識精度遠高于同組的極限學習機,圖中紅色實線的真實值和藍色虛線的預測值基本保持一致,支持向量機對于內回流中的硝態氮濃度有很好的預測效果。但是在大數據組中,支持向量機的精度優勢已經不再具備,相反其運行速度卻遠低于極限學習機。

極限學習機的訓練速度遠高于支持向量機,因為極限學習機算法中直接生成初始化輸入權重和隱含層節點偏置,不需要迭代調整,而支持向量機對正則化參數和核函數參數的選取比較費時,極限學習機通過調整隱含層節點數可以調節模型的泛化性和預測精度,相比于支持向量機運用更加簡便。在數據量比較少的情況下,支持向量機的辨識精度很高,具有明顯的優勢,但是數據量較多的時候,極限學習機的精度不比支持向量機低,同時擁有更快的辨識速度,此時極限學習機要優于支持向量機。
3 結論
污水處理過程是個長時間過程,對處理系統進行基于BSM1的simulink建模提高了研究工作的效率,針對PI控制對硝態氮濃度控制能力低下的問題,建立基于ELM的簡化模型和基于SVM的簡化模型。結果表明,兩者都有不錯的大滯后非線性系統的模型辨識性能,SVM的辨識精度很高,但在數據量很大的情況下,ELM的精度也同樣很高,其建模簡單,訓練速度快的特點更具優勢。現在污水處理過程中對數據進行采集是普遍的現象,這些數據對神經網絡來說是非常重要的部分,具有不同針對性的污水處理過程是可以采用不同的神經網絡建模,無論是ELM還是SVM都為污水處理提供了非常有效的方法,溶解氧濃度和硝態氮濃度穩定是污水處理過程控制的關鍵,精確的預測模型對提高控制性能有重要作用。
參考文獻
[1] 李春陽. 基于ASM1活性污泥污水處理過程的建模與控制問題研究[D].哈爾濱:哈爾濱工業大學,2016.
[2] 王藩, 王小藝, 魏偉,等. 基于BSM1的城市污水處理優化控制方案研究[J]. 控制工程, 2015, 22(6):1224-1229.
[3] 張琪. 活性污泥法城市污水處理系統的建模與仿真[D]. 北京:北京化工大學, 2015.
[4] Gaitang H , Junfei Q , Honggui H . Wastewater treatmentcontrol method based on recurrent fuzzy neural network[J].Ciesc Journal, 2016.
[5] 喬興宏. 污水生化處理系統的智能預測及魯棒優化控制研究[D].廣州:華南理工大學,2016.
[6] 周紅桃. 焦化污泥熱解資源化與廢水處理能量當量建模及節能優化[D].廣州:華南理工大學.
[7] 王雨萌. 基于智能控制策略的污水處理控制系統[D]. 杭州:浙江大學,2018.
[8] 劉幫, 秦斌, 彭小玉. 污水出水水質的SVR建模[J]. 新型工業化,2015(1).
[9] 許玉格, 鄧文凱, 鄧曉燕, et al. 基于核函數的加權極限學習機污水處理在線故障診斷方法[J]. 化工學報.
[10]宋翼頡, 王欣. 基于LSSVM的污水處理過程預測控制[J]. 新型工業化, 2015(8):33-38.
[11]林梅金. 污水生化處理系統的智能預測及優化控制策略研究[D].廣州:華南理工大學,2015.
[12]王欣, 宋翼頡, 秦斌,等. 基于LSSVM的污水處理過程建模[J]. 湖南工業大學學報, 2016, 30(1):59-63.
[13]甘露. 極限學習機的研究與應用[D]. 西安:西安電子科技大學,2014.
[14]楊易旻. 基于極限學習的系統辨識方法及應用研究[D]. 長沙:湖南大學, 2013.
[15]秦斌, 易懷洋, 王欣. 基于極限學習機的風電機組葉根載荷辨識建模[J]. 振動與沖擊, 2018.
本文來源于科技期刊《電子產品世界》2020年第02期第49頁,歡迎您寫論文時引用,并注明出處。






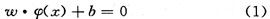
評論