用PCA還是LDA?特征抽取經典算法PK
在之前的格物匯文章中,我們介紹了特征抽取的經典算法——主成分分析(PCA),了解了PCA算法實質上是進行了一次坐標軸旋轉,盡可能讓數據映射在新坐標軸方向上的方差盡可能大,并且讓原數據與新映射的數據在距離的變化上盡可能小。方差較大的方向代表數據含有的信息量較大,建議保留。方差較小的方向代表數據含有的信息量較少,建議舍棄。今天我們就來看一下PCA的具體應用案例和特征映射的另一種方法:線性判別分析(LDA)。
本文引用地址:http://www.104case.com/article/201901/396508.htmPCA案例
在機器學習中,所使用的數據往往維數很大,我們需要使用降維的方法來突顯信息含量較大的數據,PCA就是一個很好的降維方法。下面我們來看一個具體的應用案例,為了簡單起見,我們使用一個較小的數據集來展示:
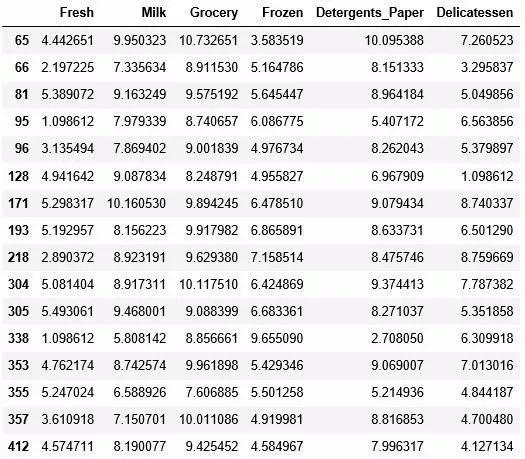
顯而易見,我們數據有6維,維數雖然不是很多但不一定代表數據不可以降維。我們使用sklearn中的PCA算法擬合數據集得到如下的結果:
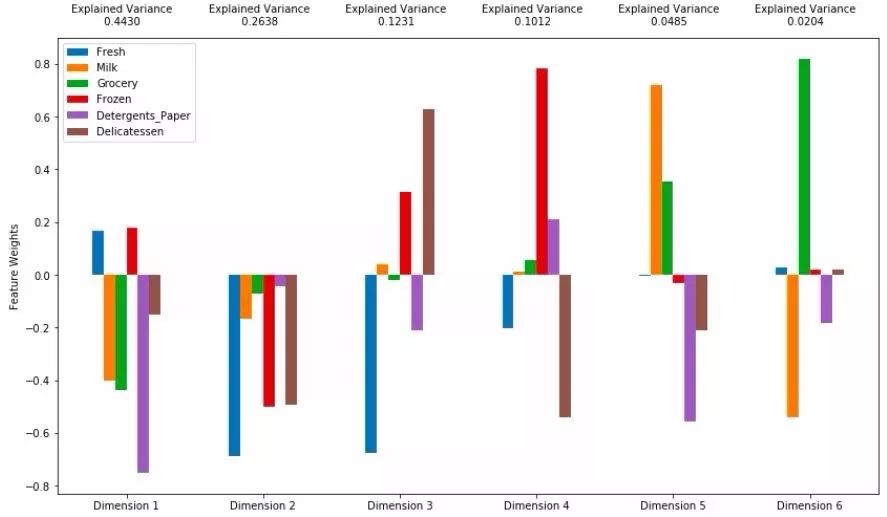
我們可以看到經過PCA降維后依然生成了新的6個維度,但是數據映射在每一個維度上的方差大小不一樣。我們會對每一個維度上的方差進行歸一化,每一個維度上的方差量我們稱為可解釋的方差量(Explained Variance)。由圖可知,每一個維度上可解釋方差占比為:0.4430,0.2638,0.1231,0.1012,0.0485,0.0204。根據經驗來說我們期望可解釋的方差量累計值在80%以上較好,因此我們可以選擇降維降到3維(82.99%)或者4維(93.11%),括號中的數字為累計可解釋的方差量,最后兩維方差解釋只有7%不到,建議舍去。圖中的柱狀圖表示原維度在新坐標軸上的映射向量大小。在前兩維度上表現如下圖所示:

PCA雖然能實現很好的降維效果,但是它卻是一種無監督的方法。實際上我們更加希望對于有類別標簽的數據(有監督),也能實現降維,并且降維后能更好的區分每一個類。此時,特征抽取的另一種經典算法——線性判別分析(LDA)就閃亮登場了。
LDA簡介
LDA是一種監督學習的降維技術,也就是說它的數據集的每個樣本是有類別輸出的。這點和PCA不同。PCA是不考慮樣本類別輸出的無監督降維技術。LDA的思想可以用一句話概括,就是“投影后類內方差最小,類間方差最大”。什么意思呢? 我們要將數據在低維度上進行投影,投影后希望每一種類別數據的投影點盡可能的接近,而不同類別的數據的類別中心之間的距離盡可能的大。
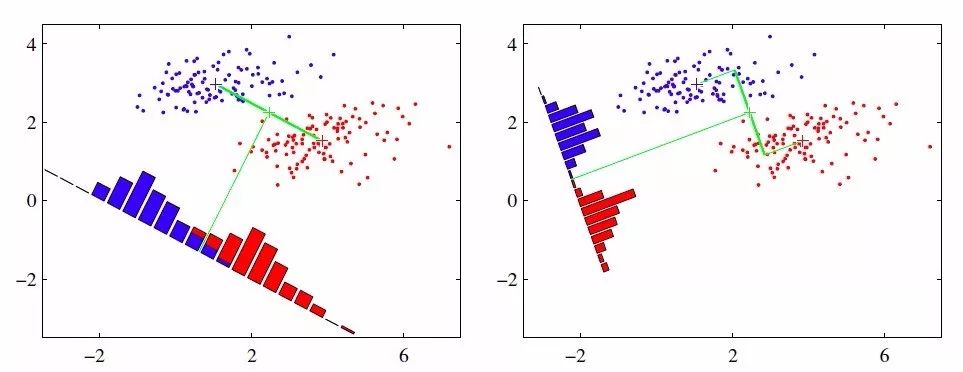
上圖中提供了兩種投影方式,哪一種能更好的滿足我們的標準呢?從直觀上可以看出,右圖要比左圖的投影效果好,因為右圖的黑色數據和藍色數據各個較為集中,且類別之間的距離明顯。左圖則在邊界處數據混雜。LDA的降維效果更像右圖,它能在新坐標軸上優先區分出兩個類別,它是如何實現的呢?
LDA的原理
LDA的主要思想是“投影后類內方差最小,類間方差最大”。實質上就是很好的區分出兩個類的分布。我們知道衡量數據分布的兩個重要指標是均值和方差,對于每一個類,他們的定義如下:
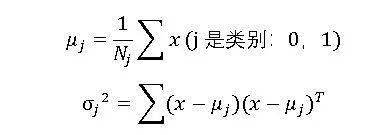
與PCA一樣,LDA也是對數據的坐標軸進行一次旋轉,假設旋轉的轉移矩陣是w,那么新的旋轉數據可以表示為:
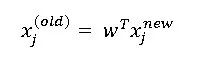
同理,兩個類別的中心點也轉換成了:
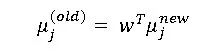

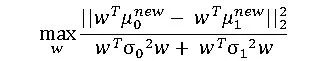
我們求解這個最優化問題,即可求出轉移變換矩陣w,即LDA的最終結果。
PCA vs LDA
LDA用于降維,和PCA有很多相同,也有很多不同的地方,因此值得好好的比較一下兩者的降維異同點。首先我們看看相同點:
1、兩者均可以對數據進行降維
2、兩者在降維時均使用了矩陣特征分解的思想
3、兩者都假設數據符合高斯分布
我們接著看看不同點:
1、LDA是有監督的降維方法,而PCA是無監督的降維方法
2、LDA降維最多降到類別數k-1的維數,而PCA沒有這個限制
3、LDA除了可以用于降維,還可以用于分類
4、LDA選擇分類性能最好的投影方向,而PCA選擇樣本點投影具有最大方差的方向
在某些數據分布下LDA比PCA降維較優(左圖),在某些數據分布下,PCA比LDA降維較優。
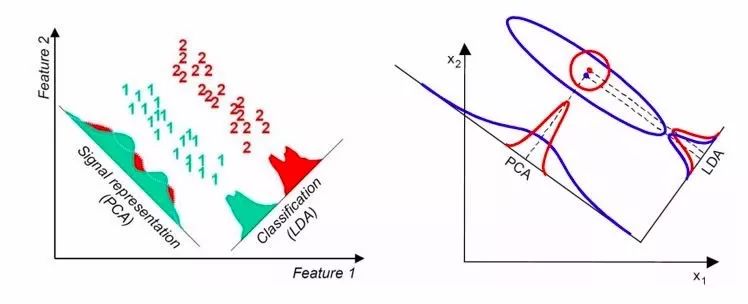
好了,以上就是本期格物匯的內容,我們下期見。




評論