利用Multisim實現(xiàn)SAR-ADC的原理仿真與設(shè)計
作者 張彪 莘濟豪 梁文哲 北京理工大學(xué)(北京100081)
本文引用地址:http://www.104case.com/article/201812/396104.htm摘要:本文介紹了基于Multisim的SAR-ADC原理仿真與設(shè)計,利用模塊化的方式分析了SAR-ADC時鐘控制、切變電路、電容陣列的工作原理及設(shè)計,同時利用橋接電容減少了電容陣列的面積,列出了部分ADC的性能指標以及計算方法,并且利用wavevison測量出此ADC的性能。
關(guān)鍵詞:SAR-ADC;電容陣列;切變電路;單轉(zhuǎn)差模塊
張彪,1996年生,男,本科生,主要從事信號處理方向的學(xué)習(xí)與研究;莘濟豪,1997年生,男,本科生,主要從事信號處理方向的學(xué)習(xí)與研究;梁文哲,1996年生,男,本科生,主要從事信號處理方向的學(xué)習(xí)與研究。
1 SAR-ADC工作原理
逐次逼近轉(zhuǎn)換器(SAR-ADC)由采樣保持、比較器、DAC和數(shù)字控制邏輯組成,其工作原理圖如圖1所示。而數(shù)字控制邏輯由逐次逼近寄存器(SAR)和控制邏輯組成。其具體工作過程如下:
●模擬輸入先經(jīng)過采樣保持送到比較器的一端,轉(zhuǎn)換開始時,數(shù)字控制邏輯將逐次逼近寄存器(SAR)的最高位(MSB)置為1,其余位為0。
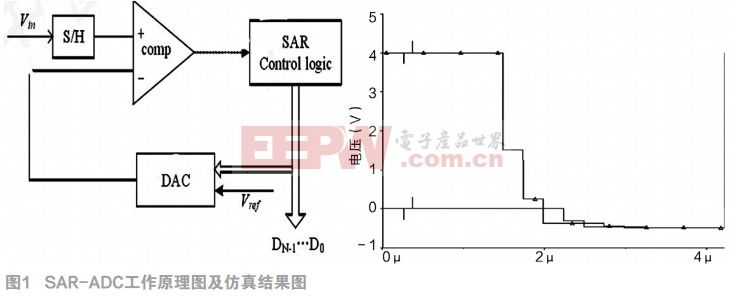
●DAC在SAR和控制邏輯的控制下,將Vin<Vref,送入到比較器的另一端, 此時Vin和1/2Vref進行,如果Vin>1/2Vref,比較器輸出1,則SAR最高位為1,如果Vin<1/2Vref,比較器輸出0,SAR最高位輸出0。
●以此類推確定到SAR的最低位,完成N位數(shù)字碼的確定,此時得到的數(shù)字量即為模擬輸入的二進制代碼。
2 12bitSAR-ADC的設(shè)計與仿真
2.1原理設(shè)計說明
該設(shè)計的12bitADC具有低功耗和高精度的特點。它的原理圖如圖2。全差分的輸入信號經(jīng)采樣開關(guān)和電荷定標型DAC陣列后,輸入到比較器的兩端。比較器的結(jié)果輸入到SAR控制邏輯(即DAC電平切變電路),SAR控制邏輯可以根據(jù)比較器的結(jié)果來控制電容DAC陣列的電平切換開關(guān),使DAC陣列的電荷重新分派。因此比較器的輸入發(fā)生變化,然后在下一個時鐘的低電平進行比較,并繼續(xù)將比較結(jié)果送入SAR控制邏輯,之后不斷重復(fù)。在12個比較周期后,可由SAR的輸出得到12位數(shù)字結(jié)果。此時系統(tǒng)復(fù)位,等待下一次比較。
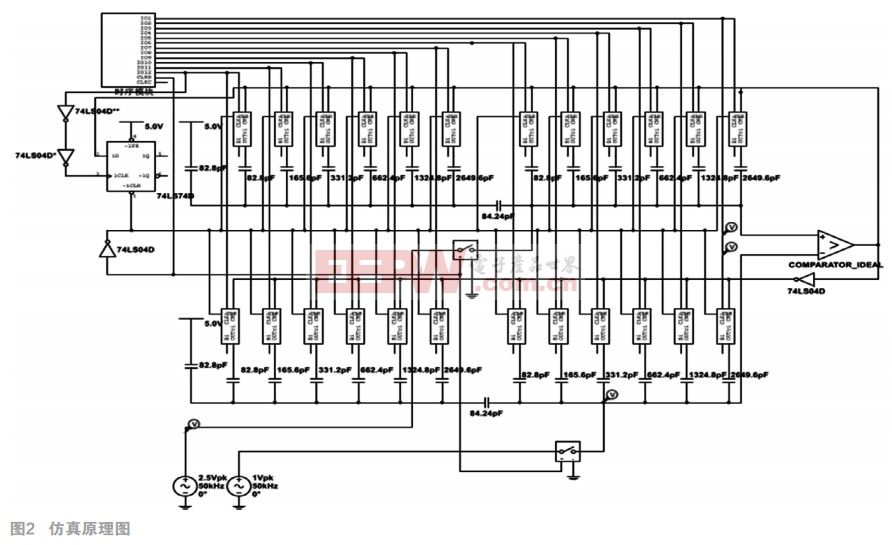
電路圖左上角是時序產(chǎn)生電路,由此為ADC提供采樣時鐘,比較時鐘;中間部分是SAR控制邏輯(即DAC電平切變電路)和電容DAC陣列;最右邊是理想比較器;左下方是差分輸入的正弦信號。
由圖中可見,差分輸入的正弦信號經(jīng)采樣開關(guān)輸入到電容DAC陣列中和理想比較器的兩端。之后比較器的輸出輸入到SAR控制邏輯從而控制DAC陣列的電平切換,使比較器的輸入發(fā)生變化。而數(shù)字結(jié)果可由SAR控制邏輯輸出。
SAR ADC電路的缺點是轉(zhuǎn)換位數(shù)較高時,精度容易不足。因此針對12bit的ADC,我們對時序產(chǎn)生電路和SAR DAC模塊電路部分進行了創(chuàng)新型設(shè)計,從而來提高ADC的轉(zhuǎn)換精度,具體的設(shè)計細節(jié)將在下面的各電路模塊設(shè)計予以介紹。
2.2各模塊設(shè)計說明
2.2.1控制時鐘產(chǎn)生電路
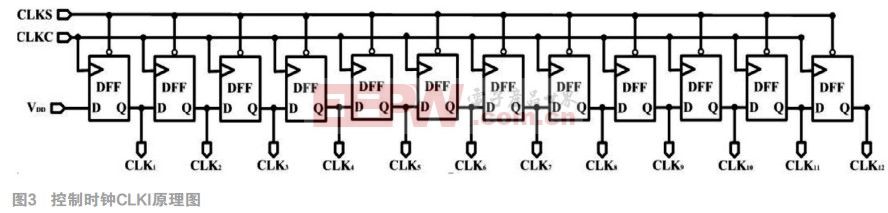
如圖3所示,控制時鐘產(chǎn)生電路由采樣時鐘CLKS和比較時鐘CLKC以及12位移位寄存器級聯(lián)而成。CLKI的產(chǎn)生原理為:
●當(dāng)CLKS為1時,CLKC、各CLKi信號均置0,此時系統(tǒng)工作在采樣/保持階段;
●CLKS為0時,此時系統(tǒng)工作在比較階段,產(chǎn)生12周期CLKC信號,并由CLKC控制移位寄存器的信號傳遞(上升沿觸發(fā)),從而產(chǎn)生CLK1-CLK12的控制時鐘。
2.2.2DAC電平切變控制電路
DAC電平切變控制電路主要功能是根據(jù)比較器的輸出結(jié)果來控制電容陣列的電平變換。為了更好的實現(xiàn)差值電平的折半比較,本設(shè)計采用圖4所示的電路結(jié)構(gòu)。
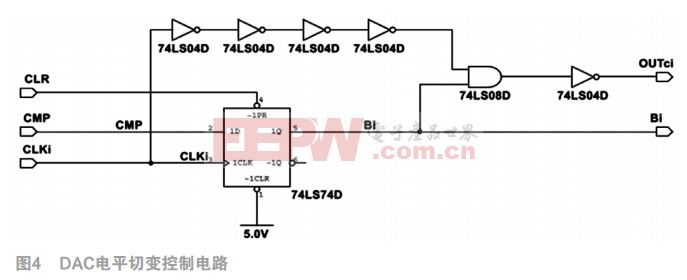
2.2.3電容陣列
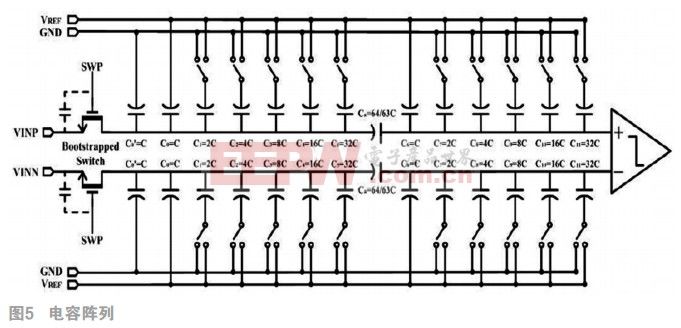
為了實現(xiàn)逐次逼近ADC的低功耗DAC,我們選用了電荷定標型結(jié)構(gòu),同時采用并行二進制加權(quán)電容陣結(jié)構(gòu)。考慮到本設(shè)計所做的是12bitADC,那么12位DAC就需要4096個單位電容,會占用較大芯片面積同時導(dǎo)致轉(zhuǎn)換速度降低。為了解決上述問題,DAC采用分段電容陣列結(jié)構(gòu)。如圖5所示,考慮到橋接電容兩端的二進制加權(quán)電容陣列位數(shù)相等時,整個逐次逼近的ADC總電容最小。因此在高6位與低6位之間用一個橋接電容Cs分隔,同時低四位二進制加權(quán)電容陣列還會接一個與單位電容等值的C。采用該種設(shè)計可以將電容的數(shù)量從4096減少到約128個。因此ADC的速度更快,功耗更小,芯片面積也更小。關(guān)于單位電容C的選取,本設(shè)計綜合考慮減小功耗和抑制噪聲的影響,選擇單位電容的容值為82.8pf。橋接電容Cs
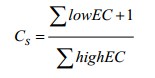
計算可得Cs=84.11pf。綜合考慮到AD轉(zhuǎn)換的精確度和累計誤差,橋接電容的容值為84.24pf。
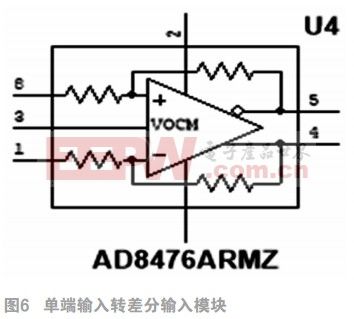
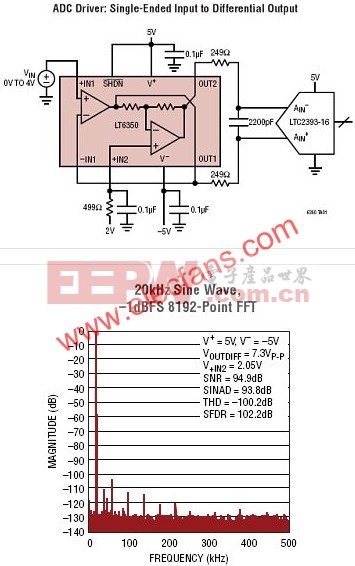
2.2.4單端輸入轉(zhuǎn)差分輸入模塊
考慮到所設(shè)計的ADC是差分輸入,而一般信號都單端輸入形式。因此在電路中附加了單端輸入轉(zhuǎn)差分輸入模塊AD8476,以保證差分信號同相以及充分抑制共模信號,如圖6。
2.2.5 12bitADC電路設(shè)計創(chuàng)新點
(1)采用邏輯門與觸發(fā)器的方式產(chǎn)生時鐘信號,靜態(tài)功耗極低,動態(tài)功耗較小。
(2)電容陣列采用分段電容,加入了橋接電容,大大減小了電容面積,提高了ADC的速快,降低了功耗。
3ADC測試指標介紹
3.1靜態(tài)指標
分辨率
分辨率是指ADC能夠分辨量化的最小信號的能力。如12位bit的ADC的分辨率為Vref/4096。
失調(diào)誤差
定義為輸入信號為零時輸出信號不為零的值,失調(diào)誤差會使實際的傳遞函數(shù)與理想傳遞函數(shù)間存在一個固定的偏移。
微分非線性
微分非線性(differentialnonlinearity,簡稱DNL)指在消除失調(diào)誤差和增益誤差后,實際轉(zhuǎn)移的臺階電壓與理想臺階電壓(LSB)之差。其計算公式如下。其中,V實際碼寬為實際測量1LSB對應(yīng)的電壓寬度;V理想碼寬為理想的1LSB電壓寬度。
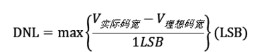
其中, V實際碼寬為實際測量1LSB對應(yīng)的電壓寬度; V理想碼寬為理想的1LSB電壓寬度。
積分非線性
積分非線性(Integratednonlinearity,INL)指在消除失調(diào)和增益誤差之后,實際傳輸函數(shù)偏離理想中心線的程度。其計算公式如下。
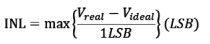
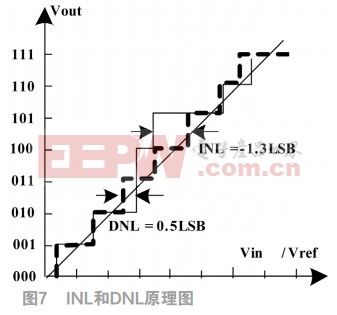
其中Vreal為實際測量的臺階電壓值;Videal為理想的臺階電壓值。INL和DNL的原理如圖7所示。
3.2動態(tài)指標
信噪比
信噪比(Signal—to—NoiseRatio,縮寫為SNR)指的是ADC滿量程單頻的正弦波輸入信號功率與ADC輸出信號在奈奎斯特帶寬內(nèi)的全部其它頻率分量(不包括直流和諧波分量)的總功率之比。理論上,ADC的信噪比取決于系統(tǒng)的位數(shù)。
其理論計算公示如下。
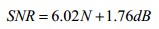
實際測量時,其計算公式如下。
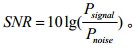
信號噪聲失真比
信號噪聲失真比也稱為信納比,可簡寫為SNDR,指的是ADC滿量程單頻的正弦波輸入信號功率與ADC輸出信號在奈奎斯特帶寬內(nèi)的全部其它頻率分量(包括噪聲和所有諧波分量)的總功率之比,通常用dB表示。其計算公式如下。
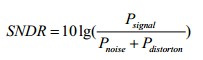
有效位數(shù)
對于一個非理想ADC,因為輸出中量化噪聲和失真引起的高次諧波的存在,實際的轉(zhuǎn)換位數(shù)小于N。因此ADC實際的轉(zhuǎn)換位數(shù)稱之為有效為數(shù),其可由測量出的信納比算出。其計算公式如下。
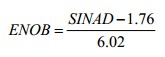
無雜散動態(tài)范圍
無雜散動態(tài)范圍是指ADC輸出頻譜中信號功率(Ps)與最大諧波分量功率(Pworst)的比值。其計算公式如下。
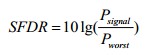
總諧波失真
一般縮寫為THD,定義為系統(tǒng)所有諧波的總功率與輸入信號功率之比。它可提供系統(tǒng)對稱和非對稱非線性產(chǎn)生的總失真大小,用以表達其對信號的諧波含量的作用或者影響。其計算公式如下。
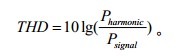
實際測量時,常用碼密度法來測量DNL和INL,用FFT分析法來測量動態(tài)指標。
4電路測試結(jié)果
輸入正弦波
差分輸入,分別輸入幅度為2.5V,電壓偏移為2.5V,頻率為22Khz的正弦波和幅度為1.5V,電壓偏移為2.5V,頻率為22kHz的正弦波。
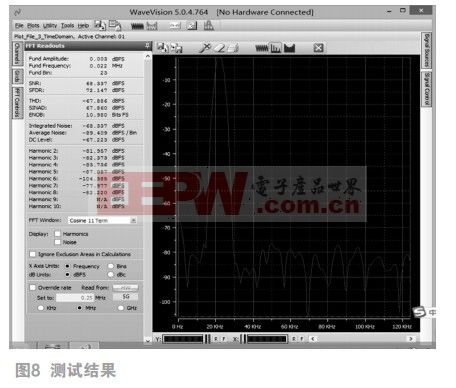
基于wavevision測試結(jié)果從圖8中可讀得:
信噪比(SNR)=68.887dBFS;
最大雜散動態(tài)(SFDR)=72.147dBFS;
總諧波失真(THD)=-66.886dBFS;
信納比(SINAD)=67.860Dbfs;
有效位數(shù)(ENOB)=10.980bits。
參考文獻:
[1]Y.Zhu et al.A 10-bit 100-MS/s reference-free SAR-ADC in90nmCMOS[J].IEEEJ.solidstateCircuits,vol.45,no.6,pp.111-1121,jun.2010
[2]R.J.Baker,cmos circuitdesign,layout,and simulation,2nd ed[m].new york:wiley,2004
[3]歐陽文偉.ADC和DAC工作原理比較和發(fā)展現(xiàn)狀.湖北教育學(xué)院學(xué)報.2005(3):22-2
[4]孫彤。低功耗逐次逼近模數(shù)轉(zhuǎn)換器的研究與設(shè)計[學(xué)位論文].清華大學(xué).2007.20-23
[5]郝樂.基于低電壓高精度 12-bit SAR ADC設(shè)計[學(xué)位論文].北京交通大學(xué).2008.17-25
本文來源于中國科技期刊《電子產(chǎn)品世界》2019年第1期第62頁,歡迎您寫論文時引用,并注明出處









評論