基于復雜網絡理論的電力網絡線路脆弱性分析

       3電力網絡線路脆弱性

　　3.1電力系統潮流算法

　　電網功率的大小取決于傳輸線參數和節點電壓。為了達到簡化方法的目的，假設電網線路是無損耗的，電網功率將取決于節點電壓和線路電抗。在這個假設無損電網的環境下，vi，vj是電壓，αij是電壓之間的相位角，xij是線路之間的電抗，則節點i到節點j的有功功率P為：

　　從公式4可看出，從任一節點i傳輸到節點j的傳輸線的功率與該線的電抗成反比，即。此處的簡化算法，沒有考慮線路兩端節點的相角和電壓。

　　3.2介數指標

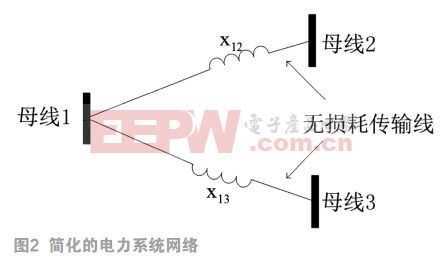
　　基于前一節的假設，可得傳輸網絡中任何線路的功率量與其電抗成反比。因此，我們將連接傳輸線的電抗定義為連接線的權重。圖2的π型等效電路表示了具有三個節點與兩條無損傳輸線的網絡。線路的電抗分別是x12和x13。如果x12<x13， 從線路1流到線路2會比從線路1到線路3有更大的功率。 因此， 若是路徑能符合權重較小的特點， 則它將能高效傳播， 傳播路徑的有效功率也會更大。 線路在電力系統中傳輸功率的大小取決于其在網絡中的位置及其在當前線路中的電抗值。 這個電抗值可以作為介數指標來確定電力系統網絡的線路的脆弱性。 高介數指標作為識別線路的關鍵。 因此， 線路的電抗及其位置有助于識別易受攻擊的線路。

　　3.3最短路徑

　　令G=(V，E)是一個網絡，其中V={1,2,3，…，n}是頂點，E是節點之間的鏈接且被賦予權重。兩個節點i和j之間的最短路徑長度dij可以定義為從i節點到j節點的所有路徑之間的最小距離之和。Floyd-Warshall算法可用于從任何固定點找到最短路徑的長度，其中i,j為任意網絡中的節點。用一個n×n的鄰接矩陣E定義電力系統網絡。在任何情況下，k次迭代都使用矩陣E(k-1)中的值，并將輸出的數據存儲在E(k)中。算法執行過程中進行n次迭代，最終結果存儲在n×n矩陣E(n)中。設E(0)=E為初始條件，矩陣E中的項(i,j)用eij來表示。當k取任意值，矩陣E(k)是有E(k-1)經過下列運算得到，這個運算稱為三步運算。此運算步驟為：若eij(k-1)≤eij(k-1)+eij(k-1)，eij(k)=eij(k-1)，否則eij(k)=eil(k-1)+elj(k-1)。

　　3.4中介線

　　本小節將中介線定義為經過特定點和通過特定的邊而得出的最短路徑。在本文的研究方法中，中介線可用以下方法來計算：

　　(1)首先計算從源節點i到所有其他節點的最短路徑;

　　(2)然后，從最遠的節點開始，對輸入樣本進行前向計算。在計算過程中，對每條線路賦予索引以示標記，然后將相鄰邊(相鄰邊共享公共節點)的索引相加后再加1。

　　(3)計算覆蓋了網絡中的所有節點，每條邊的索引給出了來自節點i的路徑的中間數;

　　(4)重復步驟(1)到(3)至不同的源節點，直到網絡中所有節點被覆蓋;

　　(5)所有每對節點間的迭代指數總和最小為節點間的最短路徑，也是網絡的中介線。

　　3.5易損線識別

　　前面的小節討論了識別線路脆弱性的定義和識別的方法。本章節列出了識別線路脆弱性的過程：

　　(1)根據前章節中的原則對電力系統進行建模，生成一個連接鄰接矩陣E;

　　(2)根據線路電抗對連接輸電線路賦予相應的權重;

　　(3)基于鄰接矩陣E和權值計算最短電氣路徑矩陣;

　　(4)以新的介數指標為基礎計算中介線;

　　(5)高介數值作為脆弱線路的標志;

　　(6)計算并比較在不同類型的攻擊下的電力網絡效率，驗證結果。

　　4電力網絡拓撲建模

　　4.1IEEE118系統仿真

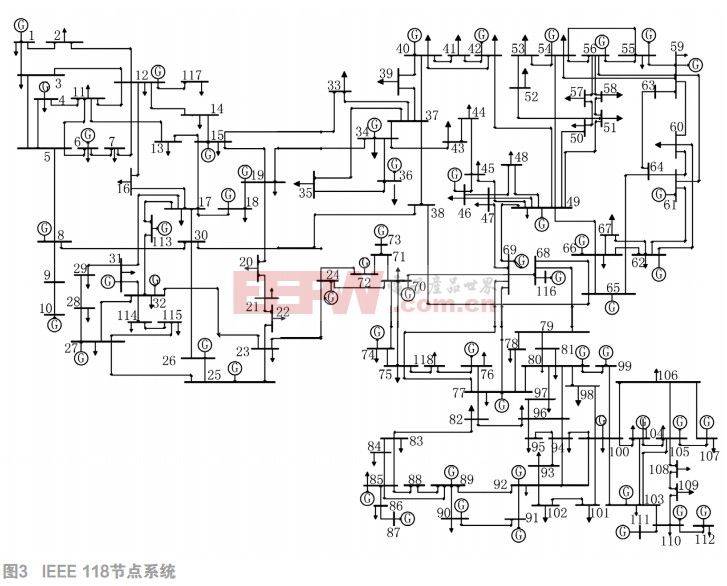
　　首先選取IEEE118系統節點測試仿真圖，如圖3。對系統分別進行隨機攻擊和蓄意攻擊，并識別其中的脆弱線路。表1列出了前十名的脆弱線路指標。

　　其次，對系統分別進行隨機攻擊和蓄意攻擊。隨機攻擊是隨機選取十條線路進行隨機移除，蓄意攻擊是對系統進行針對性攻擊，有目的的對十條高介數的線路依次移除，對結果進行驗證和記錄。

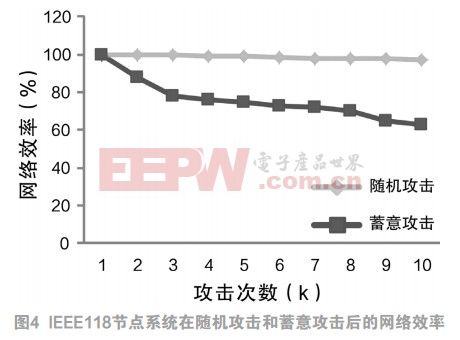
　　對IEEE118節點系統進行靈敏度分析，其結果繪制在圖4中。可以看出，在隨機攻擊下，網絡效率沒有受到太大的影響，即使在十次隨機攻擊之后，效率也下降了不到3%。另一方面，在網絡被進行了十次蓄意攻擊之后，網絡效率下降到近60%。

　　5結論和展望

　　本文在基于復雜網絡理論基礎上，提出了一種由新的介數指標判斷電力網絡線路脆弱性的方法。電力網絡可以根據介數指標中的位置和流經此線路的功率來識別易受攻擊的線路。在無損耗條件下，線路中的電抗值是衡量線路功率量的指標之一。通過對網絡模擬進行隨機攻擊和目標攻擊，最終結果驗證了新的介數指標能判斷線路脆弱性。研究表明，該系統對隨機攻擊具有較強的魯棒性，如果隨機選擇和移除元件，對系統的效率幾乎沒有影響。然而，在對有高介數指標的線路進行蓄意攻擊之后，網絡的效率急劇下降，IEEE118系統穩定性下降到60%。

　　對系統線路脆弱性的分析將有助于令電力系統更加穩定和可靠。今后的工作更加全面的分析系統的魯棒性和脆弱性，將本次研究中被忽略的其他參數，例如線路參數，如電壓、相角和電阻等因素也做一個全面分析和模擬。本文所提出新介數指標可以有效的找出網絡系統中的脆弱線路，更好的保護系統的穩定與安全。

　　參考文獻：

　　[1]P. Erdos and A. Renyi, "On the evolution of random graphs ," Publications of the Mathematical Institute of the Hungarian Academy of Sciences, no. 5, pp. 17-61 , 1960.

　　[2]D. J. Watts and S. H. Strogatz , "Collective dynamics of 'small-world'networks," Nature, vol.393, no. 6684 , pp. 440-442, 1998.

　　[3]D. J. Watts, Small Worlds: The Dynamics of Networks between Order and Randomness .Princeton University Press, 1999, pp. 11-40.

　　[4]V. Latora and M. Marchiori , "Efficient behaviour of small-world networks," Phys. Rev. uu..vol. 87, no. 19, 200.

　　[5] M. Ding and P. Han, "Reliability assessment to large-scale power grid based on smallworld topological model ," in Proc. International Conference on Power System Technology,PowerCon, 2006, pp. 1-5.

本文來源于中國科技期刊《電子產品世界》2019年第1期第45頁，歡迎您寫論文時引用，并注明出處