CT圖像重建算法的FPGA實現 (一)

1.3.5國內外研究現狀

同類課題所研究的技術基本上被國外所壟斷，國內尚未有人提出，國內現在所使用的技術是利用PC機上軟件來實現圖像的重構，所需時間較長，如果用FPGA來實現的話，速度可以提高數十乃至上百倍。

1.4研究背景及意義

在當今社會大力發展醫療衛生條件的背景下，許多醫院迫切需要先進的CT來為患者診斷病情，現在的CT技術被國外所壟斷，設備也都在200萬以上，只有極少數醫院有能力配備，所以急需研發具有自主知識產權的產品，把價格控制在50萬以內。CT的關鍵技術之一是快速斷層圖像重建技術，本課題的立足點就在于利用FPGA的高度并行性，實現CT斷層圖像重建算法，滿足實際產品速度要求，為實現CT國產化準備，推動社會醫療衛生條件的發展。

第二章 濾波反投影算法

2.1 濾波反投影算法介紹

盡管傅里葉切片定理提供了斷層成像重建的一個直接方案，在真正實現過程中，它提出了一些難題。首先，傅里葉空間中產生的采樣模式不是笛卡兒坐標的。傅里葉切片定理說明一次投影的傅里葉變換是二維傅里葉空間中通過原點的一條直線。結果，不同投影采樣落到極坐標柵格上。為了執行二維傅里葉變換，這些采樣不得不被插值或重新柵格化到一個笛卡兒坐標中。二維頻率域中的插值不像真實空間中的插值一樣直接。在真實空間里，一個插值誤差局限于像素所在的小區域。然而，對于頻域插值，這個特性不再有效，因為二維傅里葉空間中每個采樣表示某一個空間頻域(在水平和垂直方向上)。于是，在傅里葉空間中一個單獨采樣點上產生的誤差會影響整個圖像(經過傅里葉反變換后)的外貌。為闡明傅里葉域插值的敏感性，進行下面的簡單實驗。掃描一個肩部模體，并在512×512矩陣中重建，矩陣用f(x,y)表示，其中x=0，1，…512，y= 0，1，…，512。下一步，執行圖像的二維離散傅里葉變換，得到一個函數F(u,v)，其中u=0，1，…，511，v=0，1，…，511。注意F(u,v)是一個512×512復數矩陣。在該矩陣中，F(00)代表圖像的直流成分。如果簡單地進行函數F(u,v)的離散傅里葉反變換，將得到原始圖像f(x,y)。注意函數F(u,v)是我們試圖采用平行投影進行估計的量值(傅里葉切片定理)。

直接傅里葉域重建的另一缺點是進行目標重建的困難性。目標重建是在CT中常用的技術，用來檢查物體中一個小區域的精密細節。如果能以某種方式把重建“聚焦”在感興趣區，物體的細節就可以更好地顯現。采用直接傅里葉重建方法，需要用大量的0填充F(u,v)，以進行必要的頻率域插值。傅里葉反變換的大小和目標ROI的尺寸成反比。對非常小的ROI，矩陣尺寸龐大以至無法管理。盡管其他技術可以用來克服其中一些困難，這些技術的實現仍不直截了當。因此，必須研究傅里葉切片定理的替代實現方法。濾波反投影算法是目前得到廣泛應用的基于變換法的圖像重建算法，它具有重建速度快、空間和密度分辨率高等優點，缺點是對投影數據的完備性要求較高[7]，從數學上講，只有獲得被檢試件所有的Radon變換數據(完全投影數據)后才能精確重建其切片圖像。

2.2 濾波反投影算法公式的推導

我們從傅里葉變換和傅里葉反變換是共扼算子這一眾所周知的事實開始。圖像函數f(x,y)可以通過傅里葉反變換從它的傅里葉變換F(u,v)中恢復，

(2.1)

與推導傅里葉切片定理時進行的坐標變換類似，我們從笛卡兒直角坐標(u,v)轉換到極坐標

。

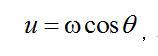
坐標轉換的目的是以更自然的數據采集形式表達數值F(u,v)。坐標轉換如下：

，

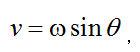
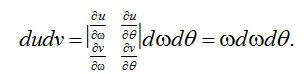
， (2.2)

和

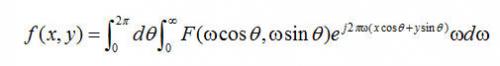
(2.3)

將等式(2.2)和(2.3)帶入到(3.1)，得到

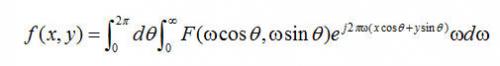
(2.4)

利用公式

中描述的傅里葉切片定理，我們用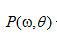代替，建立如下關系：

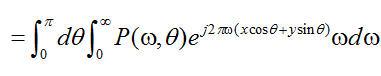
(2.5)

.

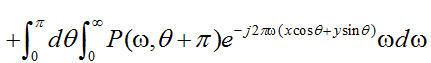
對于平行采樣幾何束，在投影采樣中存在一個微妙的對稱性：

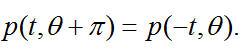
(2.6)

通過研究一組相差180°的平行束的采樣幾何，這個特性可以很容易理解。兩組投影正好代表同一組射線路徑。基于傅里葉變換的特性，對于相應的傅里葉變換對來說，存在一個簡單關系：

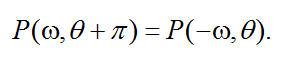
(2.7)

將等式(2.7)代入等式(2.5)，我們得到下面等式：

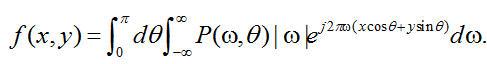
(2.8)

通過在旋轉坐標系(s,t)中表達上面的等式，并利用等式：

.

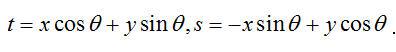
中指出的關系，我們得到下面等式：

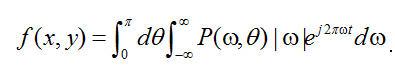
. (2.9)

這里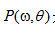，是在角度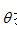投影的傅里葉變換。內部積分是數值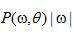的傅里葉反變換。在空間域，它代表一個經頻域響應為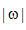的函數濾波后的投影。我們稱之為“濾波投影”。

如果用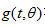標記等式(2.9)的內部積分所代表的角上的濾波投影：

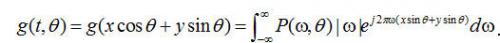
. (2.10)

等式(2.8)可以下面形式重寫

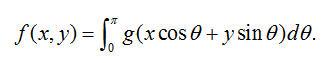
(2.11)

變量是從點(x,y)到一條通過坐標系原點，并與x軸成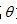角的直線的距離。等式(2.11)說明，重建圖像f(x,y)在位置(x,y)，是通過該點的所有濾波投影采樣的累加。另外，我們還可以選擇關注一個特定濾波投影采樣，研究它對重建圖像的貢獻。因為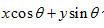代表與產生投影采樣的射線路徑重疊的一條直線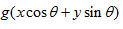，的強度沿著直線均勻地加到重建圖像。結果，濾波投影采樣的值沿著整個直線路徑被“涂抹”或“疊加”。

我們還可以給出濾波反投影方法的一個直觀解釋。基于傅里葉切片定理，物體的二維傅里葉變換是通過將許多一維傅里葉變換拼起來得到的。理論上，如果假定一次投影的傅里葉變換形狀像一個切成薄片的“派”，我們可以簡單地把每個楔子插入適當位置，以得到物體的一個二維傅里葉變換。不幸的是，每個投影傅里葉變換形狀類似在頻率空間的一個長條。如果簡單地計算所有投影傅里葉變換的和(假設在角度上等間隔)，中心區域被人為地增強，而外側區域數值不足。為了用條形區域估計“派”狀區域，我們可以給條形傅里葉變換乘以一個函數，該函數在靠近中心位置強度低，靠近邊緣時強度高。例如，可以將投影的傅里葉變換與該頻率處“派”狀楔子的寬度相乘。如果假設N個投影在180°內均勻間隔，每個楔子的寬度在頻率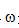是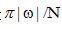。權重函數的最終作用是加權長條的累加與“派”狀楔子的累加具有相同的“質量”。[8]