CT圖像重建算法的FPGA實(shí)現(xiàn) (二)

2.3 計(jì)算機(jī)實(shí)現(xiàn)的理論研究

在程序中，濾波反投影算法的步驟為：

投影數(shù)據(jù)采集

對(duì)投影數(shù)據(jù)做FFT變換

濾波

反投影數(shù)據(jù)

逆FFT變換

等式(2.8)不能以它現(xiàn)有形式直接實(shí)現(xiàn)，只要考慮公式(2.10)的解釋，就很容易理解這一點(diǎn)。基于傅里葉變換的特性，我們知道在傅里葉域中兩個(gè)函數(shù)相乘等價(jià)于兩個(gè)相應(yīng)空間域函數(shù)的卷積。 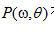在空間域中的對(duì)應(yīng)函數(shù)是被測(cè)平行投影 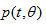。對(duì)應(yīng)濾波函數(shù) 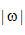的空間領(lǐng)域(或沖激響應(yīng)) 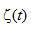，就是該函數(shù)的傅里葉反變換，

(2.12)

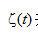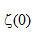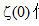并不存在。必須研究一個(gè)代替方法。一個(gè)這樣的方法是把有限帶寬函數(shù)引入公式中。例如在上式中設(shè)置t=0，讓我們考慮 的值。 代表在曲線 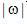下面的面積。當(dāng) 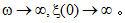。因此，等式(2.8)不能以它現(xiàn)有形式實(shí)現(xiàn)。必須研究一個(gè)代替方法。一個(gè)這樣的方法是把有限帶寬函數(shù)引入公式中。

假設(shè)投影的傅里葉變換是有限帶寬的。換句話說(shuō)，在頻率間隔 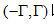以外能量為0.在這個(gè)假設(shè)下，等式(2.10)可以按下面形式表示：

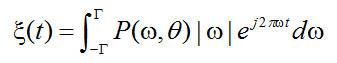
(2.13)

等式(2.13)指出，要計(jì)算濾波的投影 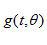，只需要進(jìn)行投影 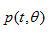的傅里葉變換以得到 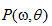，在 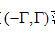范圍內(nèi)乘以 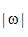，并進(jìn)行傅里葉反變換。不幸的是，有兩個(gè)因素使這個(gè)看似簡(jiǎn)單的問(wèn)題變得復(fù)雜：被截?cái)嗟臑V波核的離散化以及環(huán)狀卷積的性質(zhì)。要徹底理解濾波核問(wèn)題，讓我們首先在空間域中推導(dǎo)理想濾波核。為保證無(wú)混疊采樣，投影帶寬T必須滿足Nyquist(奈奎斯特)采樣準(zhǔn)則：

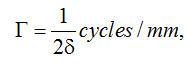
(2.14)

其中 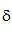是投影采樣間隔(單位為 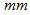)。在該條件下，初始的斜變函數(shù) 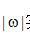實(shí)際上是與窗函數(shù) 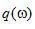相乘：

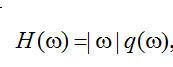
(2.15)

其中

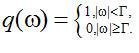
濾波函數(shù) 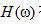在圖2.1中描繪。現(xiàn)在，濾波器沖激響應(yīng)可以描述如下

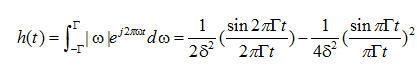
. (2.16)

注意由于 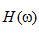的 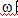的一個(gè)實(shí)偶函數(shù)，相應(yīng)的沖激響應(yīng) 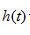也是t的一個(gè)實(shí)偶函數(shù)。

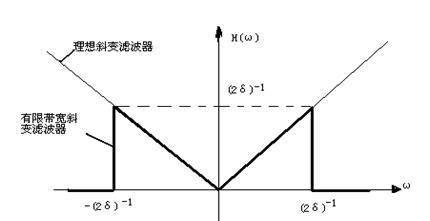
圖2.1 有限帶寬斜變?yōu)V波器的頻率表示

注意，投影以間隔 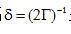采樣。根據(jù)卷積理論，等式(2.9)可以寫為

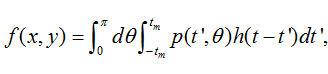
(2.17)

其中 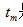是滿足條件

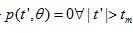
的 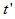值。這里，我們利用被掃描物體具有有限空間緊支集這一事實(shí)。在濾波投影的離散實(shí)現(xiàn)時(shí)，我們只對(duì)在 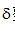整數(shù)倍處的濾波數(shù)值感興趣。把 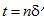代入等式(2.16)中，得到

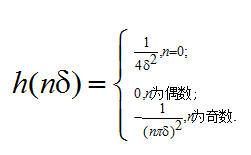
(2.18)

濾波函數(shù)的沖激響應(yīng)在圖2.2中畫出。在該圖中，我們?cè)O(shè) 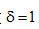。如果用

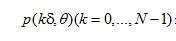
表示在角度 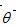下投影的離散采樣，等式(2.10)中描述的濾波投影可以表達(dá)為一個(gè)空間域卷積：

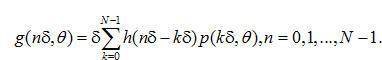
(2.19)

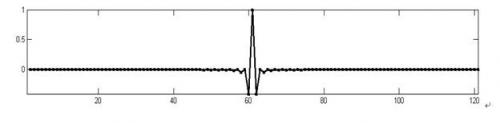
圖2.2 斜邊濾波器的沖激響應(yīng)

這里，我們利用了每個(gè)投影在空間上具有有限緊支集的事實(shí)。即在下標(biāo)范圍以外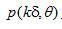， 為0.這意味著，要確定 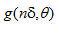，我們只需利用在范圍 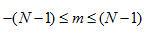內(nèi)的 。

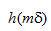盡管等式(2.19)的離散卷積實(shí)現(xiàn)可以直接得到被濾波的投影，當(dāng)N很大時(shí)，往往在頻率域中執(zhí)行運(yùn)算效率更高[使用快速傅里葉變換(FFT)運(yùn)算]。對(duì)于目前一臺(tái)典型的CT掃描機(jī)，一次單獨(dú)投影的采樣數(shù)N接近1000.因此，我們希望得到 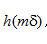序列的頻率域形式。在有限范圍內(nèi) 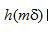的離散傅里葉變換 與等式(2.15)描述的 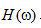不同，如圖2.3所示。二者之間主要差別是直流成分。盡管差相當(dāng)小，它對(duì)重建圖像CT數(shù)準(zhǔn)確度的影響不能忽略。

現(xiàn)在我們考慮循環(huán)卷積[9]的問(wèn)題。等式(2.10)中描述的原始濾波運(yùn)算需要一個(gè)非周期性的卷積。當(dāng)這個(gè)運(yùn)算在頻率域中執(zhí)行時(shí)，只能是周期性或循環(huán)卷積。如果直接實(shí)線前面所述的運(yùn)算序列，可能產(chǎn)生干涉?zhèn)蜗瘛＿@就是所謂的卷繞(warp-around)效應(yīng)，或者周期間干涉。為了避免偽像，需要在傅里葉變換和濾波運(yùn)算之前為每個(gè)投影填補(bǔ)足夠數(shù)量的零。零的最少數(shù)目必須等于初始投影采樣數(shù)減1(即N-1)。

圖2.3中所示斜變?yōu)V波器

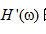的特性表明，相對(duì)于低頻成分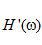， 更突出強(qiáng)調(diào)高頻成分。事實(shí)上，斜變?yōu)V波器表現(xiàn)有些好像微分運(yùn)算符。因此，可以把濾波運(yùn)算想象為一個(gè)反卷積過(guò)程，去掉了反投影產(chǎn)生的模糊。

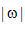函數(shù)(實(shí)線)和有限帶寬斜變?yōu)V波器傅里葉變換(虛線)的比較在等式(2.15)中，我們采用了一個(gè)簡(jiǎn)單的矩形窗函數(shù)來(lái)限制濾波核。可以另外修改窗函數(shù)，以改變?yōu)V波器的頻率響應(yīng)。實(shí)際應(yīng)用中，窗函數(shù)經(jīng)常被作為一個(gè)工具，用來(lái)修改重建圖像的噪聲特性，以實(shí)現(xiàn)空間分辨率和圖像噪聲之間的折中。

在許多用于數(shù)值計(jì)算和圖像的高級(jí)語(yǔ)言軟件系統(tǒng)中，如Matlab(The MathWorks,Natick,MA)或IDL(Research Systems,Inc,Boulder,CO),矢量或矩陣可以直接表示成變量。還可以針對(duì)矢量定義不同運(yùn)算符。在這樣的環(huán)境中，平行反投影的實(shí)現(xiàn)變得相當(dāng)容易。對(duì)于每個(gè)被測(cè)投影(在數(shù)據(jù)預(yù)處理或預(yù)調(diào)理后)，投影被填補(bǔ)足夠多的0以避免“周期間”干擾。對(duì)補(bǔ)零后的投影進(jìn)行傅里葉變換，并且被變換的投影乘以一個(gè)濾波函數(shù)[10]。然后，對(duì)結(jié)果進(jìn)行傅里葉反變換，得到一個(gè)被濾波的投影。該投影被反投影(通過(guò)“像素驅(qū)動(dòng)”或“射線驅(qū)動(dòng)”)到圖像矩陣。為了提高空間分辨率，濾波投影經(jīng)常在反投影過(guò)程之前進(jìn)行預(yù)插值。在投影數(shù)據(jù)集合中對(duì)每次投影重復(fù)整個(gè)過(guò)程。圖2.4顯示一個(gè)流程圖，描述了對(duì)于平行束投影[11]的重建過(guò)程。