加法器電路原理圖解

在計數體制中，通常用的是十進制，它有0，1，2，3，…，9十個數碼，用它們來組成一個數。但在數字電路中，為了把電路的兩個狀態(1態和0態)和數碼對應起來，采用二進制較為方便，二進制只有0和1兩個數碼。

二進制加法器是數字電路的基本部件之一。二進制加法運算同邏輯加法運算的含義是不同的。前者是數的運算，而后者表示邏輯關系。二進制加法是“逢二進一”，即1+1=10，而邏輯加則為1+1=1。

1、半加器

所謂“半加”，就是只求本位的和，暫不管低位送來的進位數。半加器的邏輯狀態表見表1。

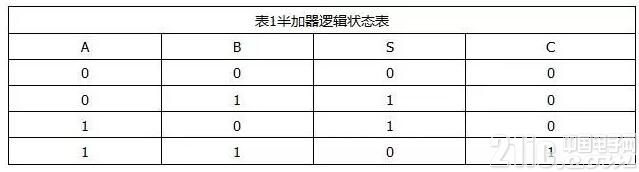
表1半加器邏輯狀態表

其中，A和B是相加的兩個數，S是半加和數，C是進位數。

由邏輯狀態表可寫出邏輯式：

并由此畫出圖1(a)的邏輯圖。圖1(b)是半加器的邏輯符號。

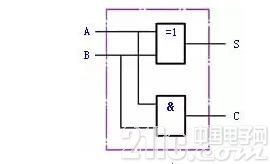
(a)邏輯圖

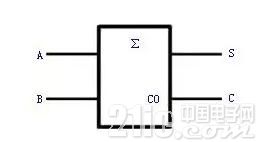
(b)邏輯符號

圖1半加器邏輯圖及其邏輯符號

2、全加器

當多位數相加時，半加器可用于最低位求和，并給出進位數。第二位的相加有兩個待加數，還有一個來自低位送來的進位數。這三個數相加，得出本位和數(全加和數)和進位數，這就是“全加”，表2是全加器的邏輯狀態表

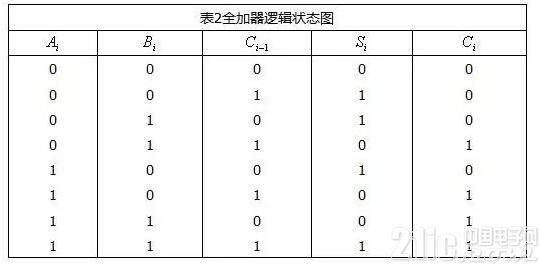
全加器可用兩個半加器和一個或門組成，如圖2(a)所示。在第一個半加器中相加，得出的結果再和在第二個半加器中相加，即得出全加和。兩個半加器的進位數通過或門輸出作為本位的進位數。圖2(b)是全加器的邏輯符號。

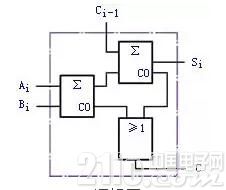
(a)邏輯圖

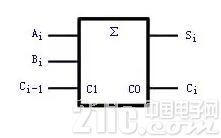
(b)邏輯符號

圖2 全加器邏輯圖及其邏輯符號

例1、用4個全加器組成一個邏輯電路以實現兩個4位的二進制數A—1101(十進制為13)和B—1011(十進制為11)的加法運算。

解：

邏輯電路如圖3所示，和數是S—11000(十進制數為24)。根據全加器的邏輯狀態表自行分析。

這種全加器的任意一位的加法運算，都必須等到低位加法完成送來進位時才能進行。這種進位方式稱為串行進位，它的缺點是運算速度慢，但其電路比較簡單，因此在對運算速度要求不高的設備中，仍不失為一種可取的全加器。T692集成加法器就是這種串行加法器。

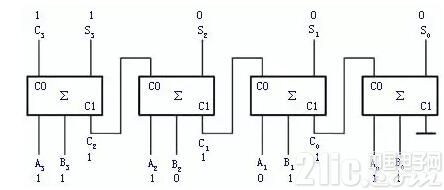
圖3 例1的邏輯圖