標簽傳播算法（Label Propagation）及Python實現

眾所周知，機器學習可以大體分為三大類：監督學習、非監督學習和半監督學習。監督學習可以認為是我們有非常多的labeled標注數據來train一個模型，期待這個模型能學習到數據的分布，以期對未來沒有見到的樣本做預測。那這個性能的源頭--訓練數據，就顯得非常感覺。你必須有足夠的訓練數據，以覆蓋真正現實數據中的樣本分布才可以，這樣學習到的模型才有意義。那非監督學習就是沒有任何的labeled數據，就是平時所說的聚類了，利用他們本身的數據分布，給他們劃分類別。而半監督學習，顧名思義就是處于兩者之間的，只有少量的labeled數據，我們試圖從這少量的labeled數據和大量的unlabeled數據中學習到有用的信息。

一、半監督學習

半監督學習(Semi-supervised learning)發揮作用的場合是：你的數據有一些有label，一些沒有。而且一般是絕大部分都沒有，只有少許幾個有label。半監督學習算法會充分的利用unlabeled數據來捕捉我們整個數據的潛在分布。它基于三大假設：

1)Smoothness平滑假設：相似的數據具有相同的label。

2)Cluster聚類假設：處于同一個聚類下的數據具有相同label。

3)Manifold流形假設：處于同一流形結構下的數據具有相同label。

例如下圖，只有兩個labeled數據，如果直接用他們來訓練一個分類器，例如LR或者SVM，那么學出來的分類面就是左圖那樣的。如果現實中，這個數據是右圖那邊分布的話，豬都看得出來，左圖訓練的這個分類器爛的一塌糊涂、慘不忍睹。因為我們的labeled訓練數據太少了，都沒辦法覆蓋我們未來可能遇到的情況。但是，如果右圖那樣，把大量的unlabeled數據(黑色的)都考慮進來，有個全局觀念，牛逼的算法會發現，哎喲，原來是兩個圈圈(分別處于兩個圓形的流形之上)!那算法就很聰明，把大圈的數據都歸類為紅色類別，把內圈的數據都歸類為藍色類別。因為，實踐中，labeled數據是昂貴，很難獲得的，但unlabeled數據就不是了，寫個腳本在網上爬就可以了，因此如果能充分利用大量的unlabeled數據來輔助提升我們的模型學習，這個價值就非常大。

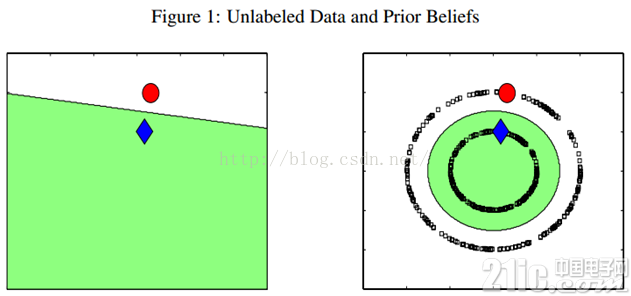
半監督學習算法有很多，下面我們介紹最簡單的標簽傳播算法(label propagation)，最喜歡簡單了，哈哈。

二、標簽傳播算法

標簽傳播算法(label propagation)的核心思想非常簡單：相似的數據應該具有相同的label。LP算法包括兩大步驟：1)構造相似矩陣;2)勇敢的傳播吧。

2.1、相似矩陣構建

LP算法是基于Graph的，因此我們需要先構建一個圖。我們為所有的數據構建一個圖，圖的節點就是一個數據點，包含labeled和unlabeled的數據。節點i和節點j的邊表示他們的相似度。這個圖的構建方法有很多，這里我們假設這個圖是全連接的，節點i和節點j的邊權重為：

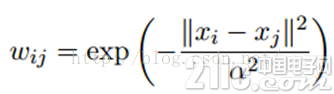
這里，α是超參。

還有個非常常用的圖構建方法是knn圖，也就是只保留每個節點的k近鄰權重，其他的為0，也就是不存在邊，因此是稀疏的相似矩陣。

2.2、LP算法

標簽傳播算法非常簡單：通過節點之間的邊傳播label。邊的權重越大，表示兩個節點越相似，那么label越容易傳播過去。我們定義一個NxN的概率轉移矩陣P：

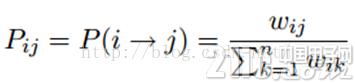
Pij表示從節點i轉移到節點j的概率。假設有C個類和L個labeled樣本，我們定義一個LxC的label矩陣YL，第i行表示第i個樣本的標簽指示向量，即如果第i個樣本的類別是j，那么該行的第j個元素為1，其他為0。同樣，我們也給U個unlabeled樣本一個UxC的label矩陣YU。把他們合并，我們得到一個NxC的soft label矩陣F=[YL;YU]。soft label的意思是，我們保留樣本i屬于每個類別的概率，而不是互斥性的，這個樣本以概率1只屬于一個類。當然了，最后確定這個樣本i的類別的時候，是取max也就是概率最大的那個類作為它的類別的。那F里面有個YU，它一開始是不知道的，那最開始的值是多少?無所謂，隨便設置一個值就可以了。

千呼萬喚始出來，簡單的LP算法如下：

1)執行傳播：F=PF

2)重置F中labeled樣本的標簽：FL=YL

3)重復步驟1)和2)直到F收斂。

步驟1)就是將矩陣P和矩陣F相乘，這一步，每個節點都將自己的label以P確定的概率傳播給其他節點。如果兩個節點越相似(在歐式空間中距離越近)，那么對方的label就越容易被自己的label賦予，就是更容易拉幫結派。步驟2)非常關鍵，因為labeled數據的label是事先確定的，它不能被帶跑，所以每次傳播完，它都得回歸它本來的label。隨著labeled數據不斷的將自己的label傳播出去，最后的類邊界會穿越高密度區域，而停留在低密度的間隔中。相當于每個不同類別的labeled樣本劃分了勢力范圍。

2.3、變身的LP算法

我們知道，我們每次迭代都是計算一個soft label矩陣F=[YL;YU]，但是YL是已知的，計算它沒有什么用，在步驟2)的時候，還得把它弄回來。我們關心的只是YU，那我們能不能只計算YU呢?Yes。我們將矩陣P做以下劃分：

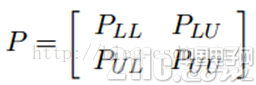
這時候，我們的算法就一個運算：

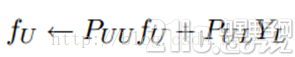
迭代上面這個步驟直到收斂就ok了，是不是很cool。可以看到FU不但取決于labeled數據的標簽及其轉移概率，還取決了unlabeled數據的當前label和轉移概率。因此LP算法能額外運用unlabeled數據的分布特點。

這個算法的收斂性也非常容易證明，具體見參考文獻[1]。實際上，它是可以收斂到一個凸解的：

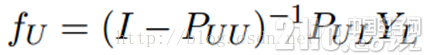
所以我們也可以直接這樣求解，以獲得最終的YU。但是在實際的應用過程中，由于矩陣求逆需要O(n3)的復雜度，所以如果unlabeled數據非常多，那么I – PUU矩陣的求逆將會非常耗時，因此這時候一般選擇迭代算法來實現。

三、LP算法的Python實現

Python環境的搭建就不嗦了，可以參考前面的博客。需要額外依賴的庫是經典的numpy和matplotlib。代碼中包含了兩種圖的構建方法：RBF和KNN指定。同時，自己生成了兩個toy數據庫：兩條長形形狀和兩個圈圈的數據。第四部分我們用大點的數據庫來做實驗，先簡單的可視化驗證代碼的正確性，再前線。

算法代碼：

#***************************************************************************

#*

#* Description: label propagation

#* Author: Zou Xiaoyi (zouxy09@qq.com)

#* Date: 2015-10-15

#* HomePage: http://blog.csdn.net/zouxy09

#*

#**************************************************************************

import time

import numpy as np

# return k neighbors index

def navie_knn(dataSet, query, k):

numSamples = dataSet.shape[0]

## step 1: calculate Euclidean distance

diff = np.tile(query, (numSamples, 1)) - dataSet

squaredDiff = diff ** 2

squaredDist = np.sum(squaredDiff, axis = 1) # sum is performed by row

## step 2: sort the distance

sortedDistIndices = np.argsort(squaredDist)

if k > len(sortedDistIndices):

k = len(sortedDistIndices)

return sortedDistIndices[0:k]

# build a big graph (normalized weight matrix)

def buildGraph(MatX, kernel_type, rbf_sigma = None, knn_num_neighbors = None):

num_samples = MatX.shape[0]

affinity_matrix = np.zeros((num_samples, num_samples), np.float32)

if kernel_type == 'rbf':

if rbf_sigma == None:

raise ValueError('You should input a sigma of rbf kernel!')

for i in xrange(num_samples):

row_sum = 0.0

for j in xrange(num_samples):

diff = MatX[i, :] - MatX[j, :]

affinity_matrix[i][j] = np.exp(sum(diff**2) / (-2.0 * rbf_sigma**2))

row_sum += affinity_matrix[i][j]

affinity_matrix[i][:] /= row_sum

elif kernel_type == 'knn':

if knn_num_neighbors == None:

raise ValueError('You should input a k of knn kernel!')

for i in xrange(num_samples):

k_neighbors = navie_knn(MatX, MatX[i, :], knn_num_neighbors)

affinity_matrix[i][k_neighbors] = 1.0 / knn_num_neighbors

else:

raise NameError('Not support kernel type! You can use knn or rbf!')

return affinity_matrix

# label propagation

def labelPropagation(Mat_Label, Mat_Unlabel, labels, kernel_type = 'rbf', rbf_sigma = 1.5,

knn_num_neighbors = 10, max_iter = 500, tol = 1e-3):

# initialize

num_label_samples = Mat_Label.shape[0]

num_unlabel_samples = Mat_Unlabel.shape[0]

num_samples = num_label_samples + num_unlabel_samples

labels_list = np.unique(labels)

num_classes = len(labels_list)

MatX = np.vstack((Mat_Label, Mat_Unlabel))

clamp_data_label = np.zeros((num_label_samples, num_classes), np.float32)

for i in xrange(num_label_samples):

clamp_data_label[i][labels[i]] = 1.0

label_function = np.zeros((num_samples, num_classes), np.float32)

label_function[0 : num_label_samples] = clamp_data_label

label_function[num_label_samples : num_samples] = -1

# graph construction

affinity_matrix = buildGraph(MatX, kernel_type, rbf_sigma, knn_num_neighbors)

# start to propagation

iter = 0; pre_label_function = np.zeros((num_samples, num_classes), np.float32)

changed = np.abs(pre_label_function - label_function).sum()

while iter max_iter and changed > tol:

if iter % 1 == 0:

print ---> Iteration %d/%d, changed: %f % (iter, max_iter, changed)

pre_label_function = label_function

iter += 1

# propagation

label_function = np.dot(affinity_matrix, label_function)

# clamp

label_function[0 : num_label_samples] = clamp_data_label

# check converge

changed = np.abs(pre_label_function - label_function).sum()

# get terminate label of unlabeled data

unlabel_data_labels = np.zeros(num_unlabel_samples)

for i in xrange(num_unlabel_samples):

unlabel_data_labels[i] = np.argmax(label_function[i+num_label_samples])

return unlabel_data_labels

測試代碼：

#***************************************************************************

#*

#* Description: label propagation

#* Author: Zou Xiaoyi (zouxy09@qq.com)

#* Date: 2015-10-15

#* HomePage: http://blog.csdn.net/zouxy09

#*

#**************************************************************************

import time

import math

import numpy as np

from label_propagation import labelPropagation

# show

def show(Mat_Label, labels, Mat_Unlabel, unlabel_data_labels):

import matplotlib.pyplot as plt

for i in range(Mat_Label.shape[0]):

if int(labels[i]) == 0:

plt.plot(Mat_Label[i, 0], Mat_Label[i, 1], 'Dr')

elif int(labels[i]) == 1:

plt.plot(Mat_Label[i, 0], Mat_Label[i, 1], 'Db')

else:

plt.plot(Mat_Label[i, 0], Mat_Label[i, 1], 'Dy')

for i in range(Mat_Unlabel.shape[0]):

if int(unlabel_data_labels[i]) == 0:

plt.plot(Mat_Unlabel[i, 0], Mat_Unlabel[i, 1], 'or')

elif int(unlabel_data_labels[i]) == 1:

plt.plot(Mat_Unlabel[i, 0], Mat_Unlabel[i, 1], 'ob')

else:

plt.plot(Mat_Unlabel[i, 0], Mat_Unlabel[i, 1], 'oy')

plt.xlabel('X1'); plt.ylabel('X2')

plt.xlim(0.0, 12.)

plt.ylim(0.0, 12.)

plt.show()

def loadCircleData(num_data):

center = np.array([5.0, 5.0])

radiu_inner = 2

radiu_outer = 4

num_inner = num_data / 3

num_outer = num_data - num_inner

data = []

theta = 0.0

for i in range(num_inner):

pho = (theta % 360) * math.pi / 180

tmp = np.zeros(2, np.float32)

tmp[0] = radiu_inner * math.cos(pho) + np.random.rand(1) + center[0]

tmp[1] = radiu_inner * math.sin(pho) + np.random.rand(1) + center[1]

data.append(tmp)

theta += 2

theta = 0.0

for i in range(num_outer):

pho = (theta % 360) * math.pi / 180

tmp = np.zeros(2, np.float32)

tmp[0] = radiu_outer * math.cos(pho) + np.random.rand(1) + center[0]

tmp[1] = radiu_outer * math.sin(pho) + np.random.rand(1) + center[1]

data.append(tmp)

theta += 1

Mat_Label = np.zeros((2, 2), np.float32)

Mat_Label[0] = center + np.array([-radiu_inner + 0.5, 0])

Mat_Label[1] = center + np.array([-radiu_outer + 0.5, 0])

labels = [0, 1]

Mat_Unlabel = np.vstack(data)

return Mat_Label, labels, Mat_Unlabel

def loadBandData(num_unlabel_samples):

#Mat_Label = np.array([[5.0, 2.], [5.0, 8.0]])

#labels = [0, 1]

#Mat_Unlabel = np.array([[5.1, 2.], [5.0, 8.1]])

Mat_Label = np.array([[5.0, 2.], [5.0, 8.0]])

labels = [0, 1]

num_dim = Mat_Label.shape[1]

Mat_Unlabel = np.zeros((num_unlabel_samples, num_dim), np.float32)

Mat_Unlabel[:num_unlabel_samples/2, :] = (np.random.rand(num_unlabel_samples/2, num_dim) - 0.5) * np.array([3, 1]) + Mat_Label[0]

Mat_Unlabel[num_unlabel_samples/2 : num_unlabel_samples, :] = (np.random.rand(num_unlabel_samples/2, num_dim) - 0.5) * np.array([3, 1]) + Mat_Label[1]

return Mat_Label, labels, Mat_Unlabel

# main function

if __name__ == __main__:

num_unlabel_samples = 800

#Mat_Label, labels, Mat_Unlabel = loadBandData(num_unlabel_samples)

Mat_Label, labels, Mat_Unlabel = loadCircleData(num_unlabel_samples)

## Notice: when use 'rbf' as our kernel, the choice of hyper parameter 'sigma' is very import! It should be

## chose according to your dataset, specific the distance of two data points. I think it should ensure that

## each point has about 10 knn or w_i,j is large enough. It also influence the speed of converge. So, may be

## 'knn' kernel is better!

#unlabel_data_labels = labelPropagation(Mat_Label, Mat_Unlabel, labels, kernel_type = 'rbf', rbf_sigma = 0.2)

unlabel_data_labels = labelPropagation(Mat_Label, Mat_Unlabel, labels, kernel_type = 'knn', knn_num_neighbors = 10, max_iter = 400)

show(Mat_Label, labels, Mat_Unlabel, unlabel_data_labels)

該注釋的，代碼都注釋的，有看不明白的，歡迎交流。不同迭代次數時候的結果如下：

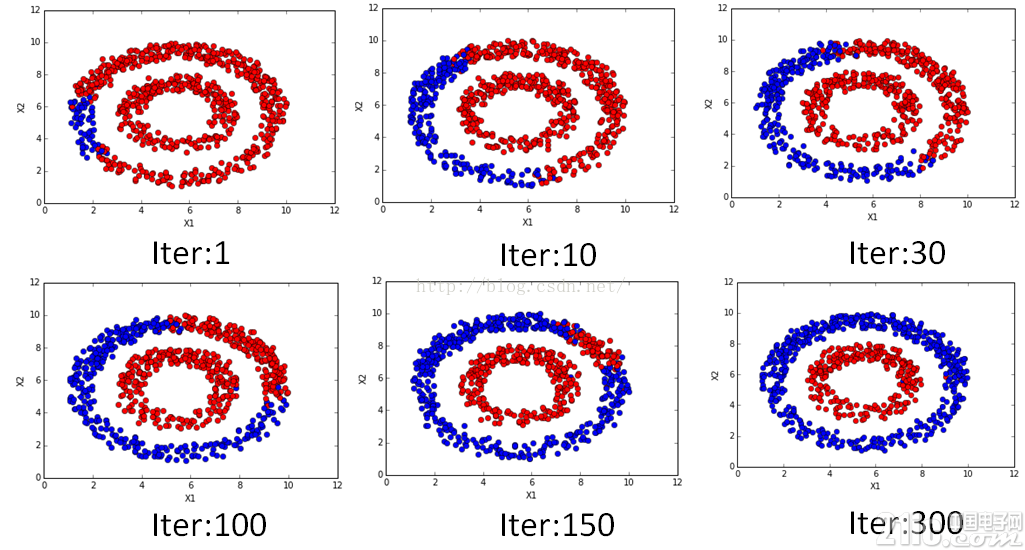
是不是很漂亮的傳播過程?!在數值上也是可以看到隨著迭代的進行逐漸收斂的，迭代的數值變化過程如下：

---> Iteration 0/400, changed: 1602.000000

---> Iteration 1/400, changed: 6.300182

---> Iteration 2/400, changed: 5.129996

---> Iteration 3/400, changed: 4.301994

---> Iteration 4/400, changed: 3.819295

---> Iteration 5/400, changed: 3.501743

---> Iteration 6/400, changed: 3.277122

---> Iteration 7/400, changed: 3.105952

---> Iteration 8/400, changed: 2.967030

---> Iteration 9/400, changed: 2.848606

---> Iteration 10/400, changed: 2.743997

---> Iteration 11/400, changed: 2.649270

---> Iteration 12/400, changed: 2.562057

---> Iteration 13/400, changed: 2.480885

---> Iteration 14/400, changed: 2.404774

---> Iteration 15/400, changed: 2.333075

---> Iteration 16/400, changed: 2.265301

---> Iteration 17/400, changed: 2.201107

---> Iteration 18/400, changed: 2.140209

---> Iteration 19/400, changed: 2.082354

---> Iteration 20/400, changed: 2.027376

---> Iteration 21/400, changed: 1.975071

---> Iteration 22/400, changed: 1.925286

---> Iteration 23/400, changed: 1.877894

---> Iteration 24/400, changed: 1.832743

---> Iteration 25/400, changed: 1.789721

---> Iteration 26/400, changed: 1.748706

---> Iteration 27/400, changed: 1.709593

---> Iteration 28/400, changed: 1.672284

---> Iteration 29/400, changed: 1.636668

---> Iteration 30/400, changed: 1.602668

---> Iteration 31/400, changed: 1.570200

---> Iteration 32/400, changed: 1.539179

---> Iteration 33/400, changed: 1.509530

---> Iteration 34/400, changed: 1.481182

---> Iteration 35/400, changed: 1.454066

---> Iteration 36/400, changed: 1.428120

---> Iteration 37/400, changed: 1.403283

---> Iteration 38/400, changed: 1.379502

---> Iteration 39/400, changed: 1.356734

---> Iteration 40/400, changed: 1.334906

---> Iteration 41/400, changed: 1.313983

---> Iteration 42/400, changed: 1.293921

---> Iteration 43/400, changed: 1.274681

---> Iteration 44/400, changed: 1.256214

---> Iteration 45/400, changed: 1.238491

---> Iteration 46/400, changed: 1.221474

---> Iteration 47/400, changed: 1.205126

---> Iteration 48/400, changed: 1.189417

---> Iteration 49/400, changed: 1.174316

---> Iteration 50/400, changed: 1.159804

---> Iteration 51/400, changed: 1.145844

---> Iteration 52/400, changed: 1.132414

---> Iteration 53/400, changed: 1.119490

---> Iteration 54/400, changed: 1.107032

---> Iteration 55/400, changed: 1.095054

---> Iteration 56/400, changed: 1.083513

---> Iteration 57/400, changed: 1.072397

---> Iteration 58/400, changed: 1.061671

---> Iteration 59/400, changed: 1.051324

---> Iteration 60/400, changed: 1.041363

---> Iteration 61/400, changed: 1.031742

---> Iteration 62/400, changed: 1.022459

---> Iteration 63/400, changed: 1.013494

---> Iteration 64/400, changed: 1.004836

---> Iteration 65/400, changed: 0.996484

---> Iteration 66/400, changed: 0.988407

---> Iteration 67/400, changed: 0.980592

---> Iteration 68/400, changed: 0.973045

---> Iteration 69/400, changed: 0.965744

---> Iteration 70/400, changed: 0.958682

---> Iteration 71/400, changed: 0.951848

---> Iteration 72/400, changed: 0.945227

---> Iteration 73/400, changed: 0.938820

---> Iteration 74/400, changed: 0.932608

---> Iteration 75/400, changed: 0.926590

---> Iteration 76/400, changed: 0.920765

---> Iteration 77/400, changed: 0.915107

---> Iteration 78/400, changed: 0.909628

---> Iteration 79/400, changed: 0.904309

---> Iteration 80/400, changed: 0.899143

---> Iteration 81/400, changed: 0.894122

---> Iteration 82/400, changed: 0.889259

---> Iteration 83/400, changed: 0.884530

---> Iteration 84/400, changed: 0.879933

---> Iteration 85/400, changed: 0.875464

---> Iteration 86/400, changed: 0.871121

---> Iteration 87/400, changed: 0.866888

---> Iteration 88/400, changed: 0.862773

---> Iteration 89/400, changed: 0.858783

---> Iteration 90/400, changed: 0.854879

---> Iteration 91/400, changed: 0.851084

---> Iteration 92/400, changed: 0.847382

---> Iteration 93/400, changed: 0.843779

---> Iteration 94/400, changed: 0.840274

---> Iteration 95/400, changed: 0.836842

---> Iteration 96/400, changed: 0.833501

---> Iteration 97/400, changed: 0.830240

---> Iteration 98/400, changed: 0.827051

---> Iteration 99/400, changed: 0.823950

---> Iteration 100/400, changed: 0.820906

---> Iteration 101/400, changed: 0.817946

---> Iteration 102/400, changed: 0.815053

---> Iteration 103/400, changed: 0.812217

---> Iteration 104/400, changed: 0.809437

---> Iteration 105/400, changed: 0.806724

---> Iteration 106/400, changed: 0.804076

---> Iteration 107/400, changed: 0.801480

---> Iteration 108/400, changed: 0.798937

---> Iteration 109/400, changed: 0.796448

---> Iteration 110/400, changed: 0.794008

---> Iteration 111/400, changed: 0.791612

---> Iteration 112/400, changed: 0.789282

---> Iteration 113/400, changed: 0.786984

---> Iteration 114/400, changed: 0.784728

---> Iteration 115/400, changed: 0.782516

---> Iteration 116/400, changed: 0.780355

---> Iteration 117/400, changed: 0.778216

---> Iteration 118/400, changed: 0.776139

---> Iteration 119/400, changed: 0.774087

---> Iteration 120/400, changed: 0.772072

---> Iteration 121/400, changed: 0.770085

---> Iteration 122/400, changed: 0.768146

---> Iteration 123/400, changed: 0.766232

---> Iteration 124/400, changed: 0.764356

---> Iteration 125/400, changed: 0.762504

---> Iteration 126/400, changed: 0.760685

---> Iteration 127/400, changed: 0.758889

---> Iteration 128/400, changed: 0.757135

---> Iteration 129/400, changed: 0.755406

四、LP算法MPI并行實現

這里，我們測試的是LP的變身版本。從公式，我們可以看到，第二項PULYL迭代過程并沒有發生變化，所以這部分實際上從迭代開始就可以計算好，從而避免重復計算。不過，不管怎樣，LP算法都要計算一個UxU的矩陣PUU和一個UxC矩陣FU的乘積。當我們的unlabeled數據非常多，而且類別也很多的時候，計算是很慢的，同時占用的內存量也非常大。另外，構造Graph需要計算兩兩的相似度，也是O(n2)的復雜度，當我們數據的特征維度很大的時候，這個計算量也是非常客觀的。所以我們就得考慮并行處理了。而且最好是能放到集群上并行。那如何并行呢?

對算法的并行化，一般分為兩種：數據并行和模型并行。

數據并行很好理解，就是將數據劃分，每個節點只處理一部分數據，例如我們構造圖的時候，計算每個數據的k近鄰。例如我們有1000個樣本和20個CPU節點，那么就平均分發，讓每個CPU節點計算50個樣本的k近鄰，然后最后再合并大家的結果。可見這個加速比也是非常可觀的。

模型并行一般發生在模型很大，無法放到單機的內存里面的時候。例如龐大的深度神經網絡訓練的時候，就需要把這個網絡切開，然后分別求解梯度，最后有個leader的節點來收集大家的梯度，再反饋給大家去更新。當然了，其中存在更細致和高效的工程處理方法。在我們的LP算法中，也是可以做模型并行的。假如我們的類別數C很大，把類別數切開，讓不同的CPU節點處理，實際上就相當于模型并行了。

那為啥不切大矩陣PUU，而是切小點的矩陣FU，因為大矩陣PUU沒法獨立分塊，并行的一個原則是處理必須是獨立的。 矩陣FU依賴的是所有的U，而把PUU切開分發到其他節點的時候，每次FU的更新都需要和其他的節點通信，這個通信的代價是很大的(實際上，很多并行系統沒法達到線性的加速度的瓶頸是通信!線性加速比是，我增加了n臺機器，速度就提升了n倍)。但是對類別C也就是矩陣FU切分，就不會有這個問題，因為他們的計算是獨立的。只是決定樣本的最終類別的時候，將所有的FU收集回來求max就可以了。

所以，在下面的代碼中，是同時包含了數據并行和模型并行的雛形的。另外，還值得一提的是，我們是迭代算法，那決定什么時候迭代算法停止?除了判斷收斂外，我們還可以讓每迭代幾步，就用測試label測試一次結果，看模型的整體訓練性能如何。特別是判斷訓練是否過擬合的時候非常有效。因此，代碼中包含了這部分內容。

好了，代碼終于來了。大家可以搞點大數據庫來測試，如果有MPI集群條件的話就更好了。

下面的代碼依賴numpy、scipy(用其稀疏矩陣加速計算)和mpi4py。其中mpi4py需要依賴openmpi和Cpython，可以參考我之前的博客進行安裝。

#***************************************************************************

#*

#* Description: label propagation

#* Author: Zou Xiaoyi (zouxy09@qq.com)

#* Date: 2015-10-15

#* HomePage: http://blog.csdn.net/zouxy09

#*

#**************************************************************************

import os, sys, time

import numpy as np

from scipy.sparse import csr_matrix, lil_matrix, eye

import operator

import cPickle as pickle

import mpi4py.MPI as MPI

#

# Global variables for MPI

#

# instance for invoking MPI related functions

comm = MPI.COMM_WORLD

# the node rank in the whole community

comm_rank = comm.Get_rank()

# the size of the whole community, i.e., the total number of working nodes in the MPI cluster

comm_size = comm.Get_size()

# load mnist dataset

def load_MNIST():

import gzip

f = gzip.open(mnist.pkl.gz, rb)

train, val, test = pickle.load(f)

f.close()

Mat_Label = train[0]

labels = train[1]

Mat_Unlabel = test[0]

groundtruth = test[1]

labels_id = [0, 1, 2, 3, 4, 5, 6, 7, 8, 9]

return Mat_Label, labels, labels_id, Mat_Unlabel, groundtruth

# return k neighbors index

def navie_knn(dataSet, query, k):

numSamples = dataSet.shape[0]

## step 1: calculate Euclidean distance

diff = np.tile(query, (numSamples, 1)) - dataSet

squaredDiff = diff ** 2

squaredDist = np.sum(squaredDiff, axis = 1) # sum is performed by row

## step 2: sort the distance

sortedDistIndices = np.argsort(squaredDist)

if k > len(sortedDistIndices):

k = len(sortedDistIndices)

return sortedDistIndices[0:k]

# build a big graph (normalized weight matrix)

# sparse U x (U + L) matrix

def buildSubGraph(Mat_Label, Mat_Unlabel, knn_num_neighbors):

num_unlabel_samples = Mat_Unlabel.shape[0]

data = []; indices = []; indptr = [0]

Mat_all = np.vstack((Mat_Label, Mat_Unlabel))

values = np.ones(knn_num_neighbors, np.float32) / knn_num_neighbors

for i in xrange(num_unlabel_samples):

k_neighbors = navie_knn(Mat_all, Mat_Unlabel[i, :], knn_num_neighbors)

indptr.append(np.int32(indptr[-1]) + knn_num_neighbors)

indices.extend(k_neighbors)

data.append(values)

return csr_matrix((np.hstack(data), indices, indptr))

# build a big graph (normalized weight matrix)

# sparse U x (U + L) matrix

def buildSubGraph_MPI(Mat_Label, Mat_Unlabel, knn_num_neighbors):

num_unlabel_samples = Mat_Unlabel.shape[0]

local_data = []; local_indices = []; local_indptr = [0]

Mat_all = np.vstack((Mat_Label, Mat_Unlabel))

values = np.ones(knn_num_neighbors, np.float32) / knn_num_neighbors

sample_offset = np.linspace(0, num_unlabel_samples, comm_size + 1).astype('int')

for i in range(sample_offset[comm_rank], sample_offset[comm_rank+1]):

k_neighbors = navie_knn(Mat_all, Mat_Unlabel[i, :], knn_num_neighbors)

local_indptr.append(np.int32(local_indptr[-1]) + knn_num_neighbors)

local_indices.extend(k_neighbors)

local_data.append(values)

data = np.hstack(comm.allgather(local_data))

indices = np.hstack(comm.allgather(local_indices))

indptr_tmp = comm.allgather(local_indptr)

indptr = []

for i in range(len(indptr_tmp)):

if i == 0:

indptr.extend(indptr_tmp[i])

else:

last_indptr = indptr[-1]

del(indptr[-1])

indptr.extend(indptr_tmp[i] + last_indptr)

return csr_matrix((np.hstack(data), indices, indptr), dtype = np.float32)

# label propagation

def run_label_propagation_sparse(knn_num_neighbors = 20, max_iter = 100, tol = 1e-4, test_per_iter = 1):

# load data and graph

print Processor %d/%d loading graph file... % (comm_rank, comm_size)

#Mat_Label, labels, Mat_Unlabel, groundtruth = loadFourBandData()

Mat_Label, labels, labels_id, Mat_Unlabel, unlabel_data_id = load_MNIST()

if comm_size > len(labels_id):

raise ValueError(Sorry, the processors must be less than the number of classes)

#affinity_matrix = buildSubGraph(Mat_Label, Mat_Unlabel, knn_num_neighbors)

affinity_matrix = buildSubGraph_MPI(Mat_Label, Mat_Unlabel, knn_num_neighbors)

# get some parameters

num_classes = len(labels_id)

num_label_samples = len(labels)

num_unlabel_samples = Mat_Unlabel.shape[0]

affinity_matrix_UL = affinity_matrix[:, 0:num_label_samples]

affinity_matrix_UU = affinity_matrix[:, num_label_samples:num_label_samples+num_unlabel_samples]

if comm_rank == 0:

print Have %d labeled images, %d unlabeled images and %d classes % (num_label_samples, num_unlabel_samples, num_classes)

# divide label_function_U and label_function_L to all processors

class_offset = np.linspace(0, num_classes, comm_size + 1).astype('int')

# initialize local label_function_U

local_start_class = class_offset[comm_rank]

local_num_classes = class_offset[comm_rank+1] - local_start_class

local_label_function_U = eye(num_unlabel_samples, local_num_classes, 0, np.float32, format='csr')

# initialize local label_function_L

local_label_function_L = lil_matrix((num_label_samples, local_num_classes), dtype = np.float32)

for i in xrange(num_label_samples):

class_off = int(labels[i]) - local_start_class

if class_off >= 0 and class_off local_num_classes:

local_label_function_L[i, class_off] = 1.0

local_label_function_L = local_label_function_L.tocsr()

local_label_info = affinity_matrix_UL.dot(local_label_function_L)

print Processor %d/%d has to process %d classes... % (comm_rank, comm_size, local_label_function_L.shape[1])

# start to propagation

iter = 1; changed = 100.0;

evaluation(num_unlabel_samples, local_start_class, local_label_function_U, unlabel_data_id, labels_id)

while True:

pre_label_function = local_label_function_U.copy()

# propagation

local_label_function_U = affinity_matrix_UU.dot(local_label_function_U) + local_label_info

# check converge

local_changed = abs(pre_label_function - local_label_function_U).sum()

changed = comm.reduce(local_changed, root = 0, op = MPI.SUM)

status = 'RUN'

test = False

if comm_rank == 0:

if iter % 1 == 0:

norm_changed = changed / (num_unlabel_samples * num_classes)

print ---> Iteration %d/%d, changed: %f % (iter, max_iter, norm_changed)

if iter >= max_iter or changed tol:

status = 'STOP'

print ************** Iteration over! ****************

if iter % test_per_iter == 0:

test = True

iter += 1

test = comm.bcast(test if comm_rank == 0 else None, root = 0)

status = comm.bcast(status if comm_rank == 0 else None, root = 0)

if status == 'STOP':

break

if test == True:

evaluation(num_unlabel_samples, local_start_class, local_label_function_U, unlabel_data_id, labels_id)

evaluation(num_unlabel_samples, local_start_class, local_label_function_U, unlabel_data_id, labels_id)

def evaluation(num_unlabel_samples, local_start_class, local_label_function_U, unlabel_data_id, labels_id):

# get local label with max score

if comm_rank == 0:

print Start to combine local result...

local_max_score = np.zeros((num_unlabel_samples, 1), np.float32)

local_max_label = np.zeros((num_unlabel_samples, 1), np.int32)

for i in xrange(num_unlabel_samples):

local_max_label[i, 0] = np.argmax(local_label_function_U.getrow(i).todense())

local_max_score[i, 0] = local_label_function_U[i, local_max_label[i, 0]]

local_max_label[i, 0] += local_start_class

# gather the results from all the processors

if comm_rank == 0:

print Start to gather results from all processors

all_max_label = np.hstack(comm.allgather(local_max_label))

all_max_score = np.hstack(comm.allgather(local_max_score))

# get terminate label of unlabeled data

if comm_rank == 0:

print Start to analysis the results...

right_predict_count = 0

for i in xrange(num_unlabel_samples):

if i % 1000 == 0:

print ***, all_max_score[i]

max_idx = np.argmax(all_max_score[i])

max_label = all_max_label[i, max_idx]

if int(unlabel_data_id[i]) == int(labels_id[max_label]):

right_predict_count += 1

accuracy = float(right_predict_count) * 100.0 / num_unlabel_samples

print Have %d samples, accuracy: %.3f%%! % (num_unlabel_samples, accuracy)

if __name__ == '__main__':

run_label_propagation_sparse(knn_num_neighbors = 20, max_iter = 30)