IIR數字濾波器的FPGA仿真與實現

數字濾波器是實現數字濾波的核心器件。常用的數字濾波器有FIR數字濾波器和IIR數字濾波器。文章介紹了一種基于EDA技術中的模塊化設計思想，采用VHDL硬件描述語言對IIR數字濾波器中的一些關鍵電路模塊進行設計,最終在FPGA上實現IIR 數字濾波器的方法[1]。

1 IIR數字濾波器硬件設計原理

1.1 數字濾波器的原理

數字濾波器的功能是完成信號濾波處理，是用有限精度算法實現離散時間線性非時變系統[2]。一個數字濾波器的系統函數H(z)可以表示為：
　　

　　直接由H(z)得出表示輸入輸出關系的常系數線性差分方程為：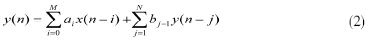


式中ai、bj-1為濾波系數，當bj-1均為零時，該濾波器為FIR數字濾波器，當bj-1不均為零時，則為IIR數字濾波器。

1.2 IIR數字濾波器的硬件實現方案比較

濾波器的實現主要包括兩大類：采用TMS320系列DSP芯片實現和采用PLD器件實現(主要包括FPGA和CPLD)。利用PLD器件實現時，可以采用硬件乘加模塊，從而使其運算速度比采用DSP器件快很多。因此基于FPGA的自編程實現方式成了濾波器實現的首選[3]。以下簡要介紹IIR數字濾波器的設計方案和基于FPGA的實現方法[4]。

方案一：直接相乘累加式

對于二階的IIR數字濾波器，其差分方程為：

　　因此可用5個硬件乘法器和4個硬件加法器來實現，采用這種方法對于高階的IIR數字濾波器的FPGA的設計來說是比較耗費資源的。

方案二：基于ROM查找表的VHDL結構化設計[5]

濾波器實現的主要任務是完成乘累加運算，采用ROM查找表方法可以避免使用硬件乘法器。由二階IIR濾波器的差分方程可以看出：yn僅取決于變量xn、xn-1、xn-2、yn-1和yn-2，因此可將a0、a1、a2、b0、b1的所有部分積存儲在ROM中，而以變量xn、xn-1、xn-2、yn-1和yn-2作為ROM的地址，從中選出對應的值，從而得到yn。

此方法避免了占主要運算量的乘法運算，節省了FPGA硬件資源，但使用不夠靈活。特別是當階數比較大時，更改ROM內的數據十分不便。

方案三：改進型設計

結合直接相乘累加式和ROM查表法的優點，用1個5路8位×1位的乘法器在8個時鐘周期內實現。其實現結構如圖1所示。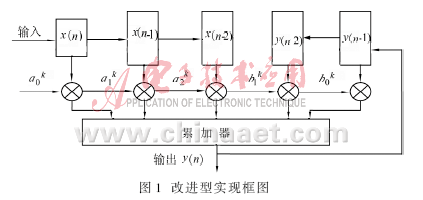

　　圖1中的X(n)與各自的系數的最高位相乘后，送入累加器相加后將和左移一位，以實現乘2運算。下一個時鐘，寄存器內數據與系數的次高位相乘，再送入累加器，然后再左移一位。接下來的6個時鐘進行類似的操作。第8個時鐘后，將累加器所得數據輸出即得到y(n)，對累加器清零，接著再進行下一次運算。

比較3種方案，方案三實現較為方便簡潔，在節省了FPGA硬件資源的同時，使得設計靈活，設計周期大為縮短，本設計即采用方案三來實現IIR數字濾波器。

2 IIR數字濾波器的具體實現和仿真

二階級聯法用于實現IIR數字濾波器硬件電路的應用是極為廣泛的，為此本文首先實現數字濾波器的二階節，然后用二階節的級聯實現更高階的濾波器。

2.1 IIR數字濾波器二階節的FPGA實現

IIR數字濾波器的二階節電路采用模塊化設計，把二階節分為延時模塊和補碼乘加模塊，其中補碼乘加模塊是設計的核心。

2.1.1 延遲模塊

延遲模塊功能是在clk時鐘作用下將差分方程的各x、y值延遲一個時鐘以實現一次延時運算，即當延時模塊輸入為x(n)和y(n)時，經過延時后輸出x(n)、x(n-1)、x(n-2)、y(n-1)和y(n-2) ,然后將輸出送到補碼乘加模塊運算。

2.1.2 補碼乘加模塊

補碼乘加模塊主要是用方案三的方法實現輸入序列{x(n)}、{y(n)}與系數ai、bi分別相乘后再相加的過程，即實現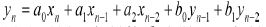。為了避免過多地使用乘法器，本設計中乘加單元(MAC)的乘法器采用陣列乘法器，以提高運算速度。

2.1.3 二階節的頂層模塊設計

頂層模塊設計采用原理圖輸入方法，將延遲模塊和補碼乘加模塊加入到系統中，并加入相應的輸入輸出引腳構成IIR濾波器的二階節。

2.1.4 二階節的系統仿真與結果分析

本次設計的二階節的輸入端x(n)寬為8位，可接8位AD轉換輸出的數據，輸出y(n)為16位數據。將實現的二階節在QuartusII中進行編譯綜合后，在波形圖中分別給定不同的濾波器系數和輸入不同的序列時，進行了波形仿真，這里給出其中的一個仿真波形如圖2所示(圖2是實現系統函數為：H(z)=(5+5z-1+5z-2)/(1-z-1-z-2) 的二階節的波形圖，其中a0、a1、a2、b0、b1為濾波器系數，xn為輸入序列，yn為輸出序列)。

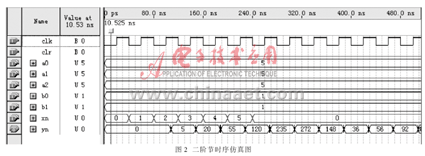
下面將對用FPGA實現的二階節時序波形仿真值和用Matlab對二階節的仿真結果相比較，分別對在輸入序列相同、但濾波器系數不同和濾波器系數相同、但輸入序列不同等幾種情況分別進行了比較，比較結果如表1所示。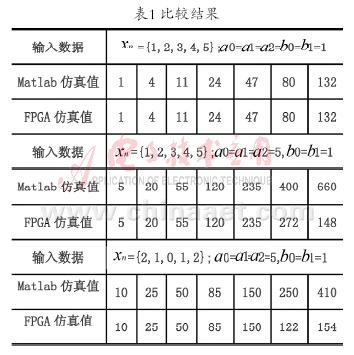

　　由表1可以看出所設計的二階節在不同系數和不同輸入情況下的FPGA仿真值和由Matlab計算值基本一致，說明采用方案三設計的二階節達到了設計要求。此外，表中仿真值與計算值有所偏差，而且隨著值的增大偏差越來越大，這是由于輸入位寬僅為8位的有限精度運算所引起的截斷誤差所致，要解決這一問題可以通過增加二進制位數來提高系統運算精度。

2.2 高階IIR數字濾波器的FPGA實現

要實現一個高階IIR數字濾波器，如果采用直接型結構實現，需要的乘法器和延遲單元相對較多，而且分子和分母的系數相差很大，因此需要較多的二進制位數才能實現相應的精度要求。而采用二階節級聯實現，一方面各基本節的零極點可以很方便地單獨進行調整，另一方面可以降低對二進制位數的要求，因此選用級聯結構。下面以四階IIR數字濾波器為例來說明高階濾波器的實現。

2.2.1 四階IIR濾波器的實現

四階IIR數字濾波器需要采用2個二階節級聯構成。其系統構成原理圖如圖3所示。圖中busconv模塊為總線轉換模塊，作用是將16位數據轉換為8位數據輸出。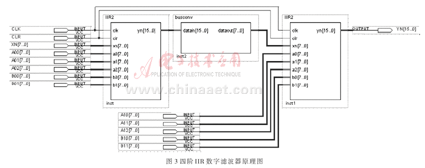


2.2.2 四階IIR濾波器的仿真波形和結果分析

四階濾波器輸入端x(n)寬為8位，輸出y(n)為16位數據。與二階節一樣將四階濾波器在QuartusII中進行編譯綜合并進行了時序波形仿真。在仿真中，設定的輸入序列xn為{1,2,3,4,5}，輸出為YN。第1個二階節IIR2(1)的系數為：A00=1,A01=2,A02=1,B00=1,B01=1,第2個二階節IIR2(2)系數為：A10=1,A11=1,A12=2,B10=1,B11=2，即實現的四階濾波器的系統函數為：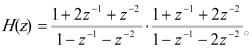


同樣將用FPGA實現的四階IIR濾波器時序仿真值與用Matlab仿真值進行了比較，如表2所示。因為采用二階節級聯，這里僅給出一組比較，其他情況與二階節相同。

　　由表2可見仿真結果與計算結果一致，且在不同的濾波器系數和不同輸入序列時所得出的結果與Matlab仿真值都一致，說明采用2個二階節級聯實現四階IIR數字濾波器達到了設計要求。同樣由于二階節存在有限精度引起的截斷誤差，四階濾波器也存在截斷誤差。

本文采用改進型方法在FPGA上成功實現了IIR數字濾波器，這種方法優點是不但減少了硬件乘法器的數量，節省了硬件資源，而且避免了系數發生變化時ROM中數據更改不方便的問題。缺點是在時間上付出了一定代價。在實際應用中可根據不同的階數、精度等要求，通過修改IIR數字濾波器外圍參數改變濾波器的頻率響應以實現任意階數濾波器，并且可以根據不同要求選擇在不同規模的FPGA上加以實現。