基于神經網絡的風電機組變槳距恒功率控制系統的研究

作者/ 黃俊梅 陜西能源職業技術學院電子工程系(陜西 咸陽 712000)

摘要：風力發電的開發對增加我國能源供應、調整能源結構具有重要意義。為了優化風電系統的穩定性，本文利用神經網絡在非線性建模方面的優越性，建立了一個基于神經網絡的風電機組變槳距恒功率控制系統。該系統在BP神經網絡變槳距模型的基礎上，利用SIMULINK工具箱搭建了風電機組變槳距恒功率控制系統模型。經仿真和實踐運行驗證，該模型控制效果良好，能根據風速檢測值調節槳距角，實現在不同風速段對發電機輸出功率的恒定控制，具有良好的穩定性和快速收斂性。

前言

　　伴隨著全球能源供應的環保化，風力發電作為一種清潔的可再生能源，有著取之不盡，用之不竭的優勢，擁有非常廣闊的市場前景^[1]。但風向、風速的隨機性所帶來的風力發電穩定性差是制約風力發電的瓶頸^[2]。為了克服這一技術難題，擁有智能、高效的風力發電變槳距恒功率控制系統顯得極其重要^[3]。

　　由于風力發電系統是一個非線性、強藕合、多變量、大時滯的系統，難以實現準確建模。而人工神經網絡技術不依賴于數學模型，可逼近任意非線性函數，具有較強的自適應、自學習和非線性映射能力，特別適應于復雜的風電變槳距控制系統建模^[4-5]。因此，本設計擬采用BP神經網絡進行風電機組變槳建模。在該BP變槳模型基礎上，利用MATLAB sumulink工具箱搭建風力發電變槳恒功率控制系統，并進行仿真驗證。為了進一步驗證本設計的合理性，將本BP變槳恒功率控制系統應用于山東長星風力發電機組，進行實驗驗證。

1 風力發電變槳恒功率控制系統

　　變槳距控制和恒功率控制是風力發電兩大核心技術^[6-7]。在風速低于額定風速時，為了最大限度跟蹤風速，此時沒有必要變槳，只需調整葉片槳距角為規定的最小槳矩角，即β=0°，使其風能利用系數最大。當風速超過額定風速時，系統輸出功率將會隨著風速的增高而不斷變大，這一過程對電網的穩定運行及設備安全有重要影響^[8-9]。因此，必須將輸出功率限制在額定范圍內。本設計將通過改變槳距角的大小，調整風能利用率，進而實現控制風輪轉速和保證風電機組恒功率輸出^[10-11]。

　　針對這一現象，本研究將主要針對額定風速以上的變槳恒功率控制系統進行建模仿真，其控制流程如圖1所示。

　　為了保證發電機組向電網提供平穩電能，本風力發電變槳恒功率控制系統采用功率閉環控制方式。其中，變槳控制器利用BP神經網絡建模實現。在此建模基礎上，利用MATLAB sumulink工具箱搭建風力發電變槳恒功率控制系統模型，將發電機輸出功率反饋到輸入端與額定功率進行比較，其偏差值作用于變槳控制器，最終使發電機的輸出功率穩定在額定值附近。

2 基于BP神經網絡的變槳距控制模型

2.1 BP神經網絡控制原理

　　BP神經網絡是一種按誤差逆傳播算法訓練的多層前饋網絡，其結構簡單、工作狀態穩定、易于硬件實現，是目前應用廣泛的神經網絡模型之一。

　　BP網絡能學習和存貯大量的輸入-輸出模式映射關系，而無需揭示描述這種映射關系的數學方程。通過反向傳播來不斷調整網絡的權值和閾值，使網絡的誤差平方和最小。BP神經網絡模型拓撲結構如圖2所示。

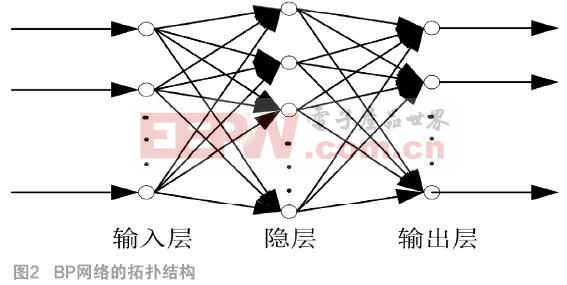
　　BP神經網絡通常由輸入層(input)、輸出層(output layer)和若干隱含層(hidden layer)構成。每層有若干個神經元組成，各神經元與下一層所有的神經元通過權連接，一個神經元可以處理多個輸入信息。BP神經網絡的自適應學習可歸納為 “信息正傳播”→“誤差逆傳播”→“記憶訓練”→“學習收斂”四個步驟。

　　信息正傳播：外界信息經由輸入層各神經元進入隱含層的神經元，并根據處理信息的復雜程度決定隱含層的層數，經隱含層和輸出層各神經元逐層信息處理后向外輸出信息結果。

　　誤差逆傳播：如果實際輸出與預期目標存在差異，則將誤差信息反向傳送，不斷記憶訓練修整權值大小，最終達到期望值為止，從而實現神經網絡的學習過程。

2.2 基于BP神經網絡的變槳距建模

　　一個BP神經網絡的建立通常包括網絡層數、各層神經元個數、學習速率、初始權值和允許誤差等參數。

　　1)BP模型網絡層數和各層神經元個數的確定

　　BP網絡一般包括1個輸入層，1個或幾個隱含層和1個輸出層。雖然增加層數可以提高精度、降低誤差，但這同時增加了網絡的復雜性和訓練時間。結合本研究實際，本建模將選用單隱層BP網絡進行仿真。

　　通過分析影響風電機組輸出功率的不同影響因素，最終確定輸入向量分別為風速，風輪角速度，輸出向量為變槳機構槳距角。利用試湊法，通過比較輸出誤差和收斂速度，最終確定隱層節點數為8。

　　2)傳遞函數的選擇

　　該BP模型的網絡的生成語句如下：

　　net=newff(minmax(pn),[8,1],{'tansig','purelin'},'trainlm')。其中，訓練選用trainlm函數，隱層選用tansig傳遞函數，輸出層選用purelin傳遞函數。

　　3)允許誤差和初始權值的設置

　　本文允許誤差設為0.005，初始權值選取(-1,1)之間的隨機數。

　　4) 學習速率的選擇

　　學習速率是優化計算中一個重要因子，反映網絡一次循環訓練中權值的變化量，取值范圍通常在0.01-0.8之間。取值太小將導致訓練時間過長，取值太大會導致系統不穩，因此本文中學習速率為0.05。

　　基于BP神經網絡的變槳距控制模型結構，如圖3所示。

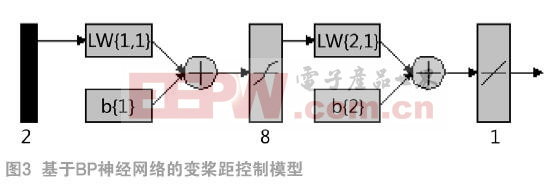
　　BP神經網絡變槳控制器模型建立之后，需要利用大量樣本數據進行模型的學習訓練。本文中的樣本數據來源于山東長星風力發電實驗室10kW風力機組的130組典型時段的樣本數據，選取前104組數據用于網絡訓練，后26組數據用于網絡的預測。

　　其中輸入樣本為各時段的風速、風輪角速度，輸出樣本為對應的槳距角。將訓練樣本數據做歸一化處理后再輸入神經網絡模型中進行訓練，得到網絡的閾值和權值;把預測數據經歸一化處理后，輸入到訓練好的神經網絡中，就可以計算輸出對應的槳距角值，如圖4所示。

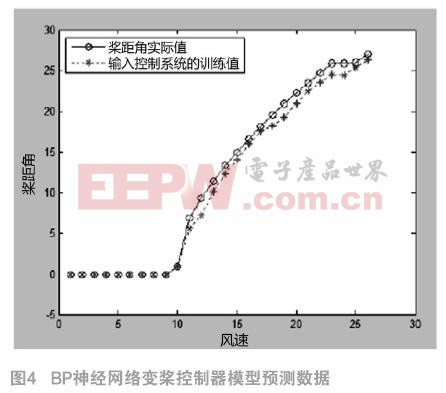
　　已知，該風電機組的額定風速為10.5m/s。從圖4可知，隨著風速的不斷變化，該BP模型的槳距角預測值可以很好地跟蹤實際值，預測效果較好。在額定風速以下時，槳距角為規定的最小槳矩角β=0°，可以最大限度地捕獲風能。當風速超過額定風速時，槳距角不斷增加，以期使風能利用率減小，從而將輸出功率限制在額定值附近。

3 風電機組變槳距恒功率控制系統模型仿真

3.1 風電機組變槳距恒功率控制系統模型仿真

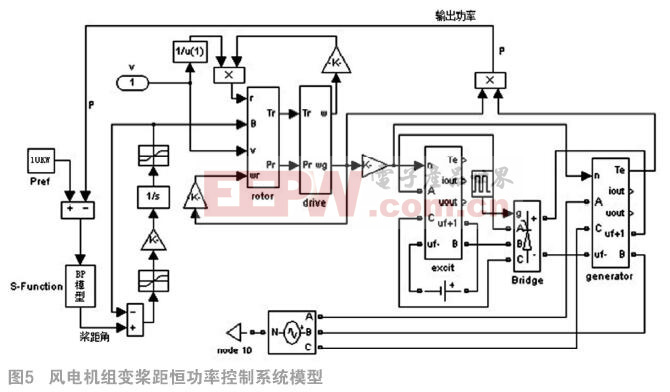
　　在已建好的BP神經網絡變槳距模型的基礎上，利用MATLAB仿真軟件的SIMULINK工具箱搭建風電機組變槳距恒功率控制系統模型，結構如圖5所示。

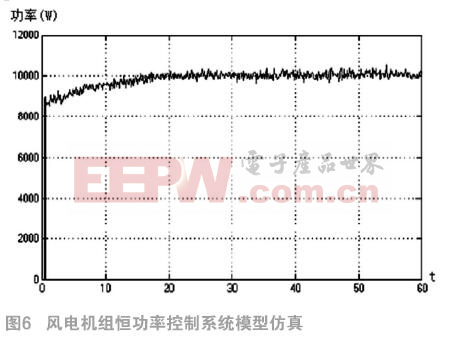
　　圖6為60s的隨機風速下，風電機組變槳距恒功率控制系統模型的輸出功率情況。由圖6可知，在60s的隨機風速下，本文所設計的風電機組變槳距恒功率控制系統模型可以很快實現額定功率10kW的穩定輸出，該系統具有很好的快速性和穩定性。

　　3.2 BP神經網絡變槳距模型的實際測試結果

　　為進一步驗證本變槳距恒功率控制系統在發電生產中的運行效果，將本模型嵌入至山東長星風力發電項目中，上機運行測試，測試結果如圖7所示。

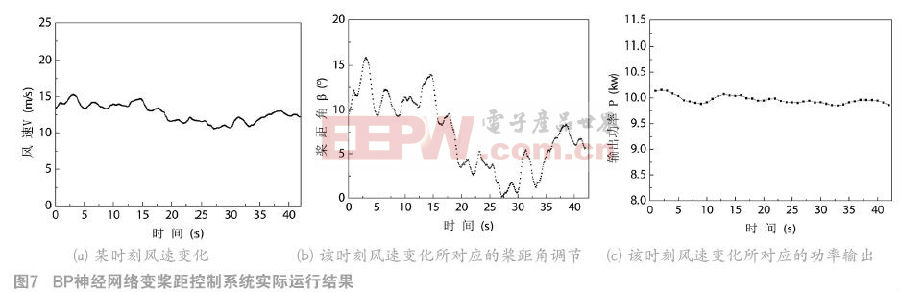
　　由圖7(a)和圖7(b)可知，在實際運行中槳距角隨著風速的變化而隨之自動調節。驗證了BP神經網絡變槳距控制系統發揮了控制作用。由圖7(c)可知，機組的輸出功率基本恒定于10kW，其上下波動屬于合理控制范圍內。圖7說明BP神經網絡變槳距控制系統，能夠通過改變葉片攻角而達到機組功率輸出恒定的目的，獲得理想的控制效果。

　　綜上所述，由于風電的強非線性，在不同風速下，槳距角的單位變化對發電機輸出功率影響不同。為保證額定功率為10kW的穩定輸出，在高風速段和額定風速附近，發生相同的風速變化△V，BP神經網絡變槳距控制系統通過槳距角的不同調節可以很快實現額定功率的穩定輸出。

4 結論

　　經仿真和實踐運行驗證，本文所設計的基于神經網絡的風電機組變槳距恒功率控制系統模型控制效果良好，能根據風速測定值調節槳距角，實現在不同風速段對發電機輸出功率的恒定控制，具有較好的穩定性和快速收斂性。

參考文獻：

　　[1]邊偉,謝毅.變槳矩風力發電機組輸出功率控制方法的應用研究[J].華北電力技術,2011,5.

　　[2]葉杭冶.風力發電機組的控制技術[M].北京:機械工業出版社,2002,81-95.

　　[3]杜志偉,趙峰,田銘興,等,變速恒頻風力發電的最大功率捕獲控制研究[J].電氣傳動,2007,37(3):7~10.

　　[4]呂躍剛,基于神經網絡的風力發電機組變槳距復合[J].2009,9(1) :28~34.

　　[5]崔冉,王維慶,趙春平,等.PID神經網絡在風機變槳控制中的應用[J].新疆:新疆大學,2008.

　　[6]張玉杰.基于IPC的風電機組智能控制與仿真技術研究[D].內蒙古科技大學,2014.6.

　　[7]張雅楠.變槳距與智能控制在風電機組中的應用,[J].沈陽:沈陽工業大學, 2010.

　　[8]薛永平.同步無刷風力發電機偏航變槳控制系統研究[D].陜西科技大學,2011.6.

　　[9]郭百順,秦斌,李鵬程.風電機組獨立變槳距控制策略研究[J].湖南工業大學學報,2014,28(2):42-45.

　　[10]許國東,潘東浩,葉杭冶.大型風電機組獨立變槳控制技術研究[J].太陽能學報,2011,32(6):891-896.

　　[11]邢作霞,陳雷,孫宏利,等.獨立變槳距控制策略研究[J].中國電機工程學報,2011,31(26):131-138.

　　本文來源于《電子產品世界》2017年第5期第76頁，歡迎您寫論文時引用，并注明出處。