輪轂盤式無鐵心永磁同步電機永磁體結構優化

作者 劉福貴 王彥剛 趙振興 劉慧敏 高春蘭  河北工業大學電磁場與電器可靠性省部共建重點實驗室(天津 300130)

*基金項目：天津市自然科學基金(編號：15JCYBJC16400)

劉福貴(1972-)，男，博士，教授，研究方向：電磁場與磁技術。

摘要：從優化永磁體結構的角度出發，提出將不等厚排列技術與90°Halbach陣列相結合方法對磁鋼的排列結構分析，通過改變磁鋼排列結構以進一步提高盤式無鐵心永磁同步電機(以下簡稱為DCPMSM)氣隙磁密的基波幅值及波形的正弦性，達到提高電機性能的目的。本文通過有限元仿真軟件對16極盤式永磁同步電機進行建模，分別選取不等厚排列電機模型、不等寬90°Halbach排列電機模型和改進型90°Halbach排列電機模型進行靜態氣隙磁場分析對比。仿真數據表明，“不等厚排列技術+90°Halbach陣列”使得周向磁密波形和切向磁密波形都大為改善，磁場波形更接近于正弦分布特征，其中周向磁密波形畸變率(THD)Bmin可降低到1.35%，氣隙周向磁密幅值Bδav提高到0.5465T。

引言

　　針對車用永磁同步電機高效率、高功率密度的要求，氣隙磁場的波形須為正弦波，幅值應足夠高，以電機磁場為優化目標進行分析^[1]。為確定電機磁場的優化變量，本文對其磁路進行定性分析，得到了影響磁場的主要因素是永磁體材料以及結構尺寸。因此，磁鋼尺寸成為磁場優化的關鍵。將不等厚原理應用于90°Halbach結構，能夠兼顧氣隙磁場的幅值與波形，對于提高電機功率密度、降低轉矩脈動^[2]等具有重要意義。并且利用盤式電機的設計原則對該特種電機的主要電磁參數進行了推導，對軸向磁場電機的后續設計提供了理論依據。

　　針對永磁同步電機對氣隙磁場^[3]的要求，提高電機的效率，降低電機的轉矩脈動^[4]及振動噪聲，電機磁場波形要接近正弦分布特性。為了兼顧以上要求，可以從電機永磁材料、磁鋼形狀和排列方式等方面考慮。永磁體選用磁性能優異的釹鐵硼材料。而對于磁鋼結構的研究，有文獻提出根據氣隙磁密波形設計不等厚磁鋼^[5-6]和采用不等厚磁鋼排列削弱氣隙磁密的諧波分量^[7]，但有很少文獻理論地介紹軸向充磁磁鋼的不等厚排列原理。有學者通過比較研究不同角度的Halbach陣列^[8]，得到最優的排列方式。90°Halbach陣列充磁較其他角度的方便^[9]、結構排列簡單、對工藝要求低^[10]，雖能夠滿足電機對氣隙磁密幅值的要求^[11]，但波形正弦性不夠理想。因此，提出將不等厚排列技術與90°Halbach陣列相結合方法對磁鋼的排列結構^[12]進行設計。

1 電機電磁參數與氣隙磁密的分析

　　氣隙磁密的基波幅值提高以及波形的正弦性對電機的各性能參數具有很重要的意義。當保持電機的主要尺寸不變時，通過對磁鋼的優化，提高電機氣隙磁密的基波幅值，使得電機的電磁轉矩和電磁功率得到提高;波形的正弦性對電機的空載反電動勢和轉矩脈動有很緊密的關系^[13]。

　　根據電機電磁參數與氣隙磁密的關系，氣隙磁密的基波幅值與電機的空載電動勢、電磁轉矩和電磁功率有緊密的關系。針對改善DCPMSM每極下的平均氣隙磁密的幅值和波形，目前有很多專家學者對電機的永磁體結構進行研究，其中，90°Halbach陣列技術和不等厚排列得到了很廣泛的應用，并且兩者相較普通磁鋼排列，平均氣隙磁密的幅值得到提高，正弦性也有顯著改善。因此，本文針對氣隙磁密的幅值及波形的正弦性，對電機的不等厚排列模型和不等寬90°Halbach陣列模型進行磁場仿真。

2 兩個電機模型的磁場仿真

2.1 不等厚排列電機模型的磁場仿真

　　每極有五塊不同厚度的磁鋼組成，中間磁鋼厚度由hm1表示，緊鄰的里側兩塊磁鋼厚度為hm2，最外側兩塊磁鋼厚度是hm3，且滿足h_m1>h_m2>h_m3。改變三塊磁鋼的厚度比可以得到幅值、波形均不同的氣隙磁場。

　　仿真結果顯示，改變h_m1時，B_δav與(THD)_B隨h_m2、h_m3的變化規律同h_m1=15mm的情況：每一個h_m1取值都有對應的(THD)_Bmin;B_δav隨h_m2減小同樣呈減小趨勢，即主要受hm₂影響。

　　由于受尺寸限制，hm₁=12mm對應的6.61%并不是(THD)B的極小值，而是仿真所取到的最小值，但并不影響最終結論。可見，隨hm₁的單調變化，(THD)_Bmin同樣先減后增，故存在最優情況，取(THD)_B值為1.70%，此時，B_δav=0.4615T，(hm₃,hm₂,hm₁)=(2,9,18)。

2.2 不等寬90°Halbach排列電機模型的磁場仿真

　　每極軸向充磁磁鋼與切向充磁磁鋼所占的幾何角度比值用k表示。不等寬與不等厚原理相同，都是改變磁鋼的磁化方向長度;前者針對切向充磁磁鋼，后者針對軸向充磁磁鋼。

　　波形幅值隨比值k的減小而增大，波形由馬鞍形波向尖頂波方向發展。減小比值k相當于增大切向充磁磁鋼的寬度，由仿真結果易知，增大切向充磁磁鋼所占的比例有利于增大磁密幅值，但波形質量也會變差;而增大k值，則相當于增大軸向充磁磁鋼的寬度，其極限情況即對應普通的N、S排列結構，因此波形會向馬鞍狀發展。因此，簡單地改變90°Halbach結構一極的寬度比，無法得到理想的效果。

3 改進型90°Halbach排列的電機模型磁場仿真

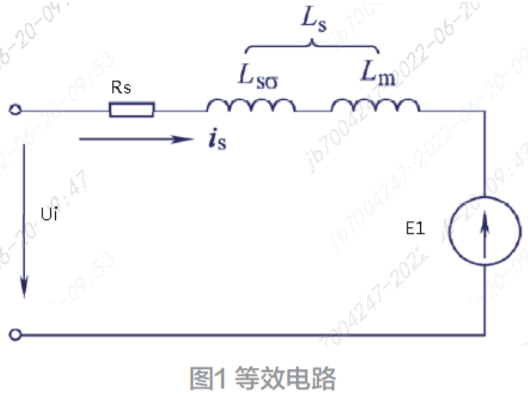
　　將軸向不等厚排列應用于90°Halbach陣列每極的兩塊磁鋼，其磁鋼平均半徑處的切向展開示意圖如圖1所示。即原有的每塊磁鋼變成三塊不同軸向厚度的磁鋼，中間厚度取為h1，對應的幾何角度所占比例為div1;兩邊厚度為h2，所占的比例均為div2。

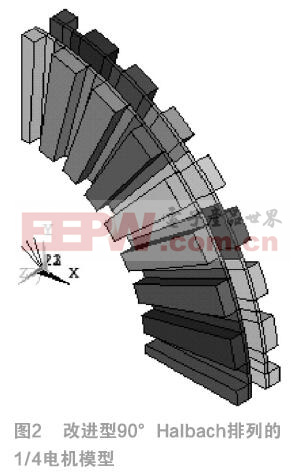
　　電機的四分之一仿真模型如圖2所示，是k取1前提下擁有最佳周向磁密波形的模型。該模型中，h₁=12mm，h₂=2.4mm，div₁=3.5/6。

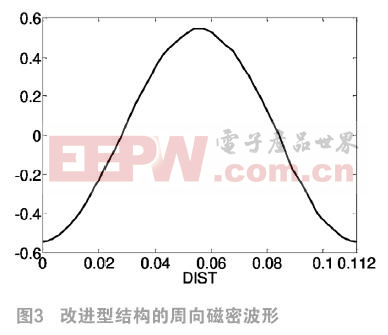
　　圖3顯示的是改進型電機的周向磁密波形，幅值為B_δav=0.5465T，且波形非常接近正弦波。與45°Halbach排列等結構相比，該模型雖然每極磁塊數增多，但在充磁方面仍然占優勢，且磁密波形也能達到要求。圖4所示的徑向磁密波形，相較90°Halbach基礎結構更加接近平頂波，永磁體內外徑間的磁場變化比較穩定。

　　令r=div₁/(2*div₂)，表示中間磁鋼與兩邊磁鋼所占幾何角的比值。具體優化過程：

　　(1)k=1。對于改進型的等寬結構，比較r變化時氣隙磁場的變化情況。首先對r=1時的電機模型進行仿真，此時div₁=2*div₂。改變h₁、h₂，分析氣隙周向、徑向磁場變化情況。

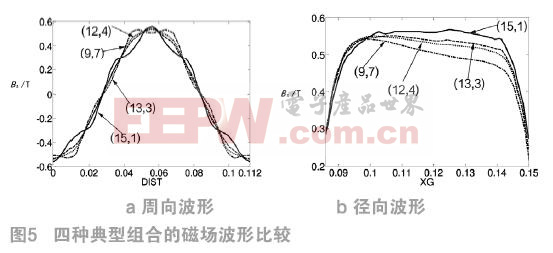
　　仿真結果表明，B_δav隨中間磁鋼的厚度h1的增大呈上升趨勢，(THD)_B則變化為先減小后增大，并在(h₁,h₂)取厚度組合(13,3)時獲得最小值;由周向波的變化趨勢就不難推斷波形質量最佳的情況必位于這組數據的中間某個組合;徑向波形以組合(12,4)為斜頂波與準平頂波的分水嶺，故(13,3)組合的徑向波形位于準平頂波之列。綜合分析，(13,3)是r=1時的最佳厚度組合。圖5比較了(h₁,h₂)取四種典型值的磁場波形。

　　對于r≠1的情況，取比值5:1~1:5之間的8種改進型結構模型進行仿真。結果顯示，(THD)_B及周、徑向波形隨組合(h₁,h₂)的變化規律基本同r=1情況：周、徑向波形變化趨勢大體一致;而對于某一特定的r值，對應的(THD)_B隨h₁增大的變化滿足先減小后增大的規律，(THD)B存在局部最優解(極小值)。但當r取5:1、4.5:1.5、1.5:4.5、1:5四種偏離1:1較遠的值時，在實際合理尺寸范圍內，(THD)_B并不存在極小值，處于發散狀態，且對準全局最優解(k=1時)不構成影響。

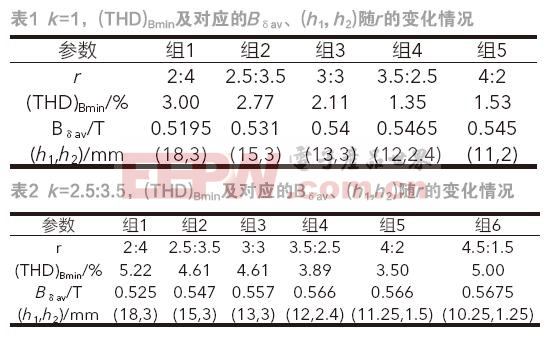
　　綜合比較r取不同值的(THD)_B極小值變化情況，結果總結列入表1。其中(THD)_Bmin表示周向磁密波形的THD極小值。(THD)Bmin隨r的增大先減小后增大，故k=1時，(THD)_B的準全局最優解存在，為1.35%，此時r=3.5:2.5，對應的(h₁,h₂)取(12,2.4)，B_δav為0.5465T。

　　(2)k≠1。對于改進型的不等寬結構，同樣令k取5:1~1:5之間的8個比值，仿真過程同上。對于k=2.5:3.5情況，仿真結果如表2所示。據前所述，最后一組數據并非仿真的最佳結果，而是考慮到實際尺寸限制所取的最小值。與表1比較，k取2.5:3.5時，r值對應的(THD)Bmin總體增大，但隨r的變化規律卻相同，且相應的厚度組合(h₁,h₂)也基本吻合。故k=2.5:3.5時，(THD)_B的準全局最優解存在，為3.50%，B_δav為0.566T。

　　由于k取其他七個比值時，周向磁場的仿真波形畸變率較嚴重，(THD)B的準全局最優解的情況更糟。對于其中任一種取值，r值所對應的(THD)B要么存在極值，但要明顯高于前述的兩種情況，要么發散、不存在極值。

4 結論

　　通過對90°Halbach結構^[14]的仿真，增加軸向充磁磁鋼的軸向厚度、將軸向充磁磁鋼劃分成不同厚度的若干塊小磁鋼或是增加切向充磁磁鋼所占的幾何角度等簡單地結合不等厚設計的諸多方法都無法得到高質量的波形。因此考慮對一對極的兩種充磁磁鋼都運用不等厚設計，將單塊的每種充磁磁鋼用三塊不等厚磁鋼代替。這樣雖然增加了每極磁鋼塊數，但周向磁密波形和切向磁密波形都大為改善，結果驗證了不等厚排列應用于90°Halbach結構的合理性，通過仿真數據顯示，(THD)B的最小值為1.35%，對應的k=1，r=3.5:2.5，(h1,h2)=(12,2.4)，Bδav為0.5465T。綜合考慮電機的實際情況，改進型90°Halbach電機采用周向磁密波形畸變率最小所對應的磁鋼結構，相對于90°Halbach型和不等厚型電機在氣隙磁密基波幅值和波形正弦性上都有所改善。

　　參考文獻：

[1]Nair S S,Nalakath S,Dhinagar S J.Design and analysis of axial flux permanent magnet BLDC motor for automotive applications[C].IEEE International Electric Machines & Drives Conference，2011:1615-1618.

　　[2]Aydin M, Gulec M.Reduction of Cogging Torque in Double-Rotor Axial-Flux Permanent-Magnet Disk Motors: A Review of Cost-Effective Magnet-Skewing Techniques With Experimental Verification[J].IEEE Transactions on Industrial Electronics，2014,61(9): 5025-5034.

　　[3]Li J G,Wu D Y,Zhang X D.A new permanent-magnet vernier in-wheel motor for electic vehicles [C].Proceedings of IEEE Vehicle Power and Propulsion Conference，2010.

　　[4]Huang C C,Li P L,Chuang F C,et al.Optimization for Reduction of Torque Ripple in an Axial Flux Permanent Magnet Machine[J].IEEE Transactions on Magnetics，2009,45(3):1760-1763.

　　[5]方淑丹.永磁直流電動機不等厚瓦形磁鋼的設計[J].微特電機,1999(1):15-18.

　　[6]劉超,孫立志,孫立.永磁同步伺服電動機氣隙磁場優化設計[J].微電機,2010,43(11):24-26.

　　[7]金友華,王宏偉.基于Ansoft優化永磁同步電機氣隙磁密[J].微電機，2013,46(12)：24-26.

　　[8]孫程英.不同結構永磁同步電機的磁場分析[D].北京:華北電力大學,2008.

　　[9]閆杰.盤式無鐵心永磁同步電機磁場分析及磁鋼結構優化[D].天津:天津大學,2004.

　　[10]Bumby J R,Martin R.Axial-flux permanent-magnetair-cored generator for small-scale wind turbines[J].Proc.IEEE Proceedings-Electric Power Applicatio-ns，2005,152(5):1065-1075.

　　[11]李桂丹,于海峰,王曉遠,等.基于Halbach陣列的盤式無鐵心永磁同步電機磁鋼優化[J].微電機,2015,48(2):1-6.

　　[12]謝龍漢,耿煜,邱婉.ANSYS電磁場分析[M].北京:電子工業出版社,2012.

　　[13] Giulii Capponi F,De Donato G,Caricchi F.Recent Advances in Axial-Flux Permanent-Magnet Machine Technology[J].IEEE Transactions on Industry Applications，2012,48(6):2190-2205.

　　本文來源于《電子產品世界》2017年第4期第33頁，歡迎您寫論文時引用，并注明出處。