生物電阻抗測量系統中弱信號檢測技術研究--EIT 中弱信號檢測理論

檢測中的電噪聲主要是由檢測系統內部噪聲引起，由電阻和各種器件產生的。絕大多數的電噪聲是一個連續型隨機變量，是一種前后獨立的平穩隨機過程，在任何時刻，它的幅度、相位以及波形都是隨機的，但還是服從于一定的統計分布規律。

電阻熱噪聲是由電阻內部自由電子的熱運動而產生的。起伏電流，電阻中的帶電微粒(自由電子)在一定溫度下受到熱激發后，在導體內部作無規則的運動(熱騷動)而相互碰撞，兩次碰撞之間進行時，就產生一持續時間很短的脈沖電流。許多這樣的隨機熱騷動電子所產生的這種脈沖電流組合，就在電阻內部形成了無規律的電流。在一足夠長的時間內，其電流的平均值等于零，而瞬時值就在平均值上下變動。當實際電路中包含多個電阻時，每一個電阻都將引入一個噪聲源。一般若有多個電阻并聯時，總噪聲電流等于各個電導所產生的噪聲電流的均方值相加。

2.3常用弱信號檢測算法

生物弱信號的特點是幅度小，往往淹沒在噪聲之中。為了檢測被背景噪聲覆蓋的微弱信號，人們進行了長期的研究工作，分析噪聲產生原因及規律，研究被測信號的特點、相關性及噪聲的統計特性，以尋找從背景噪聲中檢測出有用信號的方法。常用的微弱信號檢測方法有：相干檢測法、基于混沌振子的微弱信號檢測、同步累積法、雙路消噪法、窄帶濾波法等。

2.3.1相干檢測法

相關接收技術是應用信號周期性和噪聲隨機性的特點，通過自相關或互相關運算，達到去除噪聲、檢測出信號的一種技術[13][15]。由于信號和噪聲是相互獨立的過程，根據相關函數和互相關函數定義，信號只與信號本身相關，與噪聲不相關，而噪聲之間一般也不相關。

2.3.1.1自相關檢測

實現自相關檢測的原理框圖[13]如圖2.3所示。

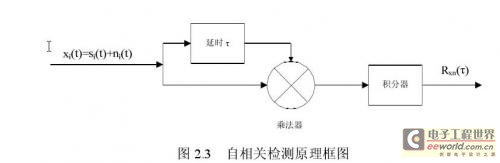
設輸入x i(t)由被測信號s i(t)和噪聲n i(t)組成，即：

x i(t)同時輸入到相關接收機兩個通道，其中一路將經過延時器，使它遲延一段時間τ。經過遲延的x i(t-τ)和未經遲延的x i(t)均送入乘法器內，再將其乘積積分，然后輸出平均值，從而得到相關函數上一點的相關值。如果變更遲延時間τ，重復上述計算就能得到相關函數R xx(τ)與τ的關系曲線，即得自相關的輸出為：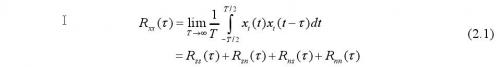

根據互相關函數性質，由于信號s(t)與噪聲n(t)不相關，并且噪聲的平均值為零，得到R sn(τ)=0，R ns(τ)=0，則R xx(τ)= R ss(τ) +R nn(τ)。隨著τ的增大，R nn(τ)→0，則對充分大的τ，可得R xx(τ)= R ss(τ)。這樣就得到了信號s i(t)的自相關函數R xx(τ)，它將包含著s i(t)所攜帶的某些信息。

隨著時間τ的增加，噪聲的自相關函數迅速衰減，而信號的自相關函數是小衰減的周期函數，從而可檢測出有用信號。

2.3.1.2互相關檢測

如果發送信號的重復周期或頻率已知，就可在接收端發出一路重復周期與發送信號相同的本地信號，將本地信號與混有噪聲的輸入信號進行互相關。如圖2.4是實現互相關檢測的原理框圖，設輸入x(t)為：x (t ) = s (t ) +n (t )

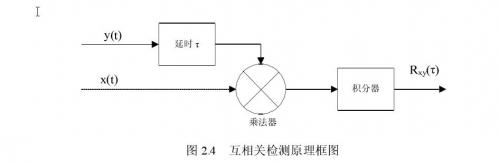
s(t)為待測信號，n(t)為信號s(t)中混入的噪聲，y(t)為己知參考信號，若y(t)與信號s(t)有相關性，而與噪聲n(t)無相關性，輸入經延時、相乘、積分及平均運算后，得到互相關輸出R xy(τ)為：

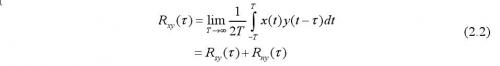
由于參考信號y(t)與信號s(t)有某種相關性，而y(t)與噪聲n(t)沒有相關性，且噪聲的平均值為零，則有R ny(τ)=0，即：

根據互相關函數的性質R xy(τ)中包含了信號s(t)所攜帶的信號，從而將待測的信號s(t)檢測出來。

2.3.2基于混沌振子的微弱信號檢測

混沌理論作為一門新學科已經引起了大家的重視，是近年來非線性科學領域的熱門學科。混沌目前尚無通用、嚴格的定義，一般認為，在某些確定性非線性系統中，不需要附加任何隨機因素，僅由其內部存在著非線性的相互作用所產生的類隨機現象稱為混沌。當系統發生混沌行為時，系統響應對系統參數由噪聲產生的攝動并不敏感，也就是系統的混沌行為對噪聲具有一定的免疫力，這類非線性系統行為對參數的依賴性和混沌吸引子對噪聲的免疫力使其在微弱特征信號檢測方面具有潛在的應用前景。在許多工程實際中，微弱特征信號的產生就表明系統的運行狀態發生了變化，如何檢測這些在強噪聲干擾情況下的微弱信號是信號處理中的重要研究內容。

目前混沌振子用于微弱信號檢測的研究己經越來越深入。混沌振子由于參數的不同會表現出不動點、周期、擬周期、混沌等動力學狀態。對兩種狀態的相互轉換時的參數臨界值，在非線性科學中稱為“分叉值”，兩種狀態間的轉換稱為“分叉”。Duffing振子信號檢測技術主要是利用混沌系統的分岔特性來檢測外界信號，將待測信號作為Duffing方程周期策動力的攝動，利用初值敏感性可以獲得很高的測量靈敏度和良好的抗噪性能。

利用混沌振子檢測微弱信號的方法就是將一個非線性含參數系統設定在其參數的臨界值附近，微弱的特征信號作為對分叉參數的攝動，當具有某一微弱的特征信號作為攝動項加入系統時，則非線性系統的定性狀態就會發生變化。通過對非線性系統的定性狀態有無發生變化進行判別，進而達到檢測微弱特征信號的目的。

由混沌理論知：一類混沌系統在一定條件下對小信號具有敏感性，同時對噪聲具有免疫力，因此使得它在信號檢測中非常具有潛力。由非線性理論知：對于一個非線性系統，當其敏感參數在一定范圍存在攝動時，將引起其周期解發生本質變化。由此，可以利用非線性系統的周期解所發生的本質變化來檢測微弱信號。

當采用Duffing振子作為非線性系統來檢測微弱信號時，讓Duffing振子處于混沌和周期解之間的臨界狀態，將待測信號作為Duffing振子周期策動力的攝動，通過Duffing振子對噪聲和目標信號的不同反應來檢測目標信號。當待測信號經過Duffing振子時，噪聲雖然強烈，辯識系統狀態，可以清楚地檢測出特定信號是否存在。

利用混沌振子方法可以從很強的噪聲信號中檢測其中的特征信號是否存在，該方法具有巨大的應用潛力。但這種方法也存在一定的缺陷：

1.若系統輸出本來就是穩定周期狀態，但由于無法事先知道，所以只能通過觀察相圖，最終證明輸出是穩定狀態，那么這種判別方法的工作效率是比較低的。

2.根據系統的相軌跡圖來判別系統的狀態，即系統是處于混沌狀態還是已經躍變到了周期狀態，也是不夠準確的，容易出現誤判。這種判別方法雖然簡單、直觀，但終歸是一種人為的識別方法，所以沒有一個嚴格意義下的數學判別標準，缺乏理論依據。

2.3.3同步積累法

同步積累法的原理是利用信號的重復性和噪聲的隨機性，對信號重復測量多次，使信號同相的積累起來。噪聲則無法同相積累，使信噪比得到改善。在這種方法中，測量次數越多，則信噪比改善越明顯。

若測量次數為n，則積累的信號為：

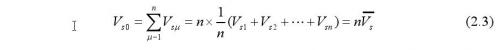
其中，

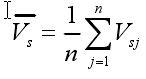
為累積信號的平均值，實際上等于輸入信號V si。另一方面，重復測量n次后，根據各次噪聲的不相關性，則積累的噪聲等于：

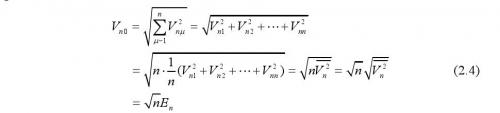
上式中最后的E n為累積噪聲的均方根值。

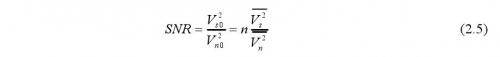
得到信噪比為：因此，測量次數n越大，則信噪比的改善越明顯。而增加測量次數，就意味著延長測量時間，所以信噪比的改善是以耗時間換來的。