PMMA塑料車窗升降運動偏差仿真與試驗分析
加入技術交流群
國內外有很多研究人員對雙曲面玻璃及其升降導軌進行了較為深入的研究， 其中包括：同濟大學的高云凱教授、同濟同捷科技股份有限公司的雷雨成教授等采用圓環面方法擬合雙曲面玻璃；并且利用UG 等軟件實現了圓環面玻璃的幾何設計和運動偏差分析。福特公司的Singh 等人借助CAE 分析方法研究了車門玻璃在升降運動過程中的偏差以及密封條變形。但是研究人員主要在雙曲面車門玻璃升降導軌設計和仿真偏差方面取得一定成績，但是少有人通過試驗方法測量玻璃升降運動的偏差，而試驗驗證始終是檢驗理論設計的有效方法。試驗不僅可以考慮車門的生產、制造偏差，導槽密封條的作用，這些是仿真中沒有考慮的，還可以檢驗仿真中導軌設計的有效性。
因此，本文提出了一種測量計算雙曲面玻璃運動偏差的試驗方。同時還提出了一種擬合圓環面的方法，這種方法比文獻中的嘗試法更加精確。用仿真和試驗的方法研究了PMMA 側窗的升降運動偏差性能。結果表明，PMMA 玻璃仿真與試驗的趨勢一致，因此驗證了仿真中導軌設計的有效的；而PMMA 的運動偏差小于無機玻璃，說明PMMA 的升降運動偏差性能優于無機玻璃。
1 玻璃升降運動偏差仿真分析
1.1 擬合升降導軌
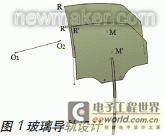
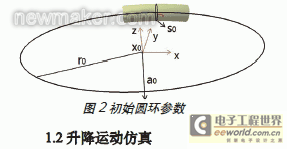
以上海某設計公司的一款A 級車左后門為研究對象， 針對其雙曲面車門玻璃的幾何模型， 采用比例函數法擬合其升降導軌導線及導槽導線。根據玻璃圓環面的運動理論可知：理想情況下，即玻璃曲面不存在運動偏差時，玻璃曲面在下降過程中，R 點一定經過R’’點。所以， 車門玻璃下降的過程中，初始位置上的R 點繞軸線O1O2 旋轉到R’點，然后再沿軸線O1O2 方向偏移到R’’點，如圖1 所示。那么玻璃質心M 點沿同樣的圓環面運動時，點M 的運動軌跡即為玻璃導軌的導線，設計結果如圖2 所示。
調用DMU Kinematic 模塊進行玻璃升降運動仿真，分別測量玻璃在上止點位置、中間位置及下止點位置時玻璃坐標。
1.3 圓環法擬合玻璃形面
論文在UG 中選取玻璃上的點，通過嘗試法擬合的圓環較為粗糙，不能精準確定玻璃型面的位置，因此本文提出一種用圓環法擬合玻璃型面的方法，在matlab 軟件中，運用坐標變換和最小二乘的方法較為精確地擬合了圓環面，根據測得的窗框上點的坐標，運用Matlab 軟件根據最小二乘法擬合圓環面， 將此圓環面作為玻璃型面，計算玻璃升降運動后距離圓環面的偏差作為玻璃升降運動偏差。
（1）選取擬合圓環初始值：
仿真時需要輸入的參數為窗框上點的坐標和圓環面的初始參數。其中，圓環初始參數包括：大圓環圓心（X0，Y0， Z0），大圓環的軸線向量
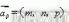，大圓環的半徑r0，小圓環的半徑s0。如圖2 所示，在Catia 中輸入窗框的坐標，通過窗框上邊緣距離較遠的三點確定大圓環， 量取大圓環的圓心、軸線和半徑，然后在窗框靠近B 柱的邊緣距離較遠的三點確定小圓環，量取小圓環的半徑。 二窗框點的坐標集記為X，其中i 點的坐標為
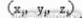。 （2）旋轉坐標
由大圓環軸線得到旋轉角θ1和θ2，sinθ1、cosθ1、sinθ2和cosθ2可表示為公式（1-4）。通過旋轉平移將窗框上的點旋轉到以大圓環圓心為原點，Z 軸與圓環軸線相重合的坐標系中。設旋轉后窗框上點坐標集為X2，i 點的坐標變為
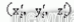，則旋轉后的坐標如公式（3） 所示。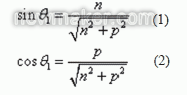 
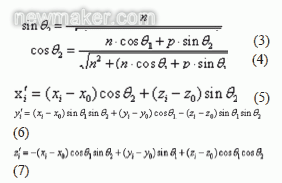
根據公式（8）計算旋轉后窗框上點i 到圓環面的距離 ，用最小二乘法求得偏差最小條件下的圓環參數，如公式（9） 所示。
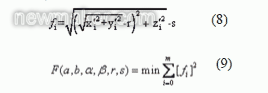
最后，通過旋轉平移得到在原坐標系下的圓環面參數：x0n=（15633，560，- 22182），an=（8359，55，5489）， rn=26395，sn=1168.2。
1.4 計算運動偏差
當玻璃運動到不同位置時， 計算玻璃上樣本點距離圓環面的距離， 得到玻璃的升降運動偏差， 其分析結果如圖3 所示。
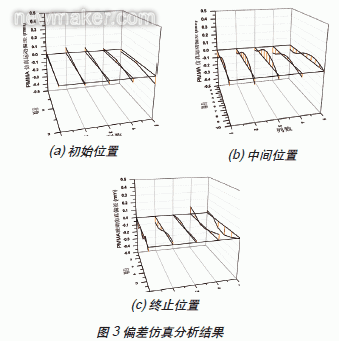
2.1 試驗環境與設備
試驗主要采用HXY 系列單臂三維測量劃線儀，也就是三坐標測量儀。試驗環境溫度： 30℃ -32℃。玻璃運動偏差試驗驗證裝置如圖6 所示。
評論