數字PID控制及其改進算法的應用
2 PID控制的改進算法
在理想的數學模型中加入大小為-0.25~0.25的Dead Zone(死區),如圖3所示進行仿真,仿真實驗結果如圖4所示。仿真中為了更好的探討積分環節的作用,取KD=0。圖中Kp=3,實線無積分控制作用,可以看出有較大靜差;點線為加入積分控制,并取KI=0.0015;分析可知:積分環節可以減小上升時間,但會增大超調量,延長調整時間。事實上,如果要減小上升時間,可以增大Kp的值,沒有必要為了減小上升時間而加大KI的值。
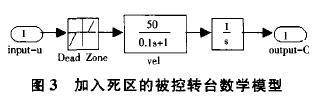
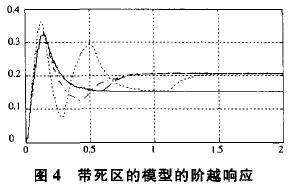
圖4中虛線為采用積分分離PID控制的過程,可以看出積分分離PID算法明顯改善了控制過程。積分分離PID算法的思想是在誤差較小時保留積分控制作用,而在誤差較大時取消積分控制環節。積分分離PID控制器在誤差較大時保證系統的跟蹤性能,而在誤差較小則能保證系統穩態精度和抗干擾性能,較大的改善控制性能。
積分分離PID控制寫成公式時,可在積分項乘一系數β,其值根據誤差大小來決定。

其中:ε>0——設定的閾值。此時積分分離PID控制算式的積分控制寫為:

積分分離PID算法的另一本質就是改變了過去的誤差對控制量的權系數,而不再是普通的求和(普通的求和權系數相同,都是1)。同時我們可以用連續函數(連續或分段連續)來計算求和的權重,比如采用連續函數:
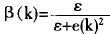
來計算權系數β(k),其中參數ε根據需要調整,當e(k)2=ε時,β(k)=0.5。此時,積分控制量寫為:
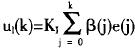
圖4中的點畫線為變速積分控制過程,其中ε=0.0015,KI=0.004。顯然變速積分法要比積分分離算法效果要好,但是變速積分法要花費更大的代價來實現,而且積分分離算法效果不錯,變速積分法只不過稍稍改善了一些性能。
根據各種改進積分環節算法的有效性和代價,我們選擇容易實現而且效果不錯的積分分離算法運用于我們實際的轉臺控制,得到了很好的控制效果。
3 結束語
根據對轉臺控制的仿真和經驗,總結出PID參數工程整定的一般步驟:
只加入比例控制環節,慢慢增加Kp使系統微微振蕩起來;
加入微分控制環節,慢慢增加KD,這相當于增大系統的阻尼,使系統平穩下來;
系統平穩下來后,再增加Kp使系統微微振蕩起來,然后再增加KD使系統平穩下來,如此反復下去,直到Kp和KD都不能增加時為止;
再把Kp的值適當減小一點。加入積分控制環節,慢慢增加KI的值,直到穩態誤差在可接受的范圍內;⑤ 為了使系統更可靠和穩定,保證魯棒性。最后還要把KP、KD、KI的值都適當減小,再根據經驗做一些相應的調整。



評論