硬件設計：

總體思路：

整個機架采用PCB板，將四個電機固定在PCB板的四個角，外接電池。

硬件模塊：

單片機、慣性測量模塊(IMU)、無線通訊模塊、電機驅動模塊、續流二極管、電源管理模塊(穩壓與充放電)、直流有刷電機、大電流放電電池、遙控器。

硬件選型：

硬件工作綜述：

單片機負責整個系統的協調工作；慣性測量模塊(IMU)負責測量四旋翼的姿態；無線通訊模塊負責四旋翼與遙控器的通訊；電機驅動模塊負責驅動電機；續流二極管負責對電機進行續流；電源管理模塊中的穩壓模塊負責整個系統的供電，電源管理模塊中的充放電模塊負責對電池充電；有刷電機負責提供四旋翼的飛行動力；大電流放電電池負責四旋翼的能量來源；遙控器負責對四旋翼進行遙控和控制。

硬件設計功能模塊圖：

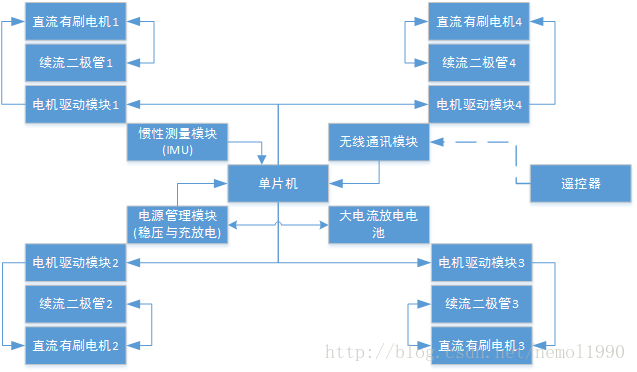
實際效果圖與相關參數：

尺寸：對角電機軸距10x10cm

重量：33.2g(帶電池)

軟件設計：

總體思路：

慣性測量模塊(IMU)測量出當前飛機的三軸加速度與三軸角速度并傳送給單片機處理，由單片機進行基于四元數的姿態解算，求解出當前飛機的pitch、roll、yaw三個角度值，然后根據這三個角度經過PID控制運算，輸出四路PWM控制四個直流有刷電機的加減速從而達到飛機的平衡懸停。

其中，慣性測量模塊(IMU)的加速度計由于噪聲比較大，所以需要對其進行濾波處理；而遙控器則是對飛機進行實時的姿態控制；最后由于四旋翼制作的特殊性，在調試PID參數階段會頻繁的燒寫程序，鑒于此，筆者開發了基于NRF24L01的Bootloader技術，免除了燒寫Flash的物理連線限制，可實現遠程程序一鍵下載。

姿態解算：

姿態解算屬于四旋翼制作的核心部分，如果姿態解算能夠實時的反應出飛機的狀態，那么對于控制來講就相對來說比較容易了。而姿態結算所要做的事情就是兩個坐標系之間的正確轉化(地理坐標系與載體坐標系)，這種轉化有很多種表示方法，例如歐拉角法、方向余弦矩陣法、四元數法、旋轉矢量法等。筆者采用的是應用廣泛的四元數法，而旋轉矢量法則是一種基于四元數法的改進四元數法。

四元數本是用于描述四維空間向量的一種方法，對于他的線性變換也就是在四維空間中的拉伸和旋轉，顯而易見，我們用四元數的向量乘法來表示三維空間中的旋轉是綽綽有余的。

通過慣性測量模塊(IMU)傳送過來的當前飛機的三軸加速度和三軸角速度的值，這樣一個三維的向量，轉化為四維向量，然后在四維空間中做線性變換(也可以說在三維空間中旋轉)后輸出，利用四元數與歐拉角的關系(一定要注意旋轉順序)，將當前四元數轉換為歐拉角pitch、roll、yaw即得到當前飛機的姿態。

以下給出筆者姿態融合的代碼，該代碼網上都有，筆者在這里做了些許注釋，方便理解。

[cpp]view plaincopyprint?

2. voidIMUupdata(floatgx,floatgy,floatgz,floatax,floatay,floataz)
3. {
4. floatrecipNorm;//平方根的倒數
5. floathalfvx,halfvy,halfvz;//在當前載體坐標系中，重力分量在三個軸上的分量
6. floathalfex,halfey,halfez;//當前加速度計測得的重力加速度在三個軸上的分量與當前姿態在三個軸上的重力分量的誤差,這里采用差積的方式
7. floatqa,qb,qc;
9. gx=gx*PI/180;//轉換為弧度制
10. gy=gy*PI/180;
11. gz=gz*PI/180;
13. //如果加速度計處于自由落體狀態，可能會出現這種情況，不進行姿態解算，因為會產生分母無窮大的情況
14. if(!((ax==0.0f)&&(ay==0.0f)&&(az==0.0f)))
15. {
16. //單位化加速度計,意義在于在變更了加速度計的量程之后不需要修改Kp參數,因為這里歸一化了
17. recipNorm=invSqrt(ax*ax+ay*ay+az*az);
18. ax*=recipNorm;
19. ay*=recipNorm;
20. az*=recipNorm;
22. //將當前姿態的重力在三個軸上的分量分離出來
23. //就是方向余弦旋轉矩陣的第三列,注意是地理坐標系(n系)到載體坐標系(b系)的,不要弄反了.如果書上是b系到n系,轉置即可
24. //慣性測量器件測量的都是關于b系的值，為了方便，我們一般將b系轉換到n系進行導航參數求解。但是這里并不需要這樣做，因為這里是對陀螺儀進行補償
25. halfvx=g_q1*g_q3-g_q0*g_q2;
26. halfvy=g_q0*g_q1+g_q2*g_q3;
27. halfvz=g_q0*g_q0-0.5f+g_q3*g_q3;
29. //計算由當前姿態的重力在三個軸上的分量與加速度計測得的重力在三個軸上的分量的差,這里采用三維空間的差積(向量積)方法求差
30. //計算公式由矩陣運算推導而來公式參見http://en.wikipedia.org/wiki/Cross_product中的Mnemonic部分
31. halfex=(ay*halfvz-az*halfvy);
32. halfey=(az*halfvx-ax*halfvz);
33. halfez=(ax*halfvy-ay*halfvx);
35. //積分求誤差,關于當前姿態分離出的重力分量與當前加速度計測得的重力分量的差值進行積分消除誤差
36. if(g_twoKi>0.0f)
37. {
38. g_integralFBx+=g_twoKi*halfex*CNTLCYCLE;//Ki積分
39. g_integralFBy+=g_twoKi*halfey*CNTLCYCLE;
40. g_integralFBz+=g_twoKi*halfez*CNTLCYCLE;
41. gx+=g_integralFBx;//將積分誤差反饋到陀螺儀上，修正陀螺儀的值
42. gy+=g_integralFBy;
43. gz+=g_integralFBz;
44. }
45. else//不進行積分運算，只進行比例調節
46. {
47. g_integralFBx=0.0f;
48. g_integralFBy=0.0f;
49. g_integralFBz=0.0f;
50. }
52. //直接應用比例調節，修正陀螺儀的值
53. gx+=g_twoKp*halfex;
54. gy+=g_twoKp*halfey;
55. gz+=g_twoKp*halfez;
56. }
58. //以下為四元數微分方程.將陀螺儀和四元數結合起來，是姿態更新的核心算子
59. //計算方法由矩陣運算推導而來
60. //.1
61. //q=-*qxOmega式中左邊是四元數的倒數,右邊的x是四元數乘法,Omega是陀螺儀的值(即角速度)
62. //2
63. //.
64. //[q0][0-wx-wy-wz][q0]
65. //.
66. //[q1][wx0wz-wy][q1]
67. //.=*
68. //[q2][wy-wz0wx][q2]
69. //.
70. //[q3][wzwy-wx0][q3]
71. gx*=(0.5f*CNTLCYCLE);
72. gy*=(0.5f*CNTLCYCLE);
73. gz*=(0.5f*CNTLCYCLE);
74. qa=g_q0;
75. qb=g_q1;
76. qc=g_q2;
77. g_q0+=(-qb*gx-qc*gy-g_q3*gz);
78. g_q1+=(qa*gx+qc*gz-g_q3*gy);
79. g_q2+=(qa*gy-qb*gz+g_q3*gx);
80. g_q3+=(qa*gz+qb*gy-qc*gx);
82. //單位化四元數,意義在于單位化四元數在空間旋轉時是不會拉伸的,僅有旋轉角度.這類似與線性代數里面的正交變換
83. recipNorm=invSqrt(g_q0*g_q0+g_q1*g_q1+g_q2*g_q2+g_q3*g_q3);
84. g_q0*=recipNorm;
85. g_q1*=recipNorm;
86. g_q2*=recipNorm;
87. g_q3*=recipNorm;
89. //四元數到歐拉角轉換，轉換順序為Z-Y-X,參見.pdf一文,P24
90. //注意此時的轉換順序是1-2-3，即X-Y-Z。但是由于畫圖方便，作者這里做了一個轉換，即調換Z和X，所以順序沒變
91. g_Yaw=atan2(2*g_q1*g_q2+2*g_q0*g_q3,g_q1*g_q1+g_q0*g_q0-g_q3*g_q3-g_q2*g_q2)*180/PI;//Yaw
92. g_Roll=asin(-2*g_q1*g_q3+2*g_q0*g_q2)*180/PI;//Roll
93. g_Pitch=atan2(2*g_q2*g_q3+2*g_q0*g_q1,-2*g_q1*g_q1-2*g_q2*g_q2+1)*180/PI;//Pitch
94. }

注意其中的快速開方函數來自維基百科，精度0.175%。并且注意輸入的陀螺儀必須是弧度制(這一點在進入函數的時候已經做了轉換)，否則姿態解算是錯誤的。

針對上述代碼我還想說明一個筆者發現的問題：有很多網友和許多外國的四軸代碼(CrazyFlie)在這個姿態解算的加速度計部分都做了零點校準處理。意思就是在開機的時候讀取一定次數的加速度計的值，然后平均一下，得到一個初始狀態的偏移量，最后在輸出的時候加速度計減掉這個值，然后再給到姿態解算代碼部分。而筆者在剛開始移植代碼的時候是沒有做這個零點校準處理的(當然，陀螺儀必須要做零點處理，因為陀螺儀的原理，必須要在靜止時輸出為0)，包括現在依舊沒有對加速度計做零點校準處理，仍然可以獲得較為實時的姿態。