新型心跳呼吸模型的仿真設計原理及應用

0 引言

呼吸和心跳是維持人體正常新陳代謝和功能活動所必須的生理過程。在生命探測和醫學研究領域，都需要進行心跳呼模型的仿真。MAT-LAB是MathWorks公司于1982年推出的一款高性能的數值計算和可視化數學軟件。它可以用來求解各類學科問題，包括信號處理、圖象處理、神經網絡、控制系統辨識等。用MATLAB對心跳呼吸進行仿真，可以大大提高仿真工作效率。

1 生命信號特征分析

生命信號的規律性主要體現在心跳和呼吸的速率都很低。通常情況下，心跳次數約為每分鐘70到80次，即使是劇烈運動時，也不過130次左右；而呼吸引起的胸腔起伏通常約為每分鐘20到30次，呼吸急促時也不過是60次左右，所以，人體生命信號的探測，實際上就是低速運動目標的檢測。在人體情緒平穩時，心跳和呼吸的頻率基本維持在一個穩定的范圍內且呈周期性變化。

對于生命信號，很多情況下，也會呈現出非規律性。一般情況下，為了簡化分析，可以將人體目標信號假設成具有周期性頻率的正弦振蕩信號。而實際上，人體呼吸引起的胸腔運動以及心跳都不是正弦曲線。而且，由于人與人之間的差異，不同人的生命信號幅度和頻率等參數也是不同的。即使是同一個人，有些參數在不同的情況下也會發生變化。例如，人在受驚嚇時，呼吸就會加快，從而導致呼吸信號的幅度
和頻率升高。

2 跳呼吸模型仿真

2．1 正弦振蕩模型

通常情況下，在生命探測領域，心跳和呼吸模型可以用兩個正弦振蕩函數來表示：

其中，A1和A2分別為呼吸和心跳的振幅；w1和w2分別為呼吸和心跳的頻率；θ2是常數相位。

若將呼吸、心跳的頻率和幅度參數設置為：A1=0．4cm，A2=0．05cm，w1=1．57rad，w2=9．42rad，θ2=0．956。那么，由以上設定參數并通過matlab軟件所得出的心跳呼吸時域模型如圖1所示。

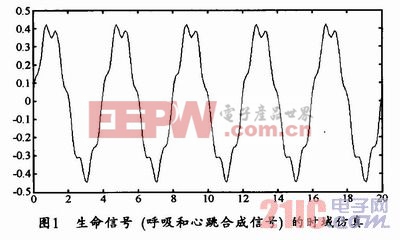
2．2 用最小二乘法對實測波型進行曲線擬合

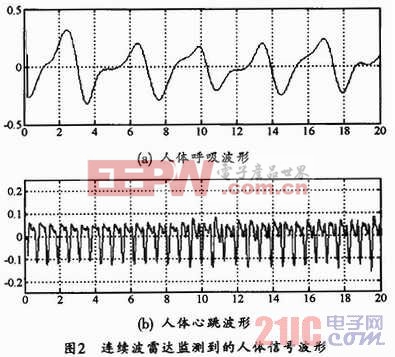
盡管人體的生命信號存在多樣性和差異性，然而，人體的生理特點決定了人體的呼吸、心跳活動具有一定的規律性。有時候，人們需要的心跳呼吸信號相對較為復雜，這時，就可根據實測波型進行模擬仿真。圖2所示是在自由空間內，用34GHz線性連續波生物雷達進行探測所得到的人體呼吸和心跳信號。

由圖2可以看出，連續波雷達監測到的人體心跳和呼吸波形在單個周期內均有兩個極大值和一個極小值。以心跳信號為例，在單個周期內，信號變化緩慢，波型上的拐點對應于人體心跳過程，可以用來作為標識心跳信號的特征點。其中，兩個極大值是由于心房、心室呈現周期性收縮、舒張所引起的。

根據連續波雷達監測到的人體呼吸的實測波形(即圖2(a))，在單個周期波形上選取能反映波形變化的特征點如下：

x1=[0 0．25 0．5 0．75 1 1．25 1．5 1．75 2 2．25 2．5 2．75 3 3．1]

y1=[-0．24 -0．23 -0．1 1 -0．01 0．03 0．015 0．1 0．2 0．29 0．315 0．24 0．1 -0．2 -0．26]；

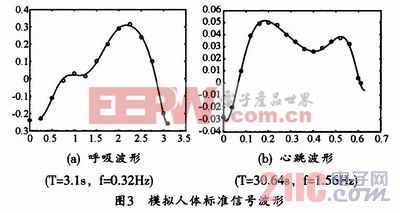
再用最小二乘法曲線擬合，并利用matlab軟件所得到的單周期人體標準呼吸波形如圖3(a)所示，圖中將其特征點用圓圈標出。

同理，根據圖2(b)也可取如下特征點：

x1=[0 0．04 0．08 0．12 0．16 0．2 0．24 0．28 0．32 0．36 0．4 0．44 0．48 0．52 0．56 0．6 0．61]；

y1=[-0．028 -0．02 0．01 0．039 0．049 0．05 0．048 0．04 0．034 0．028 0．026 0．029 0．034 0．037 0．032 0．004 0]；

同時也用最小二乘曲線擬合，所得到的單周期人體標準心跳波形如圖3(b)所示。

2．3 分段函數擬合模型

某些特殊試驗可能不方便或不能用前兩種方法來對心跳、呼吸模型進行仿真，這時可以采用分段函數擬合法來建立模型。心臟收縮、舒張一次需要的時間稱之為心動周期，正常的成年人的心動周期約為0．72秒。取振幅為0．04cm，周期為0．72s，可將心臟的收縮、舒張簡化為正弦分段函數：

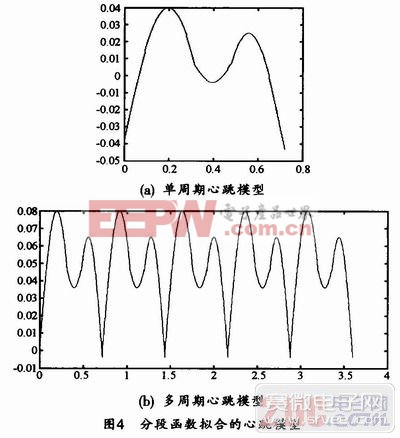
由式(2)得到的時域上的單周期和多周期心跳模型如圖4所示。

3 結束語

本文對人體的心跳、呼吸特征及規律進行了分析與研究，并針對不同需要給出了基于matlab軟件仿真的三種心跳、呼吸模型，包括正弦振動模型、最小二乘法對實測波型進行曲線擬合模型、及分段函數擬合模型。仿真結果證明，三種模型均符合理論分析及實際測量。本文對生命探測雷達、醫學、生理學等諸多科學的研究和具體工程應用均有一定的參考價值。