一種新的基于時域方法的EMC測試技術

本文討論了寬帶時域測量技術應用于測量電磁干擾(EMI) 時所具備的優勢。寬帶時域測量技術用于EMI測量時，其數字信號處理能力使它能夠實時仿真傳統模擬設備的各種測量模式，如峰值檢測模式、平均值檢測模式、 RMS檢測模式和類峰值檢測模式。同時，它還能引入諸如相位譜、短時譜、統計評估以及基于FFT的時－頻分析方法等新的分析理念。由于時域技術允許對整個信號譜內的幅度和相位信息進行并行處理，因此測量時間至少可以縮短一個數量級。本文還討論了該技術中用到的信號處理算法和利用時域電磁干擾系統(TDEMI)進行實際測量得到的測量結果。

隨著新技術的飛速發展，新的電子產品層出不窮。如何使電子產品滿足電磁兼容要求，并改善其電磁兼容性能，這已經成為產品開發過程中的一大難題。EMC和EMI測量設備能夠在較短的測量時間內提取大量精確的信息，采用這種設備能夠降低產品開發成本，并提高電路和系統開發的質量。一直以來，人們都是使用超外差射頻接收機[1][2]來測量射頻噪聲和電磁干擾(EMI)。這種方法的缺點是測量時間過長，對于30 MHz到1 GHz頻帶內的電磁干擾，通常需要測量30分鐘。測量時間過長就導致測試成本高昂，因此必須尋求一種能夠在不損失測量質量的前提下縮短測量時間的方法。傳統的測量系統并不評估被測EMI信號的相位信息，從而導致重要信息被丟失。而采用了傅立葉變換的EMI測量技術，其數字化處理就允許將時域內測量得到的信號分解成各種頻率成分。近幾年，隨著快速傅立葉變換(FFT)程序帶來的經濟效益日益明顯，FFT技術的應用已經快速普及起來。

本文討論了幾種新的信號處理方法，采用這幾種方法，時域測量技術能夠完成精確高效的EMI測量。此外，本文還介紹了為準確測量各種EMI信號而采用的信號處理策略。

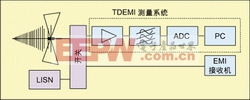
時域電磁干擾測量系統

圖1所示為一個時域測量裝置的框圖，其中包含一個時域電磁干擾(TDEMI)測量系統和一個用于與TDEMI做比較的傳統 EMI接收機。TDEMI系統中包含：寬帶天線(HL562, RohdeSchwarz)、線性阻抗穩定網絡(ESH 2-Z5, RohdeSchwarz)、開關單元(RSU, RohdeSchwarz)、放大器(ZFL-1000LN, Mini-Circuits)、低通濾波器(SLP-1000, Mini-Circuits)、模數轉換器(TDS7154, Tektronix, 示波器)和一臺個人計算機(兼容IBM)。文獻[3]中已經討論了TDEMI測量系統的硬件，該系統的工作基礎是對采樣后的EMI信號進行數字處理，其優點之一就是能夠通過軟件方式改善系統性能。

信號處理理論

ADC以采樣頻率fs 對輸入連續信號進行采樣和量化，相應的采樣間隔為1/fs = ?t。根據香農定理，fs至少應為信號最高頻率的兩倍。這一由采樣頻率決定的信號頻率上限也叫做奈奎斯特頻率。數字化之后，數據按N個樣本塊的形式送入估值程序，作為譜估計器的輸入。TDEMI系統中所采用的譜估計方法的數學基礎就是離散傅立葉變換(DFT)。對每一個數據塊進行的DFT變換定義如下：

DFT將離散時間信號序列x[n]變換為離散頻譜序列X[r]，其中n和r表示離散時間變量和離散頻率變量，并且n和r均為0到(N－1)之間的整數：

根據DFT的基本特性，?f 、N和 ?t之間滿足如下關系：

在頻譜X中，X[0]反映了信號的直流均值，而絕對值 則對應于在頻率標記為r處的合成矢量的幅度。要計算RMS值，必須將 中每個r > 1的元素均除以正弦信號的振幅因數 。而對應于奈奎斯特頻率的頻率標記R見下式：

由于一個實值信號經DFT變換后的絕對值是r的奇函數，因此信號的所有譜信息均包含在大于或小于奈奎斯特頻率的半邊X[r] 中。于是，后面的估值步驟只需要X[r]的一半就足夠了。信號能量在兩半頻譜中平均分布，因此必須將 的值乘以2才能準確地用單邊帶形式表示整個頻譜。要獲得與連續傅立葉變換類似的結果，DFT得到的譜值還必須進一步對時域樣本數N歸一化處理。下式定義了單邊幅度譜：

在實際的系統中，式(1)是通過快速傅立葉變換(FFT)實現的。為了避免當信號中包含非信號周期整數倍的周期成分時，頻譜泄漏至觀測時間內，應該加上一個窗函數。

窗函數在N/2處達到全局最大值，并向兩邊平滑滾降，在0和N-1處達到0，這樣就消除了對x[n]加窗時的邊沿效應。另一方面，加窗后的信號向量xW[n]所攜帶的能量比原始信號少，因為部分信號被削弱了。為了消除這一影響，我們限制窗函數序列，使其在觀測時間?TN內的積分等于1。w[n]的換算系數被稱作相關增益GC：

GC是一個換算系數，所以根據DFT的線性特性，GC可以與其他換算系數一起在頻域中進行譜變換之后使用。這樣，我們就得到了以下修正后的單邊幅度譜的定義公式：

不同的窗函數對頻率泄漏的抑制和頻譜分辨率二者的折衷程度不同。常用的窗函數有漢寧窗、漢明窗和平頂窗函數。