井斜測量系統中加速度計標定數據處理程序的設計

引言

在地質勘探中，為了確定地層側面傾角和傾斜方位角，必須連續測量井筒的傾角和傾斜方位角以及作為參考標志的井下儀器方位角。在進行鉆井或打水平井時需要知道井身軌跡和鉆頭位置，以調整下一步的鉆進方向。因此無論是完井之后或是在鉆井過程中，高精度且連續的井斜測量是必須的。

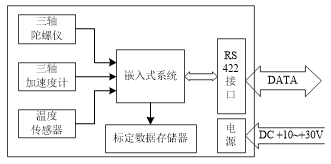
西安石油大學研制的xtcs(西安軌跡控制系統)，安裝了加速度傳感器來測量井下儀器運動姿態的井斜角（DEV）和工具面角(RB)。但是因為安裝的原因，即使精心調校，也不可避免地存在加速度傳感器的三軸不正交而引起的偏差，這個偏差對最后的測斜結果有不可忽視的影響，因此加速度傳感器在使用時要進行標定。

加速度計三軸不正交校正原理（Q校）

設{x}halfnote_{}^{→}、{y}halfnote_{}^{→} 、{z}halfnote_{}^{→}線性無關的三個向量，由它們可以構成一個空間坐標系，空間中的任何向量都可以表示成這三個向量的線性組合。從理論上可知，在空間坐標系中存在著一種單位正交坐標系，即構成坐標系的三向量相互垂直，其長度都等于1。空間任意坐標系和單位正交坐標系之間存在如下的對應關系：


Q值計算方法

由上可知，要進行傳感器校正，必須先確定Q值，通過準確測量傳感器的安裝位置來確定Q比較困難，而用計算的方法則簡單可行。已知重力加速度{G}halfnote_{}^{→}在正交坐標系中的三個分量是 G_{x}、G_{y}、G_{z}，反映儀器空間位置的幾個參數為井斜角（DEV）、工具面角(RB)和相對方位角(AZIM)（由于在傳感器中沒有加入磁強計，因此無法測量相對方位角，不予考慮）。其中井斜角和工具面角與 {G}halfnote_{}^{→}的關系為：

由于傳感器定位安裝方面的原因，實際測量的 G_{x}、G_{y}、G_{z} 是不正交的分量，為此需要用式（7）進行校正，然后才用式（8）和（9）確定儀器在井中的狀態。顯然，在不同的Q值下計算出的三個角度是不同的，它們都是Q的函數。

其中g是測量值，Q是待定系數，且g=(g_{x}g_{y}g_{z})^{T}， Q=(θ_{1}，θ_{2}，θ_{3})^{T}。由式（10）可知，任意給出一組Q值，便可計算出一組與測量值相對應的DEV,RB值。因此只要Q值選擇合適，就可以將軸不正交誤差減到最小，這個Q值就是我們希望得到的校正系數Q。
上述過程在數學上可表示為：

利用Matlab計算Q系數
Matlab是美國MathWorks公司開發的一個功能十分強大的高技術計算環境，是一種面向科學和工程計算的高級語言，它集科學計算、自動控制、信號處理、神經網絡、圖象處理等于一體，具有極高的編程效率。

Matlab目前有30多個工具箱，優化工具箱（Opuimization Toolbox）就是其中應用較廣泛、影響較大的一個。優化工具箱特點：無約束非線性函數的極小化問題；非線性最小二乘；非線性方程的求解；線性規劃；二次規劃；約束條件下非線性函數的極小化問題；非負線性最小二乘；極大極小多目標優化；半無窮極小化問題。Matlab具有強大的解決數值問題的能力及可擴充的環境，非常適合解決優化問題。

加速度傳感器標定數據處理軟件對目標函數的求解采用非線性最小二乘法進行曲線擬和，為了便于計算，在求解目標函數的過程中將工具面角的加權因子設為0，則目標函數就變為ΔDEV=sum_{}^{}(DEV-DEV_{0})^{2}，利用Matlab尋優工具箱中的非線性最小二乘擬和函數求解目標函數。下面簡單介紹一下用到的lsqonlin函數。

Lsqnonlin函數解決非線性最小二乘問題。
語法結構：x=lsqnolin(fun，x_{0})
1) 該函數處理的是非線性最小均方差問題，即：min{sum[FUN(x)2]},其中x為返回的值或矢量。
2) lsqonlin從x0的初值開始，最后到滿足函數FUN(x)均方誤差和最小的x值返回，也即在x處ΣFUN(x)2有最小值。

結論

在實驗室對加速度傳感器進行標定實驗獲得的數據，通過上述方法進行處理，得到Q校正處理和未校正處理計算的井斜角(DEV)和工具面角(RB)，對比如表1所示。傳感器標定數據經過不正交校正處理后井斜角和工具面角更接近真值，計算反映標定數據精確度的井斜角和工具面角的均方根誤差分別從0.32o、0.77o降低到0.12o、0.21o。

對于設計開發人員而言，眾多電氣組件接近所造成的"噪聲"環境，由此而產生的電磁兼容性（EMC）和電磁干擾（EMI）是他們關心的主要問題。為了應對這一設計挑戰，飛思卡爾半導體推出了可擴展微控制器（MCU）系列，幫助工程師降低大型家電和工業應用中的噪聲。