一種新的基于改進的ADALINE神經網絡的DTMF解碼器方

改進的ADALINE神經網絡采用LMS算法[2]，LMS算法本質是以最小均方誤差為準則的近似的最速下降算法。它以均方誤差為性能函數F(x)，定義如下

神經網絡的各個參數需要通過試驗來確定。經過試驗，對于DTMF檢測，選用只含有2個權系數和1個偏置值的網絡就可以勝任，也就是在圖4中，只需要w1/w2/b三個參數，結構簡單，計算量小。

對每個DTMF分量頻率都設置一個如圖4所示的神經網絡單元，在每個檢測周期對8個神經網絡單元的輸出進行判斷并簡單分析，就可以實現DTMF解碼。

四、基于改進的ADALINE神經網絡的DTMF解碼仿真結果

為了驗證上述基于改進的ADALINE神經網絡的DTMF檢測算法，我們在MATLAB上使用Neural Networks Toolbox進行了仿真。

仿真條件和參數選擇：模擬實際信道中常見的高斯白噪聲情況，待檢測輸入信號x(n)是DTMF信號和信道噪聲的疊加，輸入信噪比SNR是-3dB。為了討論方便，假定每個DTMF分量的幅度是+/-2V（只要進行比例縮放就可以適用實際情況），兩個分量信號幅度之和為+/-4V，并假定ADC接口之前的預處理電路的限幅電平是+/-5V，即兩個有用信號幅度之和占限幅電平的80%。改進的ADALINE神經網絡單元選擇含有2個權系數和1個偏置值，采用LMS算法，學習速度 選0.02。待檢測信號SNR=-3dB，采樣頻率為8KHz，采樣時間20ms。非線性環節的門限threshold選定為1.0V。

仿真結果如下：以*鍵為例，DTMF信號為941Hz/1209Hz。圖5上圖為純DTMF信號和高斯白噪聲信號，下圖為二者的疊加信號，即待檢測信號x(n)。

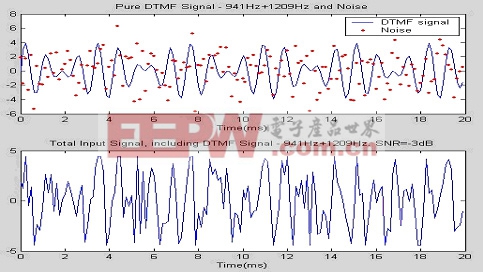圖5

圖6為對應941Hz的神經網絡單元的輸出，上圖為中間信號a(n)，下圖為網絡輸出信號y(n)。從圖中可以看出，網絡很快就能捕捉到輸入中的941Hz信號，輸出信號很強并且從12ms開始就基本穩定。因此系統判斷為輸入信號中含有941Hz的信號。對應1209Hz的神經網絡單元也類似。

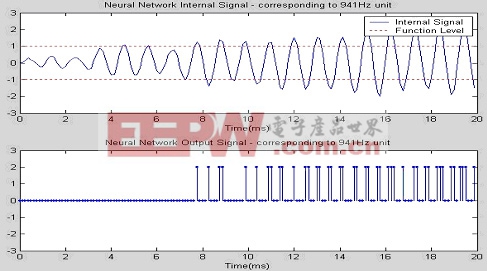圖6