自適應(yīng)在功率放大器非線性預(yù)失真中的應(yīng)用

在同一系統(tǒng)中，采用同樣的方法針對最陡下降法和LMS算法進行仿真，并與分段變步長算法的仿真結(jié)果進行比較，得到頻譜圖如圖4所示。

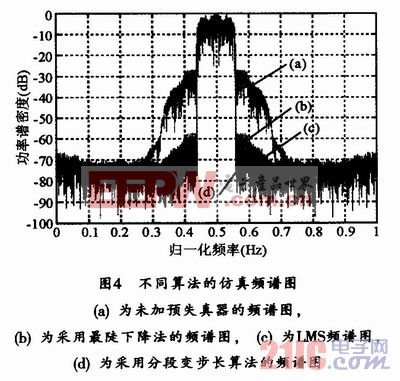
3．2 性能比較
采用歸一化均方誤差(NMSE)來表征計算的收斂速度和計算精度，其表達式為

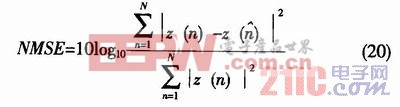
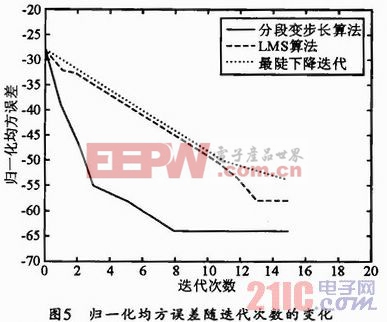
每迭代一次，按上式求出NMSE的值并記錄，三種自適應(yīng)算法得到的仿真結(jié)果如圖5所示，分段變步長算法的迭代次數(shù)明顯少于最陡下降法及LMS算法。

采用誤差矢量幅度(EVM表征帶內(nèi)失真，相鄰信道功率比ACPR表征帶外失真。

其中，s(f)為功率譜密度， [f1，f2]為傳輸信道，[f3，f4]為相鄰信道。
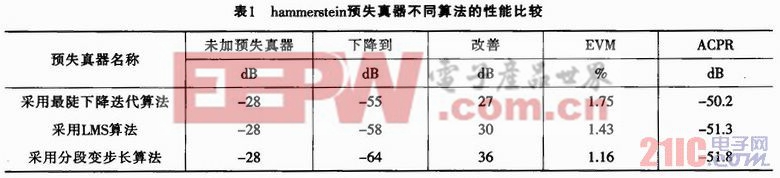
按照(21)與(22)兩式分別計算最陡下降法、LMS算法及分段變步長算法，得到結(jié)果如表1所列。

4 結(jié)束語
本文采用Wiener模型作為功率放大器，與之相逆的hammerstein模型作為預(yù)失真器，用間接學(xué)習(xí)的預(yù)失真方法，采用三種不同的自適應(yīng)算法最陡下降法、LMS算法、分段變步長算法進行系統(tǒng)仿真比較，通過matlab仿真結(jié)果表明，分段變步長自適應(yīng)算法不僅在收斂速度(迭代次數(shù))上明顯優(yōu)于其他兩種自適應(yīng)算法，并在帶內(nèi)失真與帶外失真較之其他兩種算法也有明顯改善。