基于GC5016的并行多通道接收機研究

由于CIC濾波器的通帶傾斜較大，信號通過CIC濾波器之后，頻譜會產(chǎn)生一定的傾斜，且伴有較大損耗，所以后端的PFIR濾波器在繼續(xù)對信號進行抽取降速的基礎上，還要對信號進行一定程度的補償，以便抵消CIC濾波器的通帶傾斜。
3．2 PFIR濾波器
用一個已知的窗函數(shù)ω(k)去截取一個理想濾波器的沖激函數(shù)hid(k)，就能得到一個實際可用的FIR濾波器沖擊函數(shù)h(k)，即窗函數(shù)法，這是最簡單、最常用的設計FIR濾波器的方法。常用的窗函數(shù)ω(k)有矩形窗、漢寧窗、海明窗、布-哈窗(Blackman-Harris)以及凱撒(Kaise r)窗等。除此之外，還有等波紋最佳一致逼近法(Parks-Mcclellan最優(yōu)法)及頻域采樣法等。
FIR濾波器的階數(shù)即窗函數(shù)長度是由濾波器的實際需求決定的，對于某些類型的窗函數(shù)，給定δp，δs，fC，fA等濾波器參數(shù)就可確定所需的濾波器階數(shù)。例如對凱撒窗，當δ=δp=δs時，則N由下式給出：

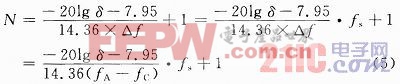
式中：△f，fC，fA分別為實際模擬帶寬和頻率值；fs為采樣頻率。由上式可見，數(shù)字濾波器的階數(shù)N與濾波器的歸一化過渡帶寬度成反比，與濾波器帶內(nèi)波動的對數(shù)值成正比，過渡帶越窄帶內(nèi)波動越小，所需的濾波器階數(shù)越大，實現(xiàn)起來也越困難，所以實際應用中，需要對
三者進行權(quán)衡折衷。目前有很多商用濾波器設計軟件包可供選擇，Matlab的信號處理和濾波器設計工具箱，提供了強大的設計和仿真功能。本文使用Matlab對GC5016的濾波器設計進行了仿真。

4 仿真及結(jié)果
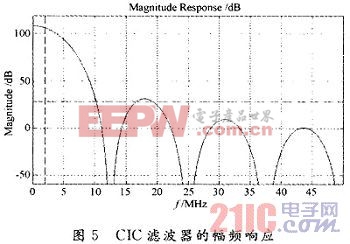
仿真實用Matlab的濾波器設計工具箱，假設抽取因子M=8，差分延時D=1，信號通帶為2 MHz，阻帶衰減Ast為80 dB，采樣率fs為100MHz，則CIC濾波器的幅頻響應如圖5所示。