基于Multisim的負電阻特性分析及應用

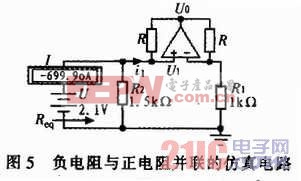
圖5所示為負電阻與正電阻的并聯連接，根據圖形可得式(12)，并推導出并聯等效電阻為式(13)。


可見，負電阻與正電阻并聯的等效電阻仍然滿足兩個正電阻的并聯關系式1／R=1／R1+1／R2。等效電阻可正可負，取決于R1和R2的大小。由式(10)可以看出，正負電阻并聯時，要求R1≠R2。
負電阻與正電阻并聯，運算放大器工作于線性區的條件為：|u|R1Usat／(R+R1)。
圖3所示的電路，其等效電阻的理論值為
(-1 kx1．5 k)／(-1 k+1．5 k)=-3 k
仿真結果為2．1 V／(-699．9μA)=-3 k
2．3 負電阻與正電阻的混聯
含負電阻的電阻們串并聯，其等效電阻可以按照正電阻的串并聯等效方法進行計算。
圖6所示的電路，-R1與R2并聯后再與R3串聯，最后與-R4并聯。

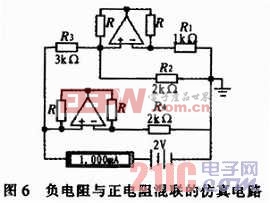
等效電阻的理論值為
[-1 k∥2 k)+3 k]∥(-2 k)=2 k
仿真結果為2 V／(1 mA)=2 k

3 負電阻的應用實例
負電阻十分有用，如在電源設計中可用負電阻中和不需要的正電阻，形成理想電源；在有源濾波器和振蕩器設計中，負電阻可用來控制極點的位置；電位器串一個負電阻就能擴大變阻范圍，在負值與正值之間任意調節，等等。
例如，在研究R、L、C串聯電路的方波響應時，由于電感元件本身存在直流電阻rL，方波電源也具有內阻，因此，響應類型只能觀察到過阻尼R>2sqrt(L／C)、臨界阻尼R=2sqrt(L／C)和欠阻尼R2sqrt(L／C)三種形式。
利用負電阻構成具有負內阻的方波電源作為激勵，使電源的負內阻和電感器的電阻相“抵消”，則回路總電阻就可出現零值和負值的情況，即響應類型可以出現無阻尼等幅振蕩情況和負阻尼發散振蕩情況。
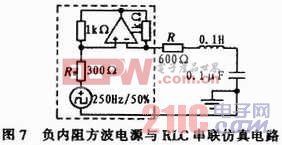
圖7所示，虛框內是具有負內阻的方波電源，調節Rs或R的值，改變回路的總電阻值，在總阻值接近零和達到負阻值時，便可觀察到無阻尼等幅振蕩響應和負阻尼發散振蕩響應。本文用multisim的參數掃描功能，將Rs設為600 Ω和700 Ω，對uc進行瞬態分析，uc的初始狀態和瞬態時間范圍分別設為0V和0～2 ms，設置完畢，點擊對話框右上方的Simulate仿真按鈕，就可得到圖8所示的uc的等幅振蕩曲線和發散振蕩曲線。

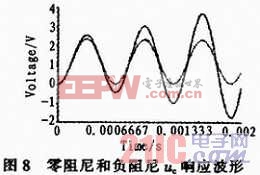
4 結論
理論推導和Multisim仿真實驗的結果說明：用正電阻與運算放大器進行搭建而成的負電阻具有負阻值特性，得出了在存在負電阻的電阻串并聯等效變換中，負電阻的處理方法與正電阻一致的結論。在電源設計時，可用這樣的負電阻中和不需要的正電阻，形成理想電源；在有源濾波器和振蕩器設計中，可用這樣的負電阻來控制極點位置，得到理想的結果等。這樣的負電阻在理論分析和實際應用中都具有重要作用。