電壓型PWM整流器電感下限值設(shè)計(jì)與分析
摘要:從電壓型PWM整流器(VSR)網(wǎng)側(cè)輸入正弦電流在過零點(diǎn)處電流脈動量最大特點(diǎn)出發(fā),詳細(xì)分析了電流過零處一個(gè)PWM采樣周期內(nèi)電流脈動量與各開關(guān)導(dǎo)通時(shí)間、電源頻率、系統(tǒng)電感值、電網(wǎng)電壓、功率給定及輸出直流電壓的關(guān)系,設(shè)計(jì)了VSR交流側(cè)電抗器最小值。在Saber仿真平臺上進(jìn)行了仿真實(shí)驗(yàn),得到了不同電感值下系統(tǒng)輸出直流電壓、輸入電流的變化波形,結(jié)果驗(yàn)證了該設(shè)計(jì)方法的正確性和可行性。
關(guān)鍵詞:整流器;電抗器設(shè)計(jì);電流脈動量;最大輸出功率
1 引言
PWM整流器以其交、直流側(cè)可控的4象限運(yùn)行方式,可控制網(wǎng)側(cè)電流及功率因數(shù)的特點(diǎn),逐漸成為電力電子領(lǐng)域的研究熱點(diǎn)。目前,對于PWM整流器的研究熱點(diǎn)集中在控制策略的研究方面,對系統(tǒng)主電路參數(shù)設(shè)計(jì)的研究較少。在三相VSR的設(shè)計(jì)中,網(wǎng)側(cè)電感參數(shù)的確定至關(guān)重要。功率電路設(shè)計(jì)的好壞也是三相VSR系統(tǒng)能否正常及進(jìn)一步實(shí)用化的關(guān)鍵,三相VSR網(wǎng)側(cè)電感對三相VSR系統(tǒng)的影響是綜合性的,其取值不僅影響系統(tǒng)的動、靜態(tài)性能,而且還會對三相VSR的額定輸出功率等其他因素產(chǎn)生影響。增大電感值,可抑制系統(tǒng)輸入電流的諧波,減小整流器的使用所造成的電網(wǎng)污染。但系統(tǒng)提供給負(fù)載的最大功率就會下降;減小電感值,可提高系統(tǒng)響應(yīng)速度及系統(tǒng)輸出功率,但輸入電流的脈動量會變大,造成系統(tǒng)輸入電流諧波增加。
因此,正確選取系統(tǒng)交流側(cè)電抗器值對系統(tǒng)而言具有重要意義。文獻(xiàn)提出了一些計(jì)算方法,但結(jié)果均不理想。在此從VSR網(wǎng)側(cè)輸入正弦電流在過零點(diǎn)處電流脈動量最大特點(diǎn)出發(fā),詳細(xì)地分析了在電流過零處一個(gè)PWM采樣周期內(nèi)電流脈動量與各開關(guān)導(dǎo)通時(shí)間、電源頻率、系統(tǒng)電感值、電網(wǎng)電壓、功率給定及輸出直流電壓的關(guān)系,設(shè)計(jì)了VSR交流側(cè)電抗器最小值。在仿真平臺上進(jìn)行了仿真,得到了不同電感值情況下系統(tǒng)輸出直流電壓、輸入電流的變化波形,結(jié)果驗(yàn)證了該設(shè)計(jì)方法的正確性和可行性。
2 基于開關(guān)函數(shù)的三相VSR系統(tǒng)模型
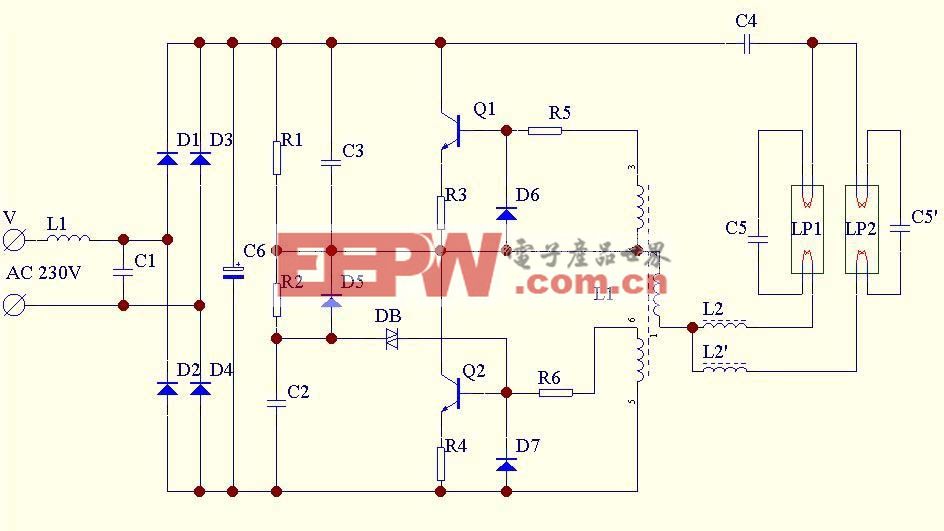
三相VSR主電路結(jié)構(gòu)如圖1所示。Lre為網(wǎng)側(cè)濾波電感,即所需設(shè)計(jì)的對象。根據(jù)基爾霍夫電壓定律有:Lredik/dt=ek-ikRrem-uk+uo,k=a,b,c。
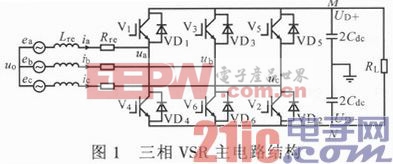
由于三相VSR系統(tǒng)無中線,且電網(wǎng)輸入平衡,將直流電容的中點(diǎn)作為系統(tǒng)參考地時(shí),網(wǎng)側(cè)三相電源中心點(diǎn)電壓值為:uo=(ua+ub+uc)/3。將其代入Lredik/dt=ek-ikRre-uk+uo可得:
Lredik/dt=ek-ikRre-uk+(ua+ub+uc)/3 (1)
其中,對三相VSR的整流橋開關(guān)信號S作如下定義:當(dāng)Sk=1時(shí),上管導(dǎo)通,下管關(guān)斷;當(dāng)Sk=0時(shí),下管導(dǎo)通,上管關(guān)斷。根據(jù)主電路結(jié)構(gòu)形式,直流側(cè)電壓與整流橋網(wǎng)側(cè)輸入電壓間存在如下關(guān)系:uk=SkUD+(1-Sk)UD-。將上式代入式(1),則:
Lredik/dt=ek+(-3Sk+Sa+Sb+Sc)Udc/3 (2)
3 基于輸入電流脈動量的電感最小值設(shè)計(jì)
三相VSR在運(yùn)行中,電流脈動量較大處就是在電流過零和峰值處,其中過零點(diǎn)處電流脈動量最大。下面以限制輸入電流最大脈動量為目的來設(shè)計(jì)電感,以a相為例,討論電感設(shè)計(jì)。圖2為a相電流在過零處,一個(gè)采樣周期內(nèi)a相電流和開關(guān)信號的對應(yīng)波形。
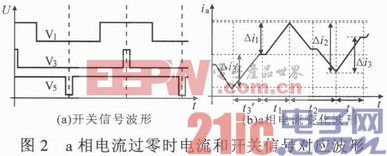
根據(jù)圖2所示,依據(jù)電壓空間矢量脈寬調(diào)制(SVPWM)方法,此時(shí)給定電壓矢量處于第VI扇區(qū),即處于a相過零附近。如果忽略零矢量的作用,則:t1=t3=T1/2,t2=T2,T1,T2為非零矢量作用時(shí)間。則在(ωt,ωt+t1],(ωt+t1,ωt+t1+t2],(ωt+t1+t2,ωt+Tcs]內(nèi),根據(jù)式(2)分別可得:

pwm相關(guān)文章:pwm是什么
pwm相關(guān)文章:pwm原理
電抗器相關(guān)文章:電抗器原理 脈寬調(diào)制相關(guān)文章:脈寬調(diào)制原理 矢量控制相關(guān)文章:矢量控制原理




評論