基于三相四線APF的模糊直接反饋控制

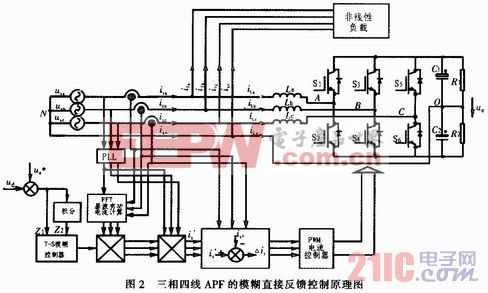
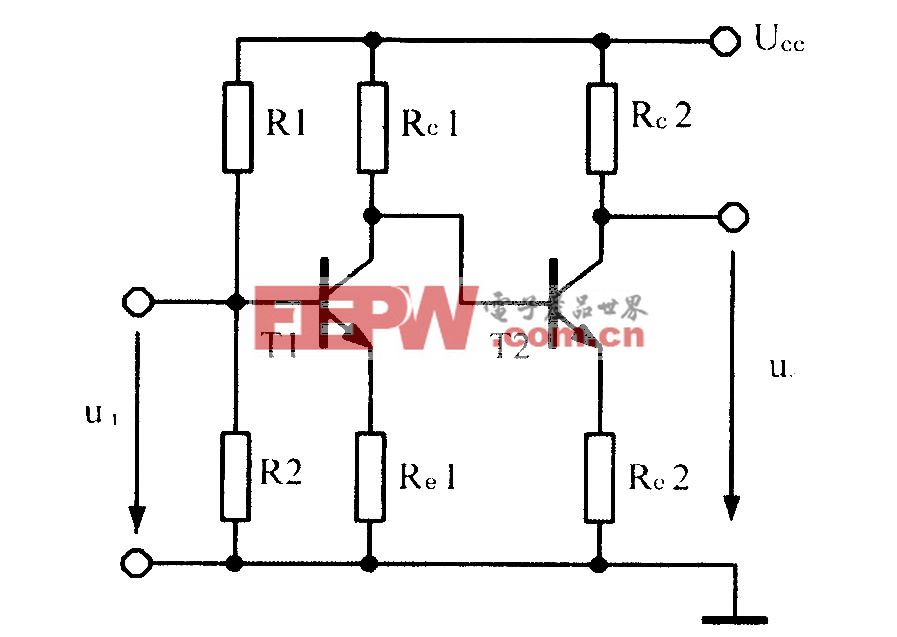
經由以上的分析,將模糊控制器構造閉環反饋控制,可以對三相四線APF的進行有效地控制,校正了由負載非線性電流,實現了對非線性電流的補償,實現的原理如圖2所示。本文引用地址:http://www.104case.com/article/160466.htm
3 模糊反饋控制器設計
3.1 三相四線APF的T-S模糊直接反饋控制穩定性
對于以上所建立三相四線APF的T-S模糊控制模型(17),利用平行分布補償算法設計模糊狀態反饋控制律(18),得到閉環反饋控制系統(19),需要保證系統是穩定的。對開環模糊模型(17)在狀態反饋控制律(18)條件下的閉環模糊系統(19),存在一個公共的對稱正定矩陣H,和矩陣Gij=Mi-NiKj,選取Lyapunov函數V(x(t))=xδ(t)THxδ(t),當x(t)≠0時,有V(x(t))0。根據Lyapunov穩定定理,閉環模糊系統(19)在平衡點是全局漸近穩定的。
3.2 三相四線APF的T-S模糊直接反饋控制器設計
為了求解模糊反饋控制器的狀態反饋增益矩陣Ki及正定矩陣H,通過簡單的變量代換,轉換為求解等價的矩陣X=H-1及矩陣Yi=KiX的線性矩陣不等式形式,可通過MATLAB軟件中的LMI工具箱求解。本系統中,三相四線APF的主電路參數為La=Lb=Lc=L=4 mH,C1=C2=4700μF,R1=R2= 5 kΩ,根據主電路模型,參考文獻,選擇x4(0)=800 V,得平衡點處da(0)=0.111 25,db(0)=dc(0)=0.694 375,x1(0)=-0.137 2 A,x2(0)=x3(0)=0.068 6 A。

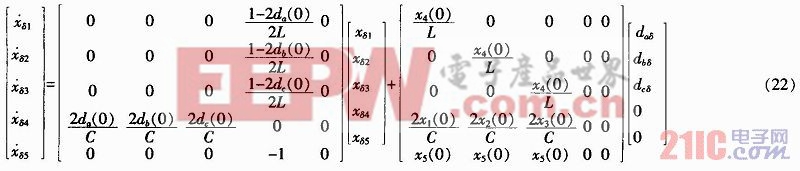
故系統在平衡點處的狀態空間模型如式(22)所示。
由式(15)和式(16)的模糊前件變量函數,可得到系數矩陣行列式Mi、Ni的數值解。根據系統的特性,選擇α1=10,α2=80,利用LMI工具箱可得到公共正定矩陣H以及4個反饋增益矩陣K1,K2,K3和K4的數值解。
4 仿真及實驗結果
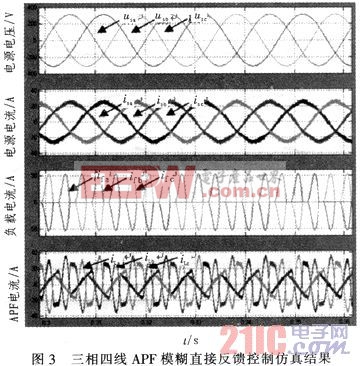
由以上分析,在MATLAB中建立如圖2所示的三相四線APF模糊直接反饋控制的仿真電路。其中三相非線性負載為三相全橋整流電路,濾波電感為0.5 mH,濾波電容為1 000μF,負載電阻為25 Ω,仿真結果如圖3所示。











評論