RBF神經網絡在智能傳感器模塊設計中的應用

RBF神經網絡Matlab源程序

RBF神經網絡Matlab源程序如下：

clc

clear

close all %程序開始前，清屏，清除其它變量

%輸入原始數據，每一列為一個變量，行數為樣本的個數。原始標定數據的輸入，可以將數據直接輸入至程序中，也可以將數據先輸入至文件，然后在程序中讀入數據文件。數據中的P、Ut、Ui、Up均為維列向量， 為標定數據點的個數

raw_data=[P Ut Ui Up]； %學習（訓練）樣本

data_test=[P_test Ut_test Ui_test Up_test]； %測試樣本

%根據原始數據制作學習（訓練）樣本與測試樣本，學習樣本與測試樣本的數據格式相同

P=raw_data(: , 1); Ui=raw_data(: , 2); Ut=raw_data(: , 3); Up=raw_data(: , 4);

P_test=data_test(: , 1); Ui=data_test(: , 2); Ut=data_test(: , 3); Up=data_test(: , 4);

P1= ; [Up Ui Ut] %學習樣本輸入

T1= ; P' %學習樣本期望輸出

P2= ;[Up_test Ui _test Ut_t est]' %測試樣本輸入

T2=P_test' ； %測試樣本輸出

%將輸入數據進行歸一化

[PN1，Minp，maxp，TN1，mint，maxt]=premnmx(P1，T1)；

PN2=tramnmx(P2，minp，maxp)；

TN2=tramnmx(T2,mint,maxt);

%訓練

switch 2

case 1 %神經元數是訓練樣本個數

spread=0.1； %此值越大，覆蓋的函數數值就越大（默認為1）

net=newrbe(PN1，TN1，spread)；

case 2 %神經元數逐步增加，最多就是訓練樣本個數

goal=1e－8； %訓練誤差的平方和（默認為0）

spread=0.1； %此值越大，需要的神經元就越少（默認為1）

MN=size(PN1,2)； %最大神經元數（默認為訓練樣本個數）

DF=2； %顯示間隔（默認為25）

net=newrb(PN1，TN1，goal，spread，MN，DF);

case 3

spread=0.1； %此值越大，需要的神經元就越少（默認為1）

net=newgrnn(PN1，TN1，spread);

end

%測試

YN1=sim(net，PN1)； %學習（訓練）樣本實際輸出

YN2=sim(net，PN2)； %測試樣本實際輸出

MSE1=mean((TN1－YN1).ˆ2 %學習（訓練）樣本實際輸出的均方誤差

%n1=length(TN1)；%e1=sum((TN1－YN1).ˆ2/n1

%e1與MSE1相等

MSETD1=std((TN1－YN1).ˆ2

MSE2=mean((TN2－YN2).ˆ2 %測試樣本實際輸出均方誤差

%n2=length(TN2)；%e2=sum((TN2－YN2).ˆ2/n2

%e2與MSE2相等

MSETD2=std((TN2－YN2).ˆ2

%反歸一化

Y1=postmnmx (YN1,mint,maxt)' %將歸一化的學習（訓練）輸出數據恢復為原始數據

E1=Y1－P %學習（訓練）輸出數據與標定值之間的偏差

Y2=postmnmx (YN2,mint,maxt)' %將歸一化的測試輸出數據恢復為原始數據

E2=Y2－P_test %測試輸出數據與標定值之間的偏差

max(E2)

min(E2)

采用經過數據歸一化處理的程序

神經網絡采用Matlab中的newrb()函數，neurons=252。學習樣本經RBF神經網絡訓練后的輸出值與相應的壓力標定值之間的最大誤差絕對值為1.0396e－011，均方誤差MSE1=5.6613e－023，均方誤差的標準差MSETD1=2.4666e－022。這里省略學習樣本的預測輸出表。可見，采用RBF神經網絡對學習樣本的輸出已經消除了壓力傳感器的交叉敏感影響（在誤差允許的范圍內）。

檢驗樣本經RBF神經網絡的輸出值與相應的壓力標定值之間最大偏差絕對值為max=0.0113，均方誤差MSE2=3.8568e－005，均方誤差的標準差MSETD2=2.1727e－004。輸出樣本的詳細情況見表5（只列出部分數據）。

數據融合效果評價

降低溫度與電源波動兩個干擾量的影響，傳感器系統穩定性的改善程度分別用融合前后的零位、靈敏度溫度系數以及電流影響系數來評價。

由于學習（訓練）樣本的網絡輸出值與標定值之間的偏差很小（均小于1.0e－011），如果根據這些數據來計算融合后的效果，可以認為已經完全消除交叉敏感。通過表5可知，本例中檢驗樣本的網絡輸出值與標定值之間的偏差與學習樣本的偏差相比，偏差較大，故按檢驗樣本計算出數值來評價數據融合效果。

表5 輸出樣本

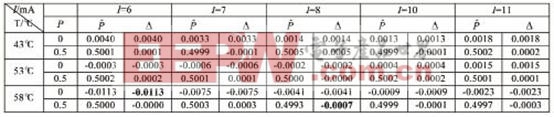
注：表中T表示工作溫度，I表示工作電流，P表示壓力標定值，表示壓力計算值，偏差，單位都是V。

融合前：滿量程輸出值UFS=4.928V，當溫度的變化范圍為=39℃（由25℃至64℃），電流由6mA至11mA，變動時，零點值的最大變化范圍=0.356V（由0.328V至-0.028V），滿量程輸出值由4.928V下降到2.710V，輸出變化范圍=-2.218V。

（1）零位溫度系數

（2）靈敏度溫度系數

（3）電流影響系數

利用檢驗樣本計算的融合后的零位溫度系數、靈敏度溫度系數以及電流影響系數如下：

在=39℃，變化范圍內，零點融合計算值的最大偏差 =0.0113MPa；滿量程壓力PFS=0.5MPa，其融合計算值的最大偏差量=0.0007MPa，則有

將融合前和RBF神經網絡融合后的各參數列于表6中。

表6 融合前和RBF神經網絡融合后的各參數

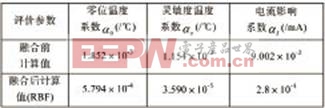
從表6可見，經RBF神經網絡融合后，零位溫度系數降低到融合前的1/3，靈敏度溫度系數降低約3個數量級，電流影響系數降低約2個數量級

結束語

由于半導體的特性參數易受溫度、電流的影響而變化，壓阻式傳感器將會產生很大的零位溫度漂移、靈敏度溫度漂移和電流影響漂移，這是壓阻式傳感器最大的弱點。因此，研究改善壓阻式壓力傳感器的溫度穩定性與恒流源供電電流的穩定性，在生產實踐中很有意義。采用RBF神經網絡法，設計了抗兩個干擾量影響的智能化軟件模塊，對壓阻式壓力傳感器穩定性進行改善，取得了很好的效果。該方法簡單易行，精度較高，將壓阻式壓力傳感器輸出精度控制在0.01%以內。